Table of Contents

• Introduction to small scale physics and unavoidable randomness
  • Temperature
  • Diffusion
  • Limited energy scale of ATP
  • Stochasticity of reaction kinetics
• A simple ratchet model for myosin
• Kinetics of two-state models
• Kinesin-Dynein Tug-of-War

Introduction

(More advanced students way want to skip ahead and get going with myosin motor proteins.)

Why and what do cells need to move?

• Subcellular Compents
  • What are important things cells need to move around inside themselves?
• Themselves
  • When is it important for cells to be able to move?
  • When do cells need to change their shape or grow in certain directions?
• You!
  • What has to happen on the cellular level to make your muscles move?

Discuss: How do you think cells do this?

What might make it hard for cells to generate motion?

Randomness of being at a small scale

First: What is temperature?

It's more than just hot and cold, and there is a precise scientific definition.

Discuss: How would you define temperture?

Temperature is a measure of disorder and random motion in a system. To be precise, it is proportional to the average energy per degree of freedom. (A degree of freedom just is a way the system can be moving randomly. For example, there are three translational, three rotational, and a few vibrational degrees of freedom per molecule for most small molecules). In a cell this can be thought of in terms of water molecules bouncing off of each other and causing the proteins and everything they bump into to also bounce and wiggle around randomly.

Problem: At temperature T, each degree of freedom has an average of \(\frac{1}{2}k_BT\) of energy where \(k_B = 1.38*10^{-23}\text{J}/\text{K}\) is the Boltzmann Constant. There are three translational degrees of freedom (x, y, and z), and each water molecule has a mass of \(3*10^{-26}\text{kg}\). If all the energy in the translational degrees of freedom were kinetic energy, what would be the (root-mean-square) average velocity of water molecules at \(300^\circ\text{K}\)? Does this surprise you?

(In reality this number is smaller by about a factor of 10 because most of that energy goes into the potential energy created by water molecules bumping into each other. And, the water molecules don't actually travel that far because they are constantly bumping into each other and bouncing around the same small volumes. Nevertheless, this gives a sense of how much random energy and motion there is at this scale!)

See a definition of temperature!

Diffusion

When left alone in the random motion of water, small particles will drift around randomly. This is called diffusion.

Diffusion obeys the equation \(\frac{\partial p(x,t)}{\partial t}=D\nabla^2p(x,t)\). For a known starting position \(p(x,0)=\delta(x,0)\) this has the solution:

\(p(x,t)=\frac{1}{\sqrt{2\pi(2Dt)}}e^{-x^2/(2(2Dt))}\)

This is a normal distribution with \(\sigma=2Dt\).

Problem for students with calculus: Prove that this is a solution to diffusion equation and that \(p(x,0)=\delta(x,0)\) for this solution.

What is the diffusion constant \(D\)? The diffusion constant is given by the Einstein equation: \(D=\mu k_BT\) where \(\mu\) is the mobility, which in a viscous medium is the ratio of the particle's velocity to the resulting drag force: \(\mu=v/F_d\). For a spherical particle \(\mu=1/(6\pi\eta R)\) where \(\eta\) is the fluid viscosity and for water is approximately \(\eta_{\text{H}_2\text{O}}=10^{-3}\text{ Pa s}=10^{-3}\text{ pN}/(\text{um}^2/\text{s})\).

The Einstein equation can be derived by the following argument: The time-evolution for the probability distribution for a particle is given by \(\frac{\partial}{\partial t}p(x,t)=-\mu F\frac{\partial}{\partial x}p(x,t)+D\frac{\partial^2}{\partial x^2}p(x,t)\). At equilibrium \(\frac{\partial}{\partial t}p(x,t)=0\). There is also an important result from statistical physics know as the Boltzmann distribution, which states that at equilibrium: \(p(x)\propto e^{-U(x)/k_BT}\). Plugging this in and relating the force to the potential energy gradient will yield the Eistein equation.

Problem for students with calculus: Plug in and simply the resulting equation to complete this derivation.

Problem: Introducing a force \(F\) shifts the mean of the normal distribution for a particle's position according to \(\left< x\right>=\mu Ft\). Calculate the time at which this value becomes larger than two standard deviations of the probability distribution for the particle's position. This corresponds to the time at which the particle has a 97.5% chance of having made net-progress in the direction it is being pulled. Assume a spherical partical of radius \(R\) and express your answer in terms of \(\eta\).

Energy Scale of ATP

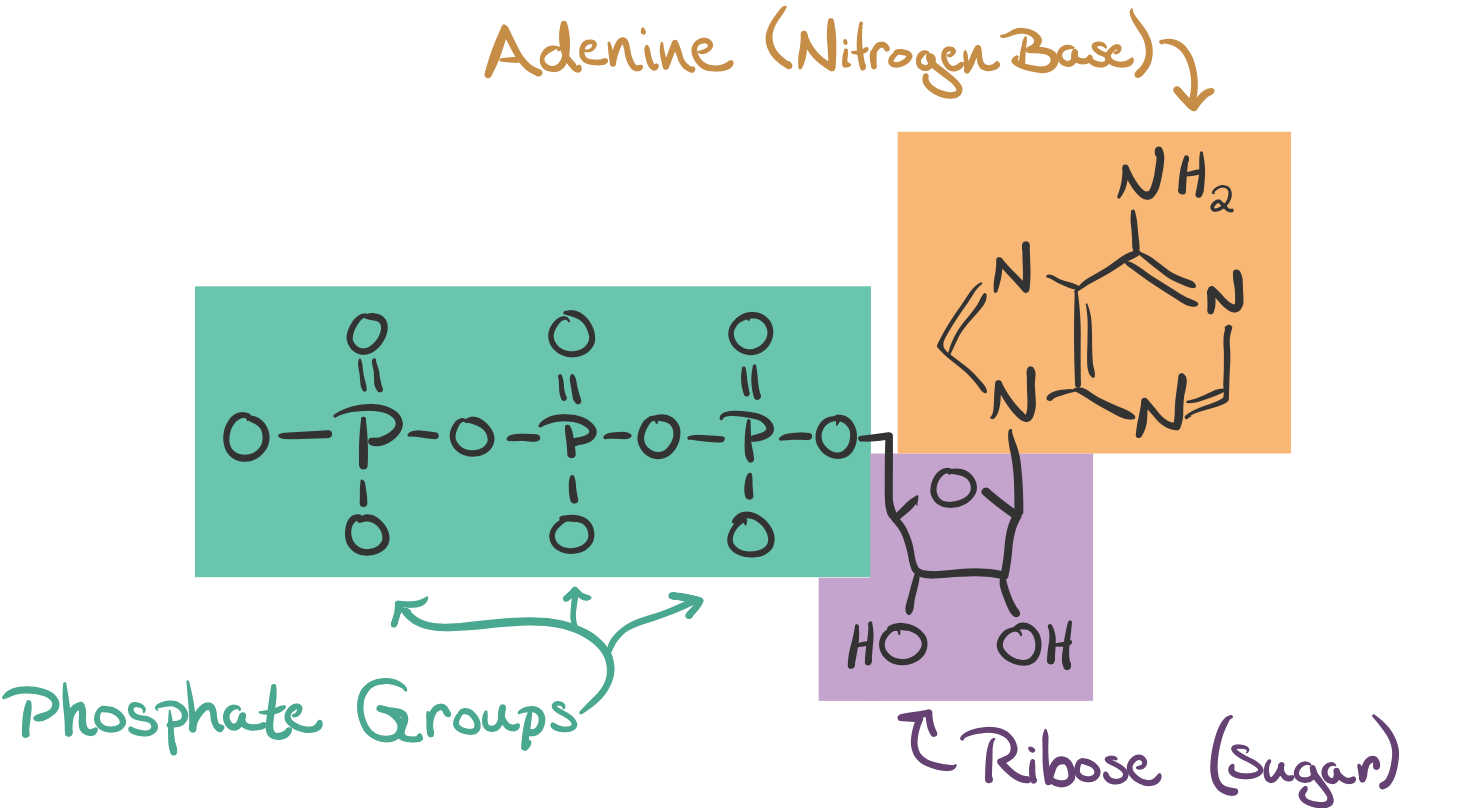
The main "energy currency" of cells is ATP, a small molecule consisting of a three phosphates. When a cell consumes sugars, fats, and other energy sources, it mostly produces ATP. Most proteins in the cell

Under typical cellular conditions, hydrolysis of ATP to ADP yeilds around \(30\text{ kJ}\) (kiloJoules) of energy per mole of ATP. This is \(0.05\text{ aJ}\) (attoJoules) \(=5*10^{-20}\text{ J} = 50 \text{ pN nm}\) (picoNewton-nanometer) of energy per ATP molecule.

Problem: Using the results of the previous problem, calculate the average amount of work that must be done to move an object an average distance that is twice the standard deviation associated with the diffusion of the particle during the same period of time. How does this compare to the energy scale of ATP? Use a temperature of \(300^\circ\text{K}\).

Problem: Assuming 100% efficiency, how many ATP molecules does it take to lift a 1 kg textbook 1 meter off the ground?

Problem: What is the ratio of the free energy available from one molecule of ATP to the thermal kinetic energy of a protein with three translational, three rotational, and no vibrational degrees of freedom? Does this seem like a lot?

Stochasticity of Chemical Reactions and State Changes

In the same way that particles diffuse rather than move deterministically, chemical reactions and changes to the internal states of proteins do not behaive deterministically. A chemical reaction, for example, always has a reverse reaction. One direction can be made significantly more favorable than the other direction but this requires the products to have a lower free energy than the reactants. If a series of chemical reactions are to proceed in a repeating cycle, one of the steps most undo the decreases in free energy of the other steps. When the contribution from all the different steps get brought together, a closed loop of reactions cannot be favored to proceed in one direction over the other direction. Because changes to internal states of proteins are essentially just chemical reactions the same restriction apply. For these reason small-scale systems can often be better thought of in terms of different states with set free energies and transition probabilities that depend on those free energies

Biology gets around this limitation by coupling reactions to ATP hydrolysis, which provides a source of free energy. Because ATP only provides a limited amount of energy, a reaction cycle that consumes one ATP per cycle must spread the free energy consumption out across all its state transitions. The free energy released by ATP hydrolysis is only a few times large than the inherent scales of stochasticity in biological systems. In order for a reaction cycle to run smoothly there must be no step that significantly rate-limits the whole cycle, this requires spreading the free energy consumption out across all the reaction steps (usually by hydrolyzing ATP to reach a high-free energy state and then slowly stepping down in free energy for the rest of the cycle). This also implies that cycles with relatively few states will run most smoothly because each step can have a more sizeable free energy decrease.

Myosin and other Molecular Motors

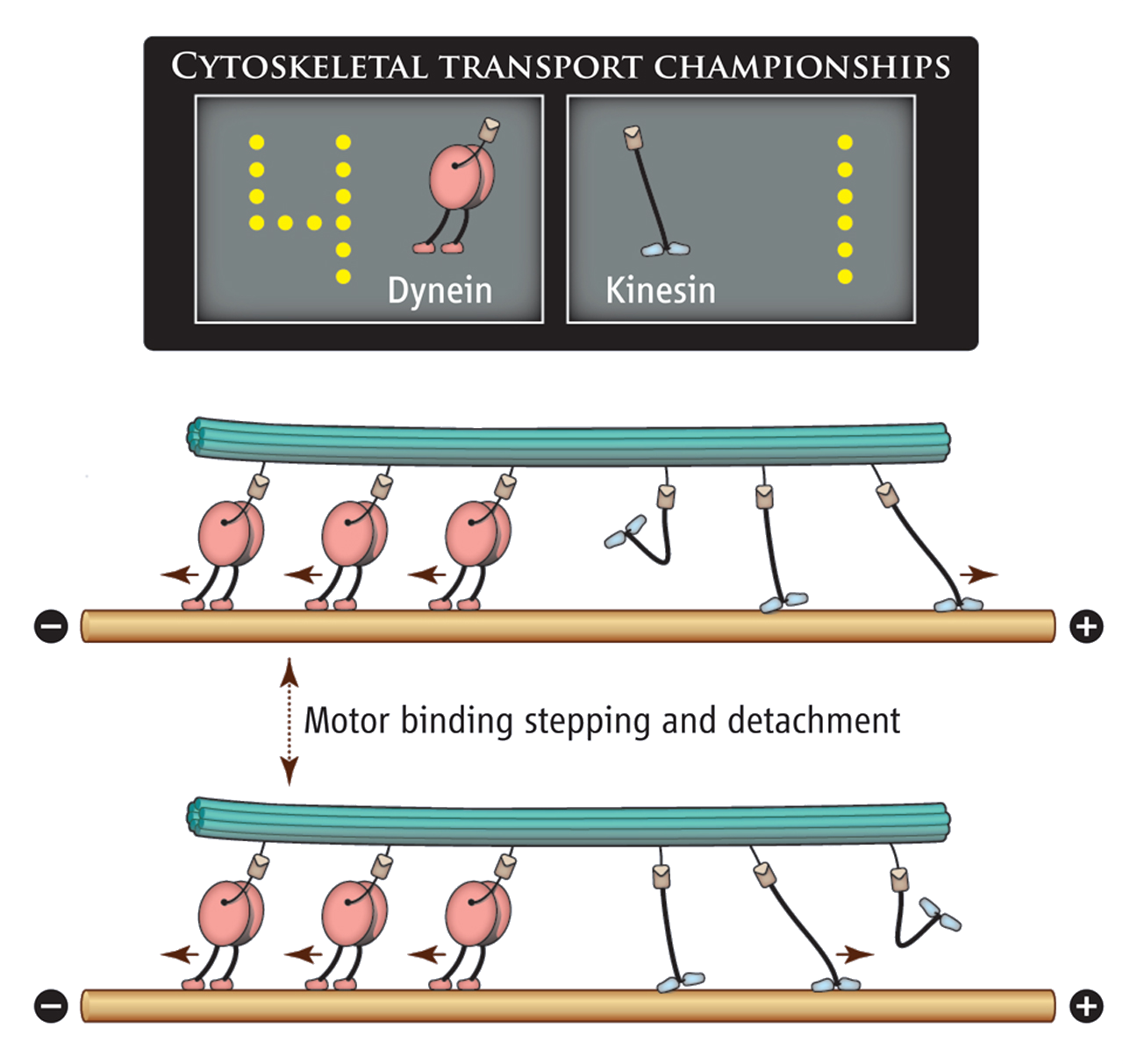
Myosin is one of the most common motor proteins in cells and is used for transporting sub-cellular components, making muscles contract, and maintaining the cells physical/mechanical structure. Myosin travels on long polymer filament known as actin. Myosin has several varieties, some with one head that detaches and reattaches as it moves down the actin filament, some with two heads that function like a pair of feet, and some that are found in bundles with several heads all working together. Dynein and kinesin are two other common motor protein. They walk on slightly large microtubules and always exist with two heads. Dynein and kinesin actually walk in different directions on microtubules, which produces some interested dynamics that we will explore below. The motor protein shown on the right is kinesin walking on a microtubule.

Recall the challenges for molecular motors. There is inherent random on small scales. Diffusion nearly overshadows an movement a single ATP hydrolysis could produce. Chemical reaction and state changes happen stochastically with probability depending on the free energies of the different states. Motions are simple and any practical cycle must only have a limited number of states.

Discuss: Some motor proteins can actually harness random motion to create a net-forward motion. How might they do this?

See a model for harnessing random motion!

Two-State Ratchet Model

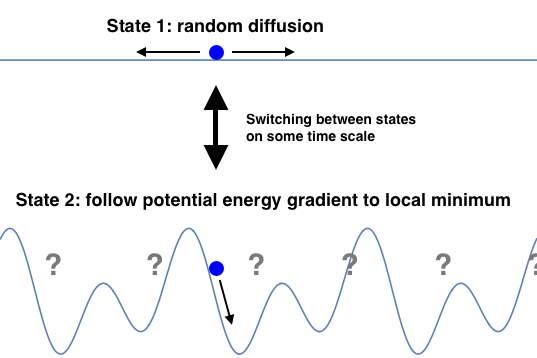
A two state motor switches between two states with different potential energy functions U(x). In the simplest case, one state has a flat potential and corresponds to the motor freely diffusing (with equal probability of moving forwards or backwards). The other state has a periodically repeating potential whose gradient the motor protein follows to a local minimum. In order for this model to work ATP (or another free energy source) must be consumed to break a symmetry that will be explored in the next section.

Myosin is very commonly described using this model as are other molecular motors.

Discuss: If you were to design the second potential energy function to maximize forward motion, what would it look like? You need to capture and ideally amplify any forward diffusion while rejecting any backwards diffusion.

See the potential energy function in the two-state ratchet model for myosin!

Myosin Sawtooth Ratchet

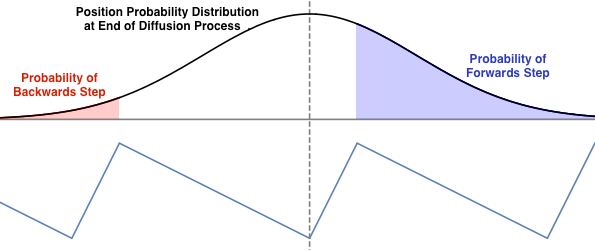
The sawtooth ratchet uses a potential energy function that pulls the moter protein head towards the front of whichever well it reattaches to. Being closer to the well one forwards than to the previous well makes the particle more likely end up in the next well and take a step forward than a step backwards on the next diffusion step.

Discuss: This model still has two free parameters: the location of the potential energy minimum relative to the two peaks and the width of the normal distribution for the diffusion process (which is related to how long the myosin head diffuses for). What choices of these parameters maximize the frequency of forward steps and minimize the frequency of backwards steps? What is the maximum possible frequency of forward steps?

Discuss: If you could also design a (non-flat) potential energy function for the diffusive process, what frequency of forward step could you obtain?

Problem for students with calculus: Using a diffusion constant of \(1\ \mu\text{m}^2/\text{s}\), a spatial period of 70 nm, and a potential energy minimum 20 nm behind the next potential energy maximum, calculate the optimal time for the diffusion step to maximize forward motion. You can use a tool such as wolframalpha.com to help with the integrals and derivatives.

Kinetics of the Two-State Model

(This section involves mostly calculations. Students with less advanced math backgrounds or without experience with chemical kinetics or statistical mechanics might want to skip ahead to Kinesin-Dynein Tug-of-Wars.)

Here we will use a simple model of a motor protein to demonstrate why ATP hydrolysis is necessary for a two-state model to work.

In our model, the motor protein has a repeating series of two states \(\{A_i,B_i\}\) with each pair of states cooresponding to some position along its filament. The protein can move between states \(A_i\) and \(B_i\) and between states \(B_i\) and \(A_{i+1}\) (but not directly between states \(A_i\) and \(A_{i+1}\)).

\(\ldots \leftrightarrow A_{i-1} \leftrightarrow B_{i-1} \leftrightarrow A_{i} \leftrightarrow B_{i} \leftrightarrow A_{i+1} \leftrightarrow B_{i+1} \leftrightarrow \ldots\)

We can define the forward rates to be \(v_1\) and \(v_2\) and the backwards rates to be \(u_1\) and \(u_2\):

\(A_i\xrightarrow{v_1}B_i\xrightarrow{v_2}A_{i+1}\)

\(A_i\xleftarrow{u_1}B_i\xleftarrow{u_2}A_{i+1}\)

We assign each state a free energy (\(G_A\) and \(G_B\)) and also define energy barriers: \(G^\dagger_1\) between states \(A_i\) and \(B_i\) and \(G^\dagger_2\) between \(B_i\) and \(A_{i+1}\). Reaction kinetics (essentially the single-molecule equivalents of what you might have learned in AP Chemistry), now tell us that:

\(v_1=c_1e^{-(G^\dagger_1-G_A)/k_BT}\quad\quad v_2=c_2e^{-(G^\dagger_2-G_B)/k_BT}\)

\(u_1=c_1e^{-(G^\dagger_1-G_B)/k_BT}\quad\quad u_2=c_2e^{-(G^\dagger_2-G_A)/k_BT}\)

Problem: Prove that there can be no net forward motion in this model.

In order to overcome this limitation, motor proteins hydrolyze ATP. If this is done between states \(A_i\) and \(B_i\), the change in free energy associated with moving from state \(A_i\) to \(B_i\) gains a term of the change in free energy associated with hydrolysing ATP: \(\Delta G_\text{ATP}\). So \(v_1\) becomes:

\(v_1=c_1e^{-(G^\dagger_1-G_A-\Delta G_\text{ATP})/k_BT}\)

This breaks the symmetry that previously resulted in no net forward progress. This results can be easily generalized to the case of an arbitary number of states \(\{A_i,B_i,C_i\ldots\}\) with any pattern of pathways between them and the \(i-1\) and \(i+1\) states using the basic properties of chemical equilibria.

Of course, this model doesn't explicitly capture the spatial component of the ratchet model. To look at this case, we instead consider a slow enough transition between bound and dispersing states such that when in the bound state the position of the myosin can be considering to be in a thermodynamic equilibrium within its potential well. Statistical physics tells us that the equilibrium position probability distribution of the myosin in the bound state is given by:

\(p(x)\propto e^{-U(x)/k_BT}\)

We can further assume a constant potential energy \(U_\text{disp}>\text{max}[U(x)]\) for the dispersive state and assume the rate of enter the dispersive state when at position \(x\) is given by:

\(v_{\text{bound}\rightarrow\text{disp}}(x)\propto e^{-(U_\text{float}-U(x))/k_BT}\)

Problem: Prove that the probability distribution for the myosin's position when it enters the dispersive state is uniform and independent of \(U(x)\).

With a uniformly distributed starting position for dispersive state neither forward nor backwards step are more likely because the tails of the position probability distribution at the end of the dispersive step extend equal into the \(i+1\) and \(i-1\) regions.

Kinesin-Dynein Tug-of-War

Kinesin and dynein are two motor proteins that both walk on microtubules. Kinesin moves towards the "plus" end of the microtubule and dynein towards the "minus". Because they move in opposite directions, it is possible for them to engage in a tug-of-war if they are attached to the same cargo. The maximum force from a single kinesin is 7 pN and the maximum force from a single dynein is 5 pN. Which do you expect to win in tug-of-war with an equal number of kinesin and dynein?

It turns out dynein wins and that even just one or two dynein can win against half a dozen kinesin.

Discuss: Why might dynein so easily win a tug of war against kinesin?

See why dynein wins

Dynein wins because kinesin has a lower "processivity" to microtubules, meaning that even though kinesin will pull hard when attached it easily falls off the microtubule. Kinesin becomes increasingly likely to fall off the microtubule as the force it is pulling against increases. The simplest model of this force-processivity relationship is:

\(r_\text{off}=r_0e^{F/F_0}\)

The force \(F\) is the per kinesin force of the dyneins pulling against the kinesins, so:

\(F=\frac{(5\text{ pN})(N_\text{dyn})}{N_\text{kin,att}}\)

The rate for a kinesin reconnecting to the microtubule can be kept as a constant \(r_\text{on}\).

These rate are for each individual kinesins. The velocities for the total population of \(N\) kinesins, \(N_\text{att}\) of which are attached are:

\(v_\text{off}=N_\text{att}r_0e^{F/F_0}\quad\quad v_\text{on}=(N-N_\text{att})r_\text{on}\)

We will consider the case of 2 dyneins and 10 kinesins and use \(F_0=2\text{ pN}\), \(r_\text{on}=1\text{ ms}^{-1}\), and \(r_0=(1/4)r_\text{on}\). It is worth noting that with this choice of \(r_0\), kinesin would be attached to its microtubule 80% of the time.

Problem: Calculate \(v_\text{on}\), \(v_\text{off}\), and \(v_\text{on}-v_\text{off}\) at \(N_\text{att}=\{1,2,4,6,8,9\}\). What does this tell you about the number of kinesins one would expect to be attached? Is there a single value the systems converges towards? Pay attention to the sign of \(v_\text{on}-v_\text{off}\) at different values of \(N_\text{att}\).

See solution

\(\quad N_\text{att}\quad \)	\(\quad v_\text{on}\quad \)	\(\quad v_\text{off}\quad \)	\(\quad (v_\text{on}-v_\text{off})\quad \)
1	9	37	-28
2	8	6.1	1.9
4	6	3.5	2.5
6	4	3.5	0.5
8	2	3.7	-1.7
9	1	3.9	-2.9

This system displays what is known as bistability. If there is just one kinesin attached it most likely detaches before a second kinesin attaches. If, however, two kinesins become attached then a third, fouth, and eventually seventh are likely to attach.

If we had tried this calculation with fewer eight kinesin, we would not have found any positive values of \((v_\text{on}-v_\text{off})\), which means the system will also trend toward all kinesin detaching. This demonstrates how two dynein can win out against several kinesin in this simple model.