To find the solution at the end of a given increment a set of nonlinear
equations has to be solved. In order to do so, the Newton-Raphson method is
applied, i.e. the set of equations is locally linearized and solved. If the
solution does not satisfy the original nonlinear equations, the latter are
again linearized at the new solution. This procedure is repeated until the
solution satisfies the original nonlinear equations within a certain
margin. Suppose iteration ![]() has been performed and convergence is to be
checked. Let us introduce the following quantities:
has been performed and convergence is to be
checked. Let us introduce the following quantities:
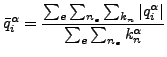 |
(154) |
where ![]() represents all elements,
represents all elements, ![]() all nodes belonging to a given
element,
all nodes belonging to a given
element, ![]() all degrees of freedom for field
all degrees of freedom for field ![]() belonging to a given
node and
belonging to a given
node and
![]() is the flux for a given degree of freedom of field
is the flux for a given degree of freedom of field
![]() in a given node belonging to a given element at the end of iteration
in a given node belonging to a given element at the end of iteration
![]() . Right now, there are two kind of fluxes in CalculiX: the force for mechanical calculations
and the concentrated heat flux for thermal calculations.
. Right now, there are two kind of fluxes in CalculiX: the force for mechanical calculations
and the concentrated heat flux for thermal calculations.
| (155) |
where ![]() denotes the change due to iteration
denotes the change due to iteration ![]() .
.
| (156) |
where ![]() denotes the change due to the present increment. In mechanical
calculations the solution is the displacement, in thermal calculations it is
the temperature.
denotes the change due to the present increment. In mechanical
calculations the solution is the displacement, in thermal calculations it is
the temperature.
| (157) |
Now, two constants ![]() and
and ![]() are introduced:
are introduced: ![]() is used to check
convergence of the flux,
is used to check
convergence of the flux, ![]() serves to check convergence of the
solution. Their values depend on whether zero flux conditions prevail or
not. Zero flux is defined by
serves to check convergence of the
solution. Their values depend on whether zero flux conditions prevail or
not. Zero flux is defined by
| (158) |
The following rules apply:
The values in square brackets are the default values. They can be changed by using the keyword card *CONTROLS. Now, convergence is obtained if
| (159) |
AND if, for thermal or thermomechanical calculations (*HEAT TRANSFER, *COUPLED TEMPERATURE-DISPLACEMENT or *UNCOUPLED TEMPERATURE-DISPLACEMENT), the temperature change does not exceed DELTMX,
AND at least one of the following conditions is satisfied:
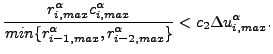 |
(160) |
If convergence is reached, and the size of the increments is not fixed by the user (no parameter DIRECT on the *STATIC, *DYNAMIC or *HEAT TRANSFER card) the size of the next increment is changed under certain circumstances:
If no convergence is reached in iteration ![]() , the following actions are
taken:
, the following actions are
taken:
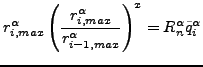 |
(161) |
from which ![]() can be determined. Now, if
can be determined. Now, if
![$\displaystyle i+\frac{\ln \left( R_n^\alpha \frac{\tilde{q}^{\alpha}_i}{r^{\alp...
...\ln \left( \frac{r^{\alpha}_{i,max}}{r^{\alpha}_{i-1,max}} \right) } > I_C [16]$](img866.png) |
(162) |
(which means that the estimated number of iterations needed to reach
convergence exceeds ![]() ) OR
) OR ![]() , the increment size is adapted according to
, the increment size is adapted according to
![]() and the iteration of the increment is restarted unless
the parameter DIRECT was selected. In the latter case the increment is not
restarted and the iterations continue.
and the iteration of the increment is restarted unless
the parameter DIRECT was selected. In the latter case the increment is not
restarted and the iterations continue.