Frequency calculations

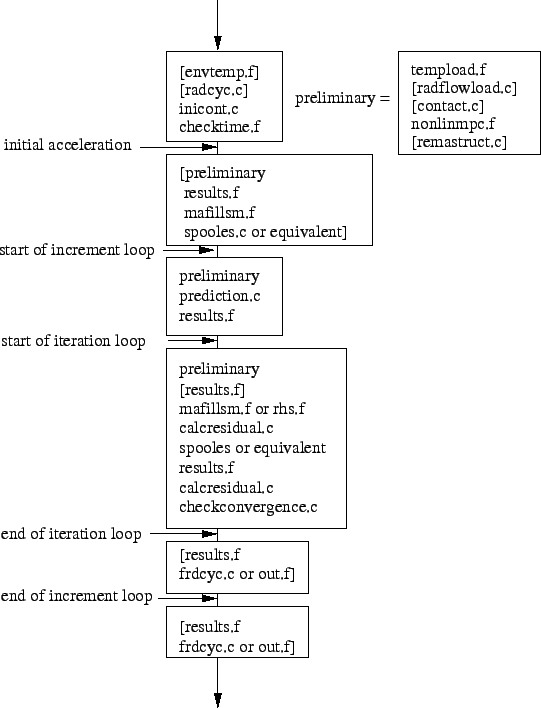
Frequency calculations are performed in subroutines arpack.c for structures not exhibiting cyclic symmetry and arpackcs.c for cyclic symmetric structures. Frequency calculations involve the following steps:

• filling the stiffness and mass matrix in mafillsm.f. The stiffness matrix depends on the perturbation parameter: if iperturb=1 the stress stiffness and large deformation stiffness of the most recent static step is taken into account ([17])
• solving the eigenvalue system using SPOOLES and ARPACK
• calculating the field variables in results.f, including storing in the .dat file
• storing the results in .frd format in out.f

The eigenvalues and eigenmodes are solved in shift-invert mode. This corresponds to Mode 3 in ARPACK ([38]). Suppose we want to solve the system

$$\begin{bmatrix}K \end{bmatrix} \begin{Bmatrix}U \end{Bmatrix} = \omega^2 \begin{bmatrix}M \end{bmatrix} \begin{Bmatrix}U \end{Bmatrix}$$ (210)

then the shift-invert mode requires algorithms for solving

$$\begin{bmatrix}K - \sigma M \end{bmatrix} \begin{Bmatrix}U \end{Bmatrix} = \begin{Bmatrix}X_1 \end{Bmatrix}$$ (211)

and for calculating

$$\begin{Bmatrix}Y \end{Bmatrix} = \begin{bmatrix}M \end{bmatrix} \begin{Bmatrix}X_2 \end{Bmatrix}$$ (212)

where $\begin{Bmatrix}X_1 \end{Bmatrix}$ and $\begin{Bmatrix}X_2 \end{Bmatrix}$ are given and $\sigma$ is a parameter. In CalculiX, it is set to 1. These operations are used in an iterative procedure in order to determine the eigenvalues and the eigenmodes. For the first operation SPOOLES is used. SPOOLES solves a system by using a LU decomposition. This decomposition is performed before the iteration loop initiated by ARPACK since the left hand side of Equation (211) is always the same. Only the backwards substitution is inside the loop. The second operation (Equation (212)) is performed in routine op.f and is a simple matrix multiplication. Notice that this routine depends on the storage scheme of the matrix.

For cyclic symmetric structures the following additional tasks must be performed:

• Expanding the structure in case more than one segment is selected for output purposes (parameter NGRAPH on the *CYCLIC SYMMETRY MODEL keywork card). This is done before the mafillsm call.
• Calculating the results for the extra sectors based on the results for the basis sector. This is performed after the call of routine results.f.