Thermodynamics and Propulsion

5.3 Combined First and Second Law Expressions

The first law, written in a form that is always true:

$$dU =dQ -dW.$$

For reversible processes only, work or heat may be rewritten as

$$dW=PdV,$$

$$dQ=TdS.$$

Substitution leads to other forms of the first law true for reversible processes only:

$$dU=dQ-\underline{PdV}, \textrm{ substituted for a reversible }dW$$

$$dU=\underline{TdS}-dW, \textrm{ substituted for a reversible }dQ.$$

(If the substance has other work modes, e.g., stress, strain,

$$dU =dQ -PdV -XdY,$$

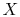where $X$ is a pressure-like quantity, and 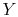$Y$ is a volume-like quantity.)

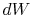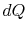Substituting for both $dW$ and $dQ$ in terms of state variables,

$$dU =TdS -PdV \qquad\textrm{Always true.}$$

The above is always true because it is a relation between properties and is now independent of process.

In terms of specific quantities:

$$du =Tds -Pdv \qquad\textbf{Combined first and second law (a) or Gibbs equation (a).}$$

The combined first and second law expressions are often more usefully written in terms of the enthalpy, or specific enthalpy, $h = u + Pv$ ,

$$dh =\underline{du}+Pdv+vdP$$

$$=\underline{Tds -Pdv} +Pdv + vdP,\textrm{ using the first law.}$$

$$dh =Tds + vdP.$$

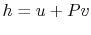Or, since $v = 1/\rho$ ,

$$dh=Tds + \frac{dP}{\rho} \qquad\textbf{Combined first and second law (b) or Gibbs equation (b).}$$

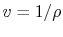In terms of enthalpy (rather than specific enthalpy) the relation is

$$dH =TdS +VdP.$$