Just as Chap. 4 was initiated with the representation of an
irrotational vector field E, this chapter began by focusing on the
solenoidal character of the magnetic flux density. Thus,  o H
was portrayed as the curl of another vector, the
vector potential A.
o H
was portrayed as the curl of another vector, the
vector potential A.
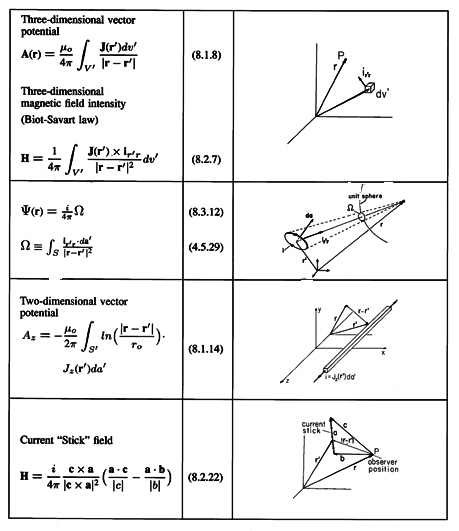
The determination of the magnetic field intensity, given the current density everywhere, was pursued first using the vector potential. The integration of the vector Poisson's equation for A was the first of many exploitations of analogies between EQS and MQS descriptions. In Cartesian coordinates, the superposition integral for A, (8.1.8) in Table 8.7.1, has components that are analogous to the scalar potential superposition integral, (4.5.3), from Table 4.9.1. Similarly, the two-dimensional superposition integral, (8.1.14), has as its analog (4.5.20) from Table 4.9.l.
Especially if a computer is to be used, it is often most practical to work directly with the magnetic field intensity. The Biot-Savart law, (8.2.7) in Table 8.7.1, gives H directly as an integration over the given distribution of current density.
In many applications, the current distribution can be approximated by piece-wise continuous straight-line segments. In this case, the total field is conveniently represented by the superposition of contributions given by (8.2.22) in Table 8.7.1 due to the individual "sticks."
In regions free of current density, H is not only solenoidal,
but also irrotational. Thus, like the electric field intensity of
Chap. 4, it can be represented by a scalar potential  , H
= -
, H
= - 
 . The magnetic scalar potential is, in general,
discontinuous across a surface carrying a surface current density.
It is its normal derivative that is continuous. The scalar potential
provides an elegant representation of the fields in free space
regions surrounding current loops. The superposition integral,
(8.3.12) in Table 8.7.1, is written in terms of the solid angle
. The magnetic scalar potential is, in general,
discontinuous across a surface carrying a surface current density.
It is its normal derivative that is continuous. The scalar potential
provides an elegant representation of the fields in free space
regions surrounding current loops. The superposition integral,
(8.3.12) in Table 8.7.1, is written in terms of the solid angle
 .
.
Through the combined effects of Faraday's law, flux continuity, and Ohm's law, currents are induced in a conductor by a time-varying magnetic field. In a perfect conductor, these currents are on the surface, distributed in such a way as to shield the magnetic field out of the conductor. As a result, the normal component of the magnetic flux density must be zero on the surface of a perfect conductor.
Although useful for representing any solenoidal field, the vector
potential is especially useful in the situations summarized by Table
8.7.2. It is especially convenient for describing systems with
perfectly conducting boundaries.
In two dimensions, the boundary condition on a perfect conductor
is satisfied by making the vector potential constant on the boundary.
The approaches of Chaps. 4 and 5 apply equally well to solving MQS
boundary value problems involving perfect conductors. In fact, the
two-dimensional EQS and MQS configurations of perfect conductors in
free space, exemplified by the configurations of Figs. 4.7.2 and 8.6.7,
were found to be duals. Formally, the solution for H follows
from that for E by identifying 
 Az,
Az,  /
/ o
o 
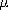 o Jz. However, while the
electric field intensity E is perpendicular to the surfaces of
constant
o Jz. However, while the
electric field intensity E is perpendicular to the surfaces of
constant 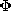 , H is tangential to the surfaces of constant
Az.
, H is tangential to the surfaces of constant
Az.
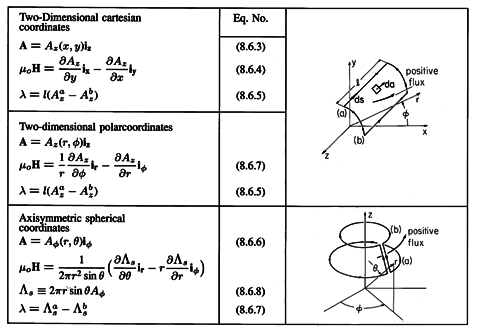
The boundary conditions obeyed by the vector potential at surfaces of discontinuity (containing surface currents) reflect the discontinuity in tangential H field and the continuity of the normal flux density. The vector potential itself must be continuous (a discontinuity of A would imply an infinite H in the surface)

where Ampère's continuity condition

requires that curl A have discontinuous tangential components.
The condition that A be continuous, (1), guarantees the
continuity of the normal flux density. [According to (1), the
integral of A  ds around an incremental closed contour
lying on one side of the surface is equal to that on the other.
Thus, the normal flux which each of these integrals represents, is
the same as well.]
ds around an incremental closed contour
lying on one side of the surface is equal to that on the other.
Thus, the normal flux which each of these integrals represents, is
the same as well.]
In fluid mechanics, the scalar Az would be called a
"stream-function", because in two dimensions, lines of constant vector
potential constitute the flux lines. In axisymmetric configurations,
the flux lines are lines of constant 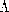 s, as defined in Table
8.7.2.
Of course, a similar representation can be used for any solenoidal
vector. For example, an expression for the two-dimensional lines of
electric field intensity in a region free of charge density could be
obtained by finding a vector potential representation of E.
Thus, in these special cases, the vector potential is convenient for
plotting any solenoidal field.
s, as defined in Table
8.7.2.
Of course, a similar representation can be used for any solenoidal
vector. For example, an expression for the two-dimensional lines of
electric field intensity in a region free of charge density could be
obtained by finding a vector potential representation of E.
Thus, in these special cases, the vector potential is convenient for
plotting any solenoidal field.
The electric potential 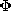 of EQS systems, evaluated on the
surface of a perfectly conducting capacitor electrode, can be used to
evaluate the terminal voltage. The vector potential is similarly
related to the terminal characteristics of a lumped parameter
element, this time an inductor. Indeed, we found in Sec. 8.6 that
the flux per unit length linked by a pair of conductors in two
dimensions was simply the difference of vector potentials evaluated
on the two conductors. In Sec. 8.4, we found that the terminal
voltage is the time rate of change of this flux linkage.
of EQS systems, evaluated on the
surface of a perfectly conducting capacitor electrode, can be used to
evaluate the terminal voltage. The vector potential is similarly
related to the terminal characteristics of a lumped parameter
element, this time an inductor. Indeed, we found in Sec. 8.6 that
the flux per unit length linked by a pair of conductors in two
dimensions was simply the difference of vector potentials evaluated
on the two conductors. In Sec. 8.4, we found that the terminal
voltage is the time rate of change of this flux linkage.
The division of the field into particular and homogeneous parts makes possible a number of different approaches to obtaining the total field. The particular part can be obtained using the vector potential, using the Biot-Savart law, or by superimposing the fields of thin coils represented in terms the scalar magnetic potential. The homogeneous solution is both irrotational and solenoidal, so it is possible to use either the vector or the scalar potential to represent this part of the field everywhere. The vector potential helps determine the net flux, as required for calculating the inductance, but is of limited usefulness for three-dimensional configurations. The scalar potential does not directly portray the net flux, but does generally apply to three-dimensional configurations.

