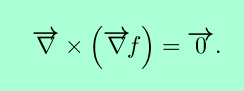World Web Math: Vector Calculus Summary

Vectors

(For much of these pages, vectors will be denoted by either a bold symbol, such as v for a generic vector or i for a unit vector when these quantities appear in the text. Overarrows may be used in displayed equations as well as the boldface symbols.)

If we adopt a cartesian coordinate system, then a three dimensional vector

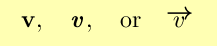
may be reprsented as the 3-tuple

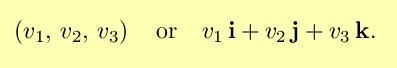
You can add vectors and multiply them by scalars:

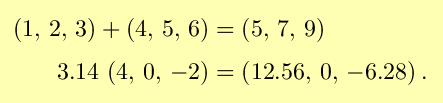
The magnitude of a vector v is denoted by

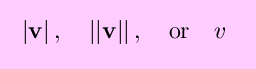
and is equal to

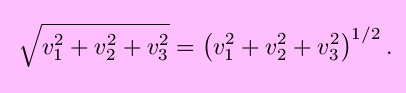
by the Pythagorean theorem, with similar forms for a higher or lower number of dimensions. A unit vector is a vector with magnitude 1, and any nonzero vector can be made into a unit vector by dividing by its magnitude.

There are two ways to multiply vectors: the dot product and the cross product. The two ways are quite different, and a major part of learning vector calculus is appreciating the difference. The dot product of two vectors v and w is the scalar value

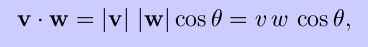
where the angle ``theta'' is the angle between v and w. Two nonzero vectors are orthogonal (perpendicular) if and only if their dot product is zero. It can be shown that

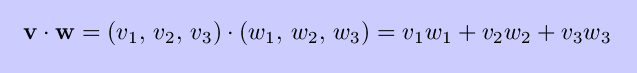
and that the projection of v onto w is

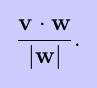
The cross product of two three-dimensional vectors is another vector, denoted

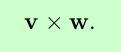
This vector has magnitude

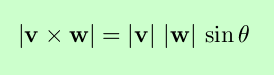
and direction orthogonal to the two vectors v and w, with orientation given by the right-hand rule. Two nonzero vectors are parallel if and only if their cross product is zero. Note that the magnitude of the cross product is also the area of the parallelogram with sides v and w. It can be shown that the cross product in 3-tuple form is

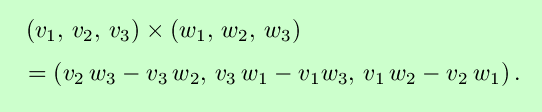
Vectors make it easier to describe our favorite geometric objects. For example, lines in three-space can be written parametrically as

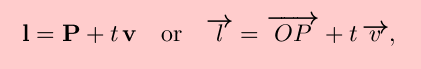
where P is a point on the line and v is a nonzero vector parallel to the line.

The plane with normal vector n that contains the point Q can be described implicitly by the equation

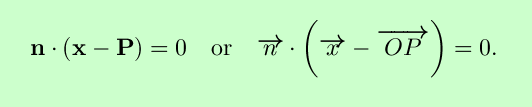
Cartesian coordinates are not the only way to label points in three-dimensional space. You might recall polar coordinates, which associated the pair of coordinates

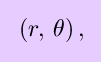
to each point in the plane, where the first coordinate is the distance from the origin and the second is the angle with respect to the positive x-axis. There are two different ways of generalizing polar coordinates to three dimensions: cylindrical and spherical coordinates. In cylindrical coordinates, each point has an r and a theta coordinate obtained by projecting the point onto the x-y plane and using the polar coordinates of the projection, plus a z coordinate which is the same as in cartesian coordinates. In spherical coordinates, every point is assigned three coordinates

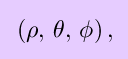
where the first (``rho'') is the distance from the origin, the second (``theta'', as in plane polar coordinates) is the angle that the vector from the origin to the point makes with the x-z plane, and the third (``phi'') is the angle that the vector makes with the positive z-axis.

Vector Calculus at A Glance

Function	Notation	Name	Derivatives	Integrals
		curve		path integral, line integral
		scalar field		double, triple, path and surface integrals
		parameterized surface		surface integral, flux integral
		vector field		line integral, flux integral

Scalar-valued functions

• Sections and level sets
• Graphing scalar valued functions
• Limits
• Continuity
• Directional derivatives
• Partial derivatives
• Total differentials
• The Derivative Matrix
• Tangent planes
• Linear approximation
• Differentiability
• The Simple Chain Rule
• The Matrix Chain Rule
• The Paths Chain Rule
• The gradient
• Iterated partial derivatives

Maximization and Minimization

1. Look at all the critical points x where the gradient of f(x) = 0. Throw out any that aren't in D.
2. Look at any points where f isn't differentiable.
3. Look at the boundary of D. You can this either by
   • Parameterizing the boundary so that you have an unconstrained max/min problem, or by
   • Lagrange multipliers: if the boundary of D is described as a level set by g(x) = 0, then the critical points of f constrained to be on the boundary of D can be found by solving
     

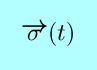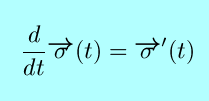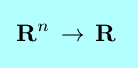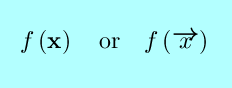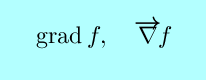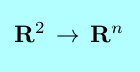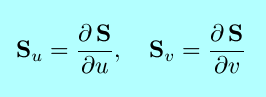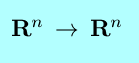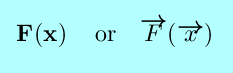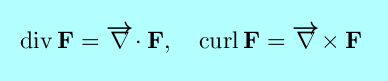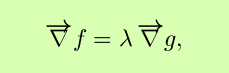
     the gradient of f is ``lamba'' times the gradient of g.

4. If x is the critical point in an unconstrained max/min problem, you can determine whether it is a local max, local min, or saddle point by looking at the Hessian.

Vector Fields

There are two derivatives which are useful in examining the local geometry of a vector field with n=2 or 3.

The divergence of F(x,y,z) is

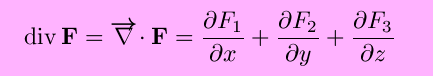
(only the first two terms if n=2) and measures the extent to which the point is a ``source'' or ``sink'' of the vector field.

The curl of F(x,y,z) is

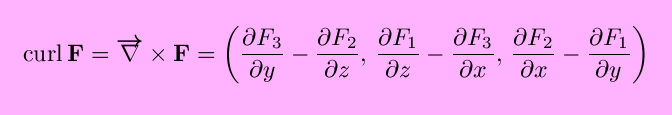
(only the z-component is nonzero if n=2) and measures the ``rotation'', or ``circulation per unit area'', of the vector field at a point.

Of special interest are gradient vector fields, those vector fields that are the gradient of some scalar potential function. Gradient vector fields are also called conservative vector fields, because the work done by a particle moving in a closed loop against a gradient vector field is always 0. The curl of a gradient vector field is the zero vector; this is useful in testing whether an arbitrary vector field is conservative. Symbolically,

Double and Triple Integrals

• Cavalieri's Principle
• Definition of Double Integral
• Fubini's Theorem
• Iterated Integrals
• Double Integrals over General Regions
• Changing the Order of Integration
• Triple Integrals
• Applications of Double and Triple Integrals
• Change of Variables

Surfaces

• Surface Area
• Scalar Surface Integrals
• Surface Flux Integrals

Fundamental Theorems of Vector Calculus

• FTC for Work Integrals
• Green's Theorem
• Stokes' Theorem
• Gauss' Theorem