Logical vs

Logical vs.Analogical

Symbolic vs. Connectionist

Neat vs. Scruffy

Marvin Minsky

In Artificial Intelligence at MIT, Expanding Frontiers, Patrick H. Winston (Ed.), Vol.1, MIT Press, 1990. Reprinted in AI Magazine, Summer 1991

<<INTRODUCTION BY PATRICK WINSTON>>

Engineering and scientific education conditions us to expect everything, including intelligence, to have a simple, compact explanation. Accordingly, when people new to AI ask "What's AI all about," they seem to expect an answer that defines AI in terms of a few basic mathematical laws.

Today, some researchers who seek a simple, compact explanation hope that systems modeled on neural nets or some other connectionist idea will quickly overtake more traditional systems based on symbol manipulation. Others believe that symbol manipulation, with a history that goes back millennia, remains the only viable approach.

Minsky subscribes to neither of these extremist views. Instead, he argues that Artificial Intelligence must employ many approaches. Artificial Intelligence is not like circuit theory and electromagnetism. AI has nothing so wonderfully unifying like Kirchhoff's laws are to circuit theory or Maxwell's equations are to electromagnetism. Instead of looking for a "Right Way," Minsky believes that the time has come to build systems out of diverse components, some connectionist and some symbolic, each with its own diverse justification.

Minsky, whose seminal contributions in Artificial Intelligence are established worldwide, is one of the 1990 recipients of the prestigious Japan Prize---a prize recognizing original and outstanding achievements in science and technology.

=================

Why is there so much excitement about Neural Networks today, and how is this related to research on Artificial Intelligence? Much has been said, in the popular press, as though these were conflicting activities. This seems exceedingly strange to me, because both are parts of the very same enterprise. What caused this misconception?

The symbol-oriented community in AI has brought this rift upon itself, by supporting models in research that are far too rigid and specialized. This focus on well-defined problems produced many successful applications, no matter that the underlying systems were too inflexible to function well outside the domains for which they were designed. (It seems to me that this happened because of the researchers' excessive concern with logical consistency and provability. Ultimately, that would be a proper concern, but not in the subject's present state of immaturity.) Thus, contemporary symbolic AI systems are now too constrained to be able to deal with exceptions to rules, or to exploit fuzzy, approximate, or heuristic fragments of knowledge. Partly in reaction to this, the connectionist movement initially tried to develop more flexible systems, but soon came to be imprisoned in its own peculiar ideology---of trying to build learning systems endowed with as little architectural structure as possible, hoping to create machines that could serve all masters equally well. The trouble with this is that even a seemingly neutral architecture still embodies an implicit assumption about which things are presumed to be "similar."

The field called Artificial Intelligence includes many different aspirations. Some researchers simply want machines to do the various sorts of things that people call intelligent. Others hope to understand what enables people to do such things. Yet other researchers want to simplify programming; why can't we build, once and for all, machines that grow and improve themselves by learning from experience? Why can't we simply explain what we want, and then let our machines do experiments, or read some books, or go to school---the sorts of things that people do. Our machines today do no such things: Connectionist networks learn a bit, but show few signs of becoming "smart;" symbolic systems are shrewd from the start, but don’t yet show any "common sense." How strange that our most advanced systems can compete with human specialists, yet be unable to do many things that seem easy to children. I suggest that this stems from the nature of what we call 'specialties'---for the very act of naming a specialty amounts to celebrating the discovery of some model of some aspect of reality, which is useful despite being isolated from most of our other concerns. These models have rules which reliably work---so long as we stay in that special domain. But when we return to the commonsense world, we rarely find rules that precisely apply. Instead, we must know how to adapt each fragment of `knowledge' to particular contexts and circumstances, and we must expect to need more and different kinds of knowledge as our concerns broaden. Inside such simple "toy" domains, a rule may seem to be quite "general," but whenever we broaden those domains, we find more and more exceptions---and the early advantage of context-free rules then mutates into strong limitations.

AI research must now move from its traditional focus on particular schemes. There is no one best way to represent knowledge, or to solve problems, and limitations of present-day machine intelligence stem largely from seeking "unified theories," or trying to repair the deficiencies of theoretically neat, but conceptually impoverished ideological positions. Our purely numerical connectionist networks are inherently deficient in abilities to reason well; our purely symbolic logical systems are inherently deficient in abilities to represent the all-important "heuristic connections” between things---the uncertain, approximate, and analogical linkages that we need for making new hypotheses. The versatility that we need can be found only in larger-scale architectures that can exploit and manage the advantages of several types of representations at the same time. Then, each can be used to overcome the deficiencies of the others. To do this, each formally neat type of knowledge representation or inference must be complemented with some "scruffier" kind of machinery that can embody the heuristic connections between the knowledge itself and what we hope to do with it.

Figure 1: Symbolic vs. Analogical Man: Top-Down vs. Bottom Up

While different workers have diverse goals, all AI researchers seek to make machines that solve problems. One popular way to pursue that quest is to start with a "top-down" strategy: begin at the level of commonsense psychology and try to imagine processes that could play a certain game, solve a certain kind of puzzle, or recognize a certain kind of object. If you can't do this in a single step, then keep breaking things down into simpler parts until you can actually embody them in hardware or software.

This basically reductionist technique is typical of the approach to AI called heuristic programming. These techniques have developed productively for several decades and, today, heuristic programs based on top-down analysis have found many successful applications in technical, specialized areas. This progress is largely due to the maturation of many techniques for representing knowledge. But the same techniques have seen less success when applied to "commonsense" problem solving. Why can we build robots that compete with highly trained workers to assemble intricate machinery in factories---but not robots that can help with ordinary housework? It is because the conditions in factories are constrained, while the objects and activities of everyday life are too endlessly varied to be described by precise, logical definitions and deductions. Commonsense reality is too disorderly to represent in terms of universally valid "axioms." To deal with such variety and novelty, we need more flexible styles of thought, such as those we see in human commonsense reasoning, which is based more on analogies and approximations than on precise formal procedures. Nonetheless, top-down procedures have important advantages in being able to perform efficient, systematic search procedures, to manipulate and rearrange the elements of complex situations, and to supervise the management of intricately interacting subgoals---all functions that seem beyond the capabilities of connectionist systems with weak architectures.

Short-sighted critics have always complained that progress in top-down symbolic AI research is slowing down. In one way this is natural: in the early phases of any field, it becomes ever harder to make important new advances as we put the easier problems behind us---and new workers must face a "squared" challenge, because there is so much more to learn. But the slowdown of progress in symbolic AI is not just a matter of laziness. Those top-down systems are inherently poor at solving problems which involve large numbers of weaker kinds of interactions, such as occur in many areas of pattern recognition and knowledge retrieval. Hence, there has been a mounting clamor for finding another, new, more flexible approach---and this is one reason for the recent popular turn toward connectionist models.

The bottom-up approach goes the opposite way. We begin with simpler elements---they might be small computer programs, elementary logical principles, or simplified models of what brain cells do---and then move upwards in complexity by finding ways to interconnect those units to produce larger scale phenomena. The currently popular form of this, the connectionist neural network approach, developed more sporadically than did heuristic programming. In part, this was because heuristic programming developed so rapidly in the 1960s that connectionist networks were swiftly outclassed. Also, the networks need computation and memory resources that were too prodigious for that period. Now that faster computers are available, bottom-up connectionist research has shown considerable promise in mimicking some of what we admire in the behavior of lower animals, particularly in the areas of pattern recognition, automatic optimization, clustering, and knowledge retrieval. But their performance has been far weaker in the very areas in which symbolic systems have successfully mimicked much of what we admire in high-level human thinking---for example, in goal-based reasoning, parsing, and causal analysis. These weakly structured connectionist networks cannot deal with the sorts of tree-search explorations, and complex, composite knowledge structures required for parsing, recursion, complex scene analysis, or other sorts of problems that involve "functional parallelism." It is an amusing paradox that connectionists frequently boast about the massive parallelism of their computations, yet the homogeneity and interconnectedness of those structures make them virtually unable to do more than one thing at a time- --at least, at levels above that of their basic associative functionality. This is essentially because they lack the architecture needed to maintain adequate short-term memories.

Thus, the present-day systems of both types show serious limitations. The top-down systems are handicapped by inflexible mechanisms for retrieving knowledge and reasoning about it, while the bottom-up systems are crippled by inflexible architectures and organizational schemes. Neither type of system has been developed so as to be able to exploit multiple, diverse varieties of knowledge.

Which approach is best to pursue? That is simply a wrong question. Each has virtues and deficiencies, and we need integrated systems that can exploit the advantages of both. In favor of the top-down side, research in Artificial Intelligence has told us a little---but only a little---about how to solve problems by using methods that resemble reasoning. If we understood more about this, perhaps we could more easily work down toward finding out how brain cells do such things. In favor of the bottom-up approach, the brain sciences have told us something---but again, only a little---about the workings of brain cells and their connections. More research on this might help us discover how the activities of brain-cell networks support our higher-level processes. But right now we're caught in the middle; neither purely connectionist nor purely symbolic systems seem able to support the sorts of intellectual performances we take for granted even in young children. This essay aims at understanding why both types of AI systems have developed to become so inflexible. I'll argue that the solution lies somewhere between these two extremes, and our problem will be to find out how to build a suitable bridge. We already have plenty of ideas at either extreme. On the connectionist side we can extend our efforts to design neural networks that can learn various ways to represent knowledge. On the symbolic side, we can extend our research on knowledge representations, and on designing systems that can effectively exploit the knowledge thus represented. But above all, at the present time, we need more research on how to combine both types of ideas.

REPRESENTATION AND RETRIEVAL: STRUCTURE AND FUNCTION

In order for a machine to learn, it must represent what it will learn. The knowledge must be embodied in some form of mechanism, data-structure, or other representation. Researchers in Artificial Intelligence have devised many ways to do this, for example, in the forms of:

Rule-based systems.
Frames with Default Assignments.
Predicate Calculus.
Procedural Representations.
Associative data bases.
Procedural representations.
Semantic Networks.
Object Oriented Programming.
Conceptual Dependency.
Action Scripts.
Neural Networks.
Natural Language.

In the 1960s and 1970s, students frequently asked, "Which kind of representation is best," and I usually replied that we'd need more research before answering that. But now I would give a different reply: "To solve really hard problems, we'll have to use several different representations." This is because each particular kind of data-structure has its own virtues and deficiencies, and none by itself seems adequate for all the different functions involved with what we call "common sense." Each has domains of competence and efficiency, so that one may work where another fails. Furthermore, if we rely only on any single "unified" scheme, then we'll have no way to recover from failure. As suggested in section 6.9 of The Society of Mind, (henceforth called "SOM"),

"The secret of what something means lies in how it connects to other things we know. That's why it's almost always wrong to seek the "real meaning" of anything. A thing with just one meaning has scarcely any meaning at all."

In order to get around these constraints, we must develop systems that combine the expressiveness and procedural versatility of symbolic systems with the fuzziness and adaptiveness of connectionist representations. Why has there been so little work on synthesizing these techniques? I suspect that it is because both of these AI communities suffer from a common cultural- philosophical disposition: they would like to explain intelligence in the image of what was successful in Physics---by minimizing the amount and variety of its assumptions. But this seems to be a wrong ideal; instead, we should take our cue from biology rather than from physics. This is because what we call "thinking" does not emerge directly from a few fundamental principles of wave-function symmetry and exclusion rules. Mental activities are not the sorts of unitary or "elementary" phenomenon that can be described by a few mathematical operations on logical axioms. Instead, the functions performed by the brain are the products of the work of thousands of different, specialized sub-systems, the intricate product of hundreds of millions of years of biological evolution. We cannot hope to understand such an organization by emulating the techniques of those particle physicists who search for the simplest possible unifying conceptions. Constructing a mind is simply a different kind of problem---of how to synthesize organizational systems that can support a large enough diversity of different schemes, yet enable them to work together to exploit one another's abilities.

To solve typical real-world commonsense problems, a mind must have at least several different kinds of knowledge. First, we need to represent goals: what is the problem to be solved. Then the system must also possess adequate knowledge about the domain or context in which that problem occurs. Finally, the system must know what kinds of reasoning are applicable in that area. Superimposed on all of this, our systems must have management schemes that can operate different representations and procedures in parallel, so that when any particular method breaks down or gets stuck, the system can quickly shift over to analogous operations in other realms that may be able to continue the work. For example, when you hear a natural language expression like,

"Mary gave Jack the book"

this will produce in you, albeit unconsciously, many different kinds of thoughts (see SOM 29.2)---that is, mental activities in such different realms as:

A visual representation of the scene.
Postural and Tactile representations of the experience.
A script-sequence of a typical script-sequence for "giving."
Representation of the participants' roles.
Representations of their social motivations.
Default assumptions about Jack, Mary and the book.
Other assumptions about past and future expectations.

How could a brain possibly coordinate the use of such different kinds of processes and representations? Our conjecture is that our brains construct and maintain them in different brain-agencies. (The corresponding neural structures need not, of course, be entirely separate in their spatial extents inside the brain.) But it is not enough to maintain separate processes inside separate agencies; we also need additional mechanisms to enable each of them to support the activities of the others---or, at least, to provide alternative operations in case of failures. Chapters 19 through 23 of SOM sketch some ideas about how the representations in different agencies could be coordinated. These sections introduce the concepts of:

Polyneme---a hypothetical neuronal mechanism for activating corresponding slots in different representations.

Microneme---a context-representing mechanism which similarly biases all the agencies to activate knowledge related to the current situation and goal.

Paranome---yet another mechanism that can apply corresponding processes or operations simultaneously to the short-term memory agents--- called pronomes---of those various agencies.

It is impossible to summarize briefly how all these mechanisms are imagined to work, but section 29.3 of SOM gives some of the flavor of our theory. What controls those paranomes? I suspect that, in human minds, this control comes from mutual exploitation between:

A long-range planning agency (whose scripts are influenced by various strong goals and ideals; this agency resembles the Freudian superego, and is based on early imprinting).

Another supervisory agency capable of using semi-formal inferences and natural-language reformulations.

A Freudian-like censorship agency that incorporates massive records of previous failures of various sorts.

RELEVANCE AND SIMILARITY

Problem-solvers must find relevant data. How does the human mind retrieve what it needs from among so many millions of knowledge items? Different AI systems have attempted to use a variety of different methods for this. Some assign keywords, attributes, or descriptors to each item and then locate data by feature-matching or by using more sophisticated associative data-base methods. Others use graph-matching or analogical case-based adaptation. Yet others try to find relevant information by threading their ways through systematic, usually hierarchical classifications of knowledge---sometimes called "ontologies". But, to me, all such ideas seem deficient because it is not enough to classify items of information simply in terms of the features or structures of those items themselves. This is because we rarely use a representation in an intentional vacuum, but we always have goals---and two objects may seem similar for one purpose but different for another purpose. Consequently, we must also take into account the functional aspects of what we know, and therefore we must classify things (and ideas) according to what they can be used for, or which goals they can help us achieve. Two armchairs of identical shape may seem equally comfortable as objects for sitting in, but those same chairs may seem very different for other purposes, for example, if they differ much in weight, fragility, cost, or appearance. The further a feature or difference lies from the surface of the chosen representation, the harder it will be to respond to, exploit, or adapt to it---and this is why the choice of representation is so important. In each functional context we need to represent particularly well the heuristic connections between each object's internal features and relationships, and the possible functions of those objects. That is, we must be able to easily relate the structural features of each object's representation to how that object might behave in regard to achieving our present goals. This is further discussed in sections 12.4, 12.5, 12.12, and 12.13 of SOM.

Figures 2A and 2B: ARM-CHAIR

New problems, by definition, are different from those we have already encountered; so we cannot always depend on using records of past experience--and yet, to do better than random search, we have to exploit what was learned from the past, no matter that it may not perfectly match. Which records should we retrieve as likely to be the most relevant?

Explanations of "relevance," in traditional theories, abound with synonyms for nearness and similarity. If a certain item gives bad results, it makes sense to try something different. But when something we try turns out to be good, then a similar one may be better. We see this idea in myriad forms, and whenever we solve problems we find ourselves employing metrical metaphors: we're "getting close" or "on the right track;" using words that express proximity. But what do we mean by "close" or "near." Decades of research on different forms of that question have produced theories and procedures for use in signal processing, pattern recognition, induction, classification, clustering, generalization, etc., and each of these methods has been found useful for certain applications, but ineffective for others. Recent connectionist research has considerably enlarged our resources in these areas. Each method has its advocates---but I contend that it is now time to move to another stage of research. For, although each such concept or method may have merit in certain domains, none of them seem powerful enough alone to make our machines more intelligent. It is time to stop arguing over which type of pattern classification technique is best--- because that depends on our context and goal. Instead, we should work at a higher level of organization, to discover how to build managerial systems to exploit the different virtues, and to evade the different limitations, of each of these ways of comparing things. Different types of problems, and representations, may require different concepts of similarity. Within each realm of discourse, some representation will make certain problems and concepts appear to be more closely related than others. To make matters worse, even within the same problem domain, we may need different notions of similarity for:

Descriptions of problems and goals.
Descriptions of knowledge about the subject domain.
Descriptions of procedures to be used.

For small domains, we can try to apply all of our reasoning methods to all of our knowledge, and test for satisfactory solutions. But this is usually impractical, because the search becomes too huge---in both symbolic and connectionist systems. To constrain the extent of mindless search, we must incorporate additional kinds of knowledge---embodying expertise about problem-solving itself and, particularly, about managing the resources that may be available. The spatial metaphor helps us think about such issues by providing us with a superficial unification: if we envision problem-solving as "searching for solutions" in a space-like realm, then it is tempting to analogize between the ideas of similarity and nearness: to think about similar things as being in some sense near or close to one another.

Figure 3: FOOT-WHEEL: functional similarity

But "near" in what sense? To a mathematician, the most obvious idea would be to imagine the objects under comparison to be like points in some abstract space; then each representation of that space would induce (or reflect) some sort of topology-like structure or relationship among the possible objects being represented. Thus, the languages of many sciences, not merely those of Artificial Intelligence and of psychology, are replete with attempts to portray families of concepts in terms of various sorts of spaces equipped with various measures of similarity. If, for example, you represent things in terms of (allegedly independent) properties then it seems natural to try to assign magnitudes to each, and then to sum the squares of their differences---in effect, representing those objects as vectors in Euclidean space. This further encourages us to formulate the function of knowledge in terms of helping us to decide "which way to go." This is often usefully translated into the popular metaphor of "hill-climbing" because, if we can impose on that space a suitable metrical structure, we may be able to devise iterative ways to find solutions by analogy with the method of hill- climbing or gradient ascent---that is, when any experiment seems more or less successful than another, then we exploit that metrical structure to help us make the next move in the proper "direction." (Later, we shall emphasize that having a sense of direction entails a little more than a sense of proximity; it is not enough just to know metrical distances, we must also respond to other kinds of heuristic differences---and these may be difficult to detect.)

Figure. 4: HILL-CLIMBING - "Heureka!"

Whenever we design or select a particular representation, that particular choice will bias our dispositions about which objects to consider more or less similar to us (or, to the programs we apply to them) and thus will affect how we apply our knowledge to achieve goals and solve problems. Once we understand the effects of such commitments, we will be better prepared to select and modify those representations to produce more heuristically useful distinctions and confusions. So, let us now examine, from this point of view, some of the representations that have become popular in the field of Artificial Intelligence.

HEURISTIC CONNECTIONS OF PURE LOGIC

Why have logic-based formalisms been so widely used in AI research? I see two motives for selecting this type of representation. One virtue of logic is clarity, its lack of ambiguity. Another advantage is the pre-existence of many technical mathematical theories about logic. But logic also has its disadvantages. Logical generalizations apply only to their literal lexical instances, and logical implications apply only to expressions that precisely instantiate their antecedent conditions. No exceptions at all are allowed, no matter how "closely" they match. This permits you to use no near misses, no suggestive clues, no compromises, no analogies, and no metaphors. To shackle yourself so inflexibly is to shoot your own mind in the foot---if you know what I mean.

These limitations of logic begin at the very foundation, with the basic connectives and quantifiers. The trouble is that worldly statements of the form, "For all $X$, $P(X)$," are never beyond suspicion. To be sure, such a statement can indeed be universally valid inside a mathematical realm--- but this is because such realms, themselves, are based on expressions of those very kinds. The use of such formalisms in AI have led most researchers to seek "truth" and universal "validity" to the virtual exclusion of "practical" or "interesting"---as though nothing would do except certainty. Now, that is acceptable in mathematics (wherein we ourselves define the worlds in which we solve problems) but, when it comes to reality, there is little advantage in demanding inferential perfection, when there is no guarantee even that our assumptions will always be correct. Logic theorists seem to have forgotten that in actual life, any expression like "For all X$, P(X)"--that is, in any world which we find, but don't make---must be seen as only a convenient abbreviation for something more like this:

"For any thing X being considered in the current context, the assertion P(X) is likely to be useful for achieving goals like G, provided that we apply in conjunction with certain heuristically appropriate inference methods."

In other words, we cannot ask our problem-solving systems to be absolutely perfect, or even consistent; we can only hope that they will grow increasingly better than blind search at generating, justifying, supporting, rejecting, modifying, and developing "evidence" for new hypotheses.

Figure 5: EGG - Default Assumption

It has become particularly popular, in AI logic programming, to restrict the representation to expressions written in the first order predicate calculus. This practice, which is so pervasive that most students engaged in it don't even know what "first order" means here, facilitates the use of certain types of inference, but at a very high price: that the predicates of such expressions are prohibited from referring in certain ways to one another. This prevents the representation of meta-knowledge, rendering those systems incapable, for example, of describing what the knowledge that they contain can be used for. In effect, it precludes the use of functional descriptions. We need to develop systems for logic that can reason about their own knowledge, and make heuristic adaptations and interpretations of it, by using knowledge about that knowledge---but these limitations of expressiveness make logic unsuitable for such purposes.

Furthermore, it must be obvious that in order to apply our knowledge to commonsense problems, we need to be able to recognize which expressions are similar, in whatever heuristic sense may be appropriate. But this, too, seems technically impractical, at least for the most commonly used logical formalisms---namely, expressions in which absolute quantifiers range over string-like normal forms. For example, in order to use the popular method of "resolution theorem-proving," one usually ends up using expressions that consist of logical disjunctions of separately almost meaningless conjunctions. Consequently, the "natural topology" of any such representation will almost surely be heuristically irrelevant to any real-life problem space. Consider how dissimilar these three expressions seem, when written in conjunctive form:

AvBvCvD ABvACvADvBCvBDvCD ABCvABDvACDvBCD

The simplest way to assess the distances or differences between expressions is to compare such superficial factors as the numbers of terms or sub-expressions they have in common. Any such assessment would seem meaningless for expressions like those above. In most situations, however, it would almost surely be more useful to recognize that these expressions are symmetric in their arguments, and hence will clearly seem more similar if we re-represent them, for example, by using S(n) to mean "n of S's arguments have truth-value T." Then those same expressions can be written in the simpler forms S(1), S(2), S(3),

Even in mathematics itself, we consider it a great discovery to find a new representation for which the most natural- seeming heuristic connection can be recognized as close to the representation's surface structure. But this is too much to expect in general, so it is usually necessary to gauge the similarity of two expressions by using more complex assessments based, for example, on the number of set- inclusion levels between them, or on the number of available operations required to transform one into the other, or on the basis of the partial ordering suggested by their lattice of common generalizations and instances. This means that making good similarity judgments may itself require the use of other heuristic kinds of knowledge, until eventually---that is, when our problems grow hard enough---we are forced to resort to techniques that exploit knowledge that is not so transparently expressed in any such "mathematically elegant" formulation.

Indeed, we can think about much of Artificial Intelligence research in terms of a tension between solving problems by searching for solutions inside a compact and well-defined problem space (which is feasible only for prototypes)---versus using external systems (that exploit larger amounts of heuristic knowledge) to reduce the complexity of that inner search. Compound systems of that sort need retrieval machinery that can select and extract knowledge which is "relevant" to the problem at hand. Although it is not especially hard to write such programs, it cannot be done in "first order" systems. In my view, this can best be achieved in systems that allow us to use, simultaneously, both object-oriented structure-based descriptions and goal-oriented functional descriptions.

How can we make Formal Logic more expressive, given that each fundamental quantifier and connective is defined so narrowly from the start? This could well be beyond repair, and the most satisfactory replacement might be some sort of object-oriented frame-based language. After all, once we leave the domain of abstract mathematics, and free ourselves from those rigid notations, we can see that some virtues of logic-like reasoning may still remain---for example, in the sorts of deductive chaining we used, and the kinds of substitution procedures we applied to those expressions. The spirit of some of these formal techniques can then be approximated by other, less formal techniques of making chains, like those suggested in chapter 18 of SOM. For example, the mechanisms of defaults and frame-arrays could be used to approximate the formal effects of instantiating generalizations. When we use heuristic chaining, of course, we cannot assume absolute validity of the result, and so, after each reasoning step, we may have to look for more evidence. If we notice exceptions and disparities then, later, we must return again to each, or else remember them as assumptions or problems to be justified or settled at some later time---all things that humans so often do.

HEURISTIC CONNECTIONS OF RULE-BASED SYSTEMS

While logical representations have been used in popular research, rule- based representations have been more successful in applications. In these systems, each fragment of knowledge is represented by an IF-THEN rule so that, whenever a description of the current problem-situation precisely matches the rule's antecedent IF condition, the system performs the action described by that rule's THEN consequent. What if no antecedent condition applies? Simple: the programmer adds another rule. It is this seeming modularity that made rule-based systems so attractive. You don't have to write complicated programs. Instead, whenever the system fails to perform, or does something wrong, you simply add another rule. This usually works quite well at first---but whenever we try to move beyond the realm of "toy" problems, and start to accumulate more and more rules, we usually get into trouble because each added rule is increasingly likely to interact in unexpected ways with the others. Then what should we ask the program to do, when no antecedent fits perfectly? We can equip the program to select the rule whose antecedent most closely describes the situation---and, again, we're back to "similar." To make any real-world application program resourceful, we must supplement its formal reasoning facilities with matching facilities that are heuristically appropriate for the problem domain it is working in.

What if several rules match equally well? Of course, we could choose the first on the list, or choose one at random, or use some other superficial scheme---but why be so unimaginative? In SOM, we try to regard conflicts as opportunities rather than obstacles---an opening that we can use to exploit other kinds of knowledge. For example, section 3.2 of SOM suggests invoking a "Principle of Non-Compromise", to discard sets of rules with conflicting antecedents or consequents. The general idea is that whenever two fragments of knowledge disagree, it may be better to ignore them both, and refer to some other, independent agency. In effect this is a managerial approach in which one agency can engage some other body of expertise to help decide which rules to apply. For example, one might turn to case-based reasoning, to ask which method worked best in similar previous situations.

Yet another approach would be to engage a mechanism for inventing a new rule, by trying to combine elements of those rules that almost fit already. Section 8.2 of SOM suggests using K-line representations for this purpose. To do this, we must be immersed in a society-of-agents framework in which each response to a situation involves activating not one, but a variety of interacting processes. In such a system, all the agents activated by several rules can then be left to interact, if only momentarily, both with one another and with the input signals, so as to make a useful self-selection about which of them should remain active. This could be done by combining certain present-day connectionist concepts with other ideas about K-line mechanisms. But we cannot do this until we learn how to design network architectures that can support new forms of internal management and external supervision of developmental staging.

In any case, present-day rule-based systems are still are too limited in ability to express "typical" knowledge. They need better default machinery. They deal with exceptions too passively; they need censors. They need better "ring-closing" mechanisms for retrieving knowledge (see 19.10 of SOM). Above all, we need better ways to connect them with other kinds of representations, so that we can use them in problem-solving organizations that can exploit other kinds of models and search procedures.

CONNECTIONIST NETWORKS

Up to this point, we have considered ways to overcome the deficiencies of symbolic systems by augmenting them with connectionist machinery. But this kind of research should go both ways. Connectionist systems have equally crippling limitations, which might be ameliorated by augmentation with the sorts of architectures developed for symbolic applications. Perhaps such extensions and synthesis will recapitulate some aspects of how the primate brain grew over millions of years, by evolving symbolic systems to supervise its primitive connectionist learning mechanisms.

Figure 6: Weighty Decisions

What do we mean by "connectionist"? The usage of that term is still evolving rapidly, but here it refers to attempts to embody knowledge by assigning numerical conductivities or weights to the connections inside a network of nodes. The most common form of such a node is made by combing an analog, nearly linear part that "adds up evidence" with a nonlinear, nearly digital part that "makes a decision" based on a threshold. The most popular such networks today, take the form of multilayer perceptrons---that is, of sequences of layers of such nodes, each sending signals to the next. More complex arrangements are also under study; these can support cyclic internal activities, hence they are potentially more versatile, but harder to understand. What makes such architectures attractive? Mainly, that they appear to be so simple and homogeneous. At least on the surface, they can be seen as ways to represent knowledge without any complex syntax. The entire configuration-state of such a net can be described as nothing more than a simple vector---and the network's input-output characteristics as nothing more than a map from one vector space into another. This makes it easy to reformulate pattern-recognition and learning problems in simple terms---for example, finding the "best" such mapping, etc. Seen in this way, the subject presents a pleasing mathematical simplicity. It is often not mentioned that we still possess little theoretical understanding of the computational complexity of finding such mappings---that is, of how to discover good values for the connection- weights. Most current publications still merely exhibit successful small-scale examples without probing either into assessing the computational difficulty of those problems themselves, or of scaling those results to similar problems of larger size.

However, we now know of quite a few situations in which even such simple systems have been made to compute (and, more important, to learn to compute) interesting functions, particularly in such domains as clustering, classification, and pattern recognition. In some instances, this has occurred without any external supervision; furthermore, some of these systems have also performed acceptably in the presence of incomplete or noisy inputs---and thus correctly recognized patterns that were novel or incomplete. This means that the architectures of those systems must indeed have embodied heuristic connectivities that were appropriate for those particular problem-domains. In such situations, these networks can be useful for the kind of reconstruction-retrieval operations we call "Ring-Closing."

But connectionist networks have limitations as well. The next few sections discuss some of these limitations, along with suggestions on how to overcome them by embedding these networks in more advanced architectural schemes.

FRAGMENTATION, AND "THE PARALLEL PARADOX"

In our Epilogue to [Perceptrons], Papert and I argued as follows:

"It is often argued that the use of distributed representations enables a system to exploit the advantages of parallel processing. But what are the advantages of parallel processing? Suppose that a certain task involves two unrelated parts. To deal with both concurrently, we would have to maintain their representations in two decoupled agencies, both active at the same time. Then, should either of those agencies become involved with two or more sub-tasks, we'd have to deal with each of them with no more than a quarter of the available resources! If that proceeded on and on, the system would become so fragmented that each job would end up with virtually no resources assigned to it. In this regard, distribution may oppose parallelism: the more distributed a system is---that is, the more intimately its parts interact---the fewer different things it can do at the same time. On the other side, the more we do separately in parallel, the less machinery can be assigned to each element of what we do, and that ultimately leads to increasing fragmentation and incompetence. This is not to say that distributed representations and parallel processing are always incompatible. When we simultaneously activate two distributed representations in the same network, they will be forced to interact. In favorable circumstances, those interactions can lead to useful parallel computations, such as the satisfaction of simultaneous constraints. But that will not happen in general; it will occur only when the representations happen to mesh in suitably fortunate ways. Such problems will be especially serious when we try to train distributed systems to deal with problems that require any sort of structural analysis in which the system must represent relationships between substructures of related types---that is, problems that are likely to demand the same structural resources." (See also section 15.11 of SOM.)

For these reasons, it will always be hard for a homogeneous network to perform parallel "high-level" computations---unless we can arrange for it to become divided into effectively disconnected parts. There is no general remedy for this---and the problem is no special peculiarity of connectionist hardware; computers have similar limitations, and the only answer is providing more hardware. More generally, it seems obvious that without adequate memory buffering, homogeneous networks must remain incapable of recursion, so long as successive "function calls" have to use the same hardware. This is because, without such facilities, either the different calls will side-effect one another, or some of them must be erased, leaving the system unable to execute proper returns or continuations. Again, this may be easily fixed by providing enough short-term memory, for example, in the form of a stack of temporary K-lines.

LIMITATIONS OF SPECIALIZATION AND EFFICIENCY

Each connectionist net, once trained, can do only what it has learned to do. To make it do something else---for example, to compute a different measure of similarity, or to recognize a different class of patterns---would, in general, require a complete change in the matrix of connection coefficients. Usually, we can change the functionality of a computer much more easily (at least, when the desired functions can each be computed by compact algorithms); this is because a computer's "memory cells" are so much more interchangeable. It is curious how even technically well-informed people tend to forget how computationally massive a fully connected neural network is. It is instructive to compare this with the few hundred rules that drive a typically successful commercial rule-based Expert System.

How connected need networks be? There are several points in SOM that suggest that commonsense reasoning systems may not need to increase in the density of physical connectivity as fast as they increase the complexity and scope of their performances. Chapter 6 argues that knowledge systems must evolve into clumps of specialized agencies, rather than homogeneous networks, because they develop different types of internal representations. When this happens, it will become neither feasible nor practical for any of those agencies to communicate directly with the interior of others. Furthermore, there will be a tendency for newly acquired skills to develop from the relatively few that are already well developed and this, again, will bias the largest scale connections toward evolving into recursively clumped, rather than uniformly connected arrangements. A different tendency to limit connectivities is discussed in section 20.8, which proposes a sparse connection-scheme that can simulate, in real time, the behavior of fully connected nets---in which only a small proportion of agents are simultaneously active. This method, based on a half-century old idea of Calvin Mooers, allows many intermittently active agents to share the same relatively narrow, common connection bus. This might seem, at first, a mere economy, but section 20.9 suggests that this technique could also induce a more heuristically useful tendency, if the separate signals on that bus were to represent meaningful symbols. Finally, chapter 17 suggests other developmental reasons why minds may be virtually forced to grow in relatively discrete stages rather than as homogeneous networks. Our progress in this area may parallel our progress in understanding the stages we see in the growth of every child's thought.

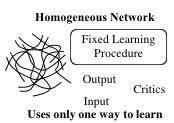
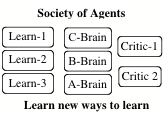
Figure. 7: Messy vs. Neat: Homostructural vs. Heterostructural

If our minds are assembled of agencies with so little inter-communication, how can those parts cooperate? What keeps them working on related aspects of the same problem? The first answer proposed in SOM is that it is less important for agencies to co-operate than to exploit one another. This is because those agencies tend to become specialized, developing their own internal languages and representations. Consequently, they cannot understand each other's internal operations very well---and each must learn to learn to exploit some of the others for the effects that those others produce---without knowing in any detail how those other effects are produced. For the same kind of reason, there must be other agencies to manage all those specialists, to keep the system from too much fruitless conflict for access to limited resources. Those management agencies themselves cannot deal directly with all the small interior details of what happens inside their subordinates. They must work, instead, with summaries of what those subordinates seem to do. This too, suggests that there must be constraints on internal connectivity: too much detailed information would overwhelm those managers. And this applies recursively to the insides of every large agency. So we argue, in chapter~8 of SOM, that relatively few direct connections are needed except between adjacent "level bands."

All this suggests (but does not prove) that large commonsense reasoning systems will not need to be "fully connected." Instead, the system could consist of localized clumps of expertise. At the lowest levels these would have to be very densely connected, in order to support the sorts of associativity required to learn low-level pattern detecting agents. But as we ascend to higher levels, the individual signals must become increasingly abstract and significant and, accordingly, the density of connection paths between agencies can become increasingly (but only relatively) smaller. Eventually, we should be able to build a sound technical theory about the connection densities required for commonsense thinking, but I don't think that we have the right foundations as yet. The problem is that contemporary theories of computational complexity are still based too much on worst-case analyses, or on coarse statistical assumptions---neither of which suitably represents realistic heuristic conditions. The worst-case theories unduly emphasize the intractable versions of problems which, in their usual forms, present less practical difficulty. The statistical theories tend to uniformly weight all instances, for lack of systematic ways to emphasize the types of situations of most practical interest. But the AI systems of the future, like their human counterparts, will normally prefer to satisfy rather than optimize---and we don't yet have theories that can realistically portray those mundane sorts of requirements.

LIMITATIONS OF CONTEXT, SEGMENTATION, AND PARSING

When we see seemingly successful demonstrations of machine learning, in carefully prepared test situations, we must be careful about how we draw more general conclusions. This is because there is a large step between the abilities to recognize objects or patterns (1) when they are isolated and (2) when they appear as components of more complex scenes. In section 6.6 of [Perceptrons] we see that we must be prepared to find that even after training a certain network to recognize a certain type of pattern, we may find it unable to recognize that same pattern when embedded in a more complicated context or environment. (Some reviewers have objected that our proofs of this applied only to simple three-layer networks; however, most of those theorems are quite general, as those critics might see, if they'd take the time to extend those proofs.) The problem is that it is usually easy to make isolated recognitions by detecting the presence of various features, and then computing weighted conjunctions of them. Clearly, this is easy to do, even in three-layer acyclic nets. But in compound scenes, this will not work unless the separate features of all the distinct objects are somehow properly assigned to those correct "objects." For the same kind of reason, we cannot expect neural networks to be generally able to parse the tree-like or embedded structures found in the phrase structure of natural language.

Figure. 8: Robot dog & Dinosaur - Recognition in Context

How could we augment connectionist networks to make them able to do such things as to analyze complex visual scenes, or to extract and assign the referents of linguistic expressions to the appropriate contents of short-term memories? This will surely need additional architecture to represent that structural analysis of, for example, a visual scene into objects and their relationships, by protecting each mid-level recognizer from seeing inputs derived from other objects, perhaps by arranging for the object-recognizing agents to compete to assign each feature to itself, while denying it to competitors. This has been done successfully in symbolic systems, and parts have been done in connectionist systems (for example, by Waltz and Pollack) but there remain many conceptual missing links in this area--- particularly in regard to how another connectionist system could use the output of one that managed to parse the scene. In any case, we should not expect to see simple solutions to these problems, for it may be no accident that such a large proportion of the primate brain is occupied with such functions.

LIMITATIONS OF OPACITY

Most serious of all is what we might call the Problem of Opacity: the knowledge embodied inside a network's numerical coefficients is not accessible outside that net. This is not a challenge we should expect our connectionists to easily solve. I suspect it is so intractable that even our own brains have evolved little such capacity over the billions of years it took to evolve from anemone-like reticulae. Instead, I suspect that our societies and hierarchies of sub-systems have evolved ways to evade the problem, by arranging for some of our systems to learn to "model" what some of our other systems do (see SOM, section 6.12). They may do this, partly, by using information obtained from direct channels into the interiors of those other networks, but mostly, I suspect, they do it less directly—so to speak, behavioristically—by making generalizations based on external observations, as though they were like miniature scientists. In effect, some of our agents invent models of others. Regardless of whether these models may be defective, or even entirely wrong (and here I refrain from directing my aim at peculiarly faulty philosophers), it suffices for those models to be useful in enough situations. To be sure, it might be feasible, in principle, for an external system to accurately model a connectionist network from outside, by formulating and testing hypotheses about its internal structure. But of what use would such a model be, if it merely repeated, redundantly? It would not only be simpler, but also more useful for that higher-level agency to assemble only a pragmatic, heuristic model of that other network's activity, based on concepts already available to that observer. (This is evidently the situation in human psychology. The apparent insights we gain from meditation and other forms of self- examination are genuine only infrequently.)

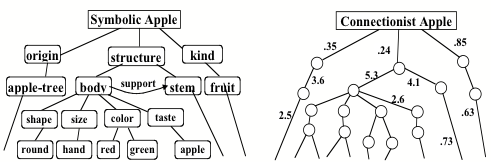
Figure. 9: Numerical Opacity: Symbolic Apple vs. Connectionist Apple

The problem of opacity grows more acute as representations become more distributed---that is, as we move from symbolic to connectionist poles---and it becomes increasingly more difficult for external systems to analyze and reason about the delocalized ingredients of the knowledge inside distributed representations. It also makes it harder to learn, past a certain degree of complexity, because it is hard to assign credit for success, or to formulate new hypotheses (because the old hypotheses themselves are not "formulated"). Thus, distributed learning ultimately limits growth, no matter how convenient it may be in the short term, because "the idea of a thing with no parts provides nothing that we can use as pieces of explanation" (see SOM, section 5.3).

For such reasons, while homogeneous, distributed learning systems may work well to a certain point, they should eventually start to fail when confronted with problems of larger scale---unless we find ways to compensate the accumulation of many weak connections with some opposing mechanism that favors toward internal simplification and localization. Many connectionist writers seem positively to rejoice in the holistic opacity of representations within which even they are unable to discern the significant parts and relationships. But unless a distributed system has enough ability to crystallize its knowledge into lucid representations of its new sub-concepts and substructures, its ability to learn will eventually slow down and it will be unable to solve problems beyond a certain degree of complexity. And although this suggests that homogeneous network architectures may not work well past a certain size, this should be bad news only for those ideologically committed to minimal architectures. For all we know at the present time, the scales at which such systems crash are quite large enough for our purposes. Indeed, the Society of Mind thesis holds that most of the "agents" that grow in our brains need operate only on scales so small that each by itself seems no more than a toy. But when we combine enough of them---in ways that are not too delocalized---we can make them do almost anything.

In any case, we should not assume that we always can---or always should--- avoid the use of opaque schemes. The circumstances of daily life compel us to make decisions based on "adding up the evidence." We frequently find (when we value our time) that, even if we had the means, it wouldn't pay to analyze. Nor does the Society of Mind theory of human thinking suggest otherwise; on the contrary it leads us to expect to encounter incomprehensible representations at every level of the mind. A typical agent does little more than exploit other agents' abilities---hence most of our agents accomplish their job knowing virtually nothing of how it is done.

Analogous issues of opacity arise in the symbolic domain. Just as networks sometimes solve problems by using massive combinations of elements each of which has little individual significance, symbolic systems sometimes solve problems by manipulating large expressions with similarly insignificant terms, as when we replace the explicit structure of a composite Boolean function by a locally senseless canonical form. Although this simplifies some computations by making them more homogeneous, it disperses knowledge about the structure and composition of the data---and thus disables our ability to solve harder problems. At both extremes---in representations that are either too distributed or too discrete---we lose the structural knowledge embodied in the form of intermediate-level concepts. That loss may not be evident, as long as our problems are easy to solve, but those intermediate concepts may be indispensable for solving more advanced problems. Comprehending complex situations usually hinges on discovering a good analogy or variation on a theme. But it is virtually impossible to do this with a representation, such as a logical form, a linear sum, or a holographic transformation---each of whose elements seem meaningless because they are either too large or too small---and thus leaving no way to represent significant parts and relationships.

There are many other problems that invite synthesizing symbolic and connectionist architectures. How can we find ways for nodes to "refer" to other nodes, or to represent knowledge about the roles of particular coefficients? To see the difficulty, imagine trying to represent the structure of the Arch in Patrick Winston's thesis---without simply reproducing that topology. Another critical issue is how to enable nets to make comparisons. This problem is more serious than it might seem. Section 23.1 of [SOM] discusses the importance of "Differences and Goals," and section 23.2 points out that connectionist networks deficient in memory will find it peculiarly difficult to detect differences between patterns. Networks with weak architectures will also find it difficult to detect or represent (invariant) abstractions; this problem was discussed as early as the Pitts- McCulloch paper of 1947. Yet another important problem for memory- weak, bottom-up mechanisms is that of controlling search: In order to solve hard problems, one may have to consider different alternatives, explore their sub-alternatives, and then make comparisons among them---yet still be able to return to the initial situation without forgetting what was accomplished. This kind of activity, which we call "thinking," requires facilities for temporarily storing partial states of the system without confusing those memories. One answer is to provide, along with the required memory, some systems for learning and executing control scripts, as suggested in section 13.5 of SOM. To do this effectively, we must have some "Insulationism" to counterbalance our "connectionism". Smart systems need both of those components, so the symbolic-connectionist antagonism is not a valid technical issue, but only a transient concern in contemporary scientific politics.

MIND-SCULPTURE

The future work of mind design will not be much like what we do today. Some programmers will continue to use traditional languages and processes. Others programmers will turn toward new kinds of knowledge-based expert systems. But eventually all of this will be incorporated into systems that exploit two new kinds of resources. On one side, we will use huge pre-programmed reservoirs of commonsense knowledge. On the other side, we will have powerful, modular learning machines equipped with no knowledge at all. Then what we know as programming will change its character entirely---to an activity that I envision as more like sculpturing. To program today, we must describe things very carefully, because nowhere is there any margin for error. But once we have modules that know how to learn, we won't have to specify nearly so much---and we'll program on a grander scale, relying on learning to fill in the details.

This doesn't mean, I hasten to add, that things will be simpler than they are now. Instead we'll make our projects more ambitious. Designing an artificial mind will be much like evolving an animal. Imagine yourself at a terminal, assembling various parts of a brain. You'll be specifying the sorts of things that we've only been described heretofore in texts about neuroanatomy. "Here," you'll find yourself thinking, "We'll need two similar networks that can learn to shift time-signals into spatial patterns so that they can be compared by a feature extractor sensitive to a context about this wide." Then you'll have to sketch the architectures of organs that can learn to supply appropriate inputs to those agencies, and draft the outlines of intermediate organs for learning to suitably encode the outputs to suit the needs of other agencies. Section 31.3 of SOM suggests how a genetic system might mold the form of an agency that is predestined to learn to recognize the presence of particular human individuals. A functional sketch of such a design might turn out to involve dozens of different sorts of organs, centers, layers, and pathways. The human brain might have many thousands of such components.

A functional sketch is only the start. Whenever you employ a learning machine, you must specify more than merely the sources of inputs and destinations of outputs. It must also, somehow, be impelled toward the sorts of things you want it to learn---what sorts of hypotheses it should make, how it should compare alternatives, how many examples should be required, and how to decide when enough has been done; when to decide that things have gone wrong, and how to deal with bugs and exceptions. It is all very well for theorists to speak about "spontaneous learning and generalization," but there are too many contingencies in real life for such words to mean anything by themselves. Should that agency be an adventurous risk-taker or a careful, conservative reductionist? One person's intelligence is another's stupidity. And how should that learning machine divide and budget its resources of hardware, time, and memory?

How will we build those grand machines, when so many design constraints are involved? No one will be able to keep track of all the details because, just as a human brain is constituted by interconnecting hundreds of different kinds of highly evolved sub-architectures, so will those new kinds of thinking machines. Each new design will have to be assembled by using libraries of already developed, off-the-shelf sub-systems already known to be able to handle particular kinds of representations and processing---and the designer will be less concerned with what happens inside these units, and more concerned with their interconnections and interrelationships. Because most components will be learning machines, the designer will have to specify, not only what each one will learn, but also which agencies should provide what incentives and rewards for which others. Every such decision about one agency imposes additional constraints and requirements on several others---and, in turn, on how to train those others. And, as in any society, there must be watchers to watch each watcher, lest any one or a few of them get too much control of the rest.

Each agency will need nerve-bundle-like connections to certain other ones, for sending and receiving signals about representations, goals, and constraints---and we'll have to make decisions about the relative size and influence of every such parameter. Consequently, I expect that the future art of brain design will have to be more like sculpturing than like our present craft of programming. It will be much less concerned with the algorithmic details of the sub-machines than with balancing their relationships; perhaps this better resembles politics, sociology, or management than present-day engineering.

Some neural-network advocates might hope that all this will be superfluous. Perhaps, they expect us to find simpler ways. Why not seek to find, instead, how to build one single, huge net that can learn to do all those things by itself. That could, in principle, be done since our own human brains themselves came about as the outcome of one great learning-search. We could regard this as proving that just such a project is feasible---but only by ignoring the facts---the unthinkable scale of that billion year venture, and the octillions of lives of our ancestors. Remember too that, even so, in all that evolutionary search, not all the problems have yet been solved. What will we do when our sculptures don't work? Consider a few of the wonderful bugs that still afflict even our own grand human brains:

Obsessive preoccupation with inappropriate goals.

Inattention and inability to concentrate.

Bad representations.

Excessively broad or narrow generalizations.

Excessive accumulation of useless information.

Superstition; defective credit assignment schema.

Unrealistic cost/benefit analyses.

Unbalanced, fanatical search strategies.

Formation of defective categorizations.

Inability to deal with exceptions to rules.

Improper staging of development, or living in the past.

Unwillingness to acknowledge loss.

Depression or maniacal optimism.

Excessive confusion from cross-coupling.

Seeing that list, one has to wonder, "Can people think?" I suspect there is no simple and magical way to avoid such problems in our new machines; it will require a great deal of research and engineering. I suspect that it is no accident that our human brains themselves contain so many different and specialized brain centers. To suppress the emergence of serious bugs, both those natural systems, and the artificial ones we shall construct, will probably require intricate arrangements of interlocking checks and balances, in which each agency is supervised by several others. Furthermore, each of those other agencies must themselves learn when and how to use the resources available to them. How, for example, should each learning system balance the advantages of immediate gain over those of conservative, long-term growth? When should it favor the accumulating of competence over comprehension? In the large-scale design of our human brains, we still don't yet know much of what all those different organs do, but I'm willing to bet that many of them are largely involved in regulating others so as to keep the system as a whole from frequently falling prey to the sorts of bugs we mentioned above. Until we start building brains ourselves, to learn what bugs are most probable, it may remain hard for us to guess the actual functions of much of that hardware.

There are countless wonders yet to be discovered, in these exciting new fields of research. We can still learn a great many things from experiments, on even the very simplest nets. We'll learn even more from trying to make theories about what we observe in this. And surely, soon, we'll start to prepare for that future art of mind design, by experimenting with societies of nets that embody more structured strategies---and consequently make more progress on the networks that make up our own human minds. And in doing all that, we'll discover how to make symbolic representations that are more adaptable, and connectionist representations that are more expressive.

It is amusing how persistently people express the view that machines based on symbolic representations (as opposed, presumably, to connectionist representations) could never achieve much, or ever be conscious and self- aware. For it is, I maintain, precisely because our brains are still mostly connectionist, that we humans have so little consciousness! And it's also why we're capable of so little functional parallelism of thought---and why we have such limited insight into the nature of our own machinery.

This research was funded over a period of years by the Computer Science Division of the Office of Naval Research.

REFERENCES

Minsky, Marvin, and Seymour Papert [1988], Perceptrons, (2nd edition) MIT Press.

Minsky, Marvin [1987a], The Society of Mind, Simon and Schuster.

Minsky, Marvin [1987b], "Connectionist Models and their Prospects," Introduction to Feldman and Waltz Nov.~23.

Minsky, Marvin [1974], "A Framework for Representing Knowledge," Report AIM--306, Artificial Intelligence Laboratory, Massachusetts Institute of Technology,

Stark, Louise [1990] "Generalized Object Recognition Through Reasoning about Association of Function to Structure", Ph.D. thesis, Dept. of Computer Science and Engineering, University of South Florida, Tampa, Florida