Gravitational Waves: Theoretical
Interpretation
Introduction
General relativity states that gravity is expressed as a space-time
curvature, and it predicts the existence of gravitational waves.
Gravitational waves are propagating gravitational fields produced
by the motion of massive objects. They are often called ripples of
space-time curvature. Gravitational fields produced by massive
particles control the motion of matter or light in space-time in a
manner similar to how electric fields produced by charged particles
control how other charged particles move. It is important to detect
gravitational waves because they would bring new information about
distant galaxies which electromagnetic waves cannot. It could also
directly prove general relativity.
How matter emits gravitational waves
According to General Relativity, when any objects with mass
accelerate, they emit gravitational waves. This is analogous to the
electromagnetic waves emitted by accelerating charged particles.
For example, consider a gravitational wave propagating in the z
direction in Cartesian coordinates. The wave only deforms space-time
in the direction perpendicular to its propagation
direction. Deformation of space-time means shrinking and stretching of
the physical length between two points. Gravitational waves affect
space-time in such a way that certain deformation patterns occur
periodically.
If at time t, space is stretched in the x-direction at the maximum
amplitude, then at time t+T/2 (where T is the period), one-half period
later, space will have shrunk by the maximum amplitude and then will
again stretch to its maximum at time t+T, one full period later. The
theory also states that in the y-direction, space is deformed in the
opposite phase of the x-direction. Thus, if space is stretched out in
the x-direction, space is shrunk in the y-direction.
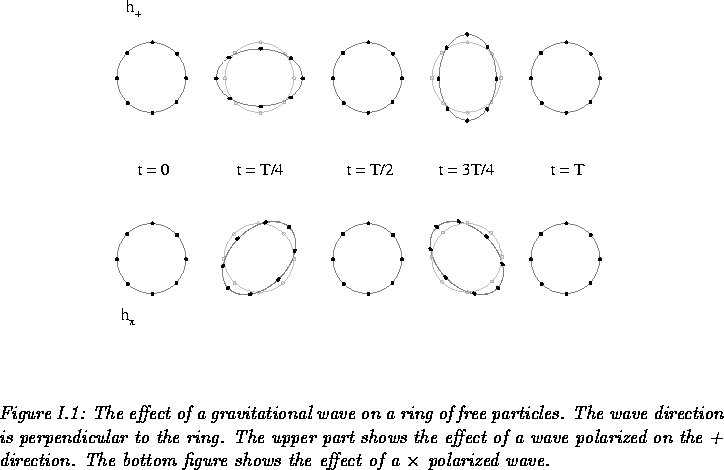
Stretching and Shrinking
The relative length change of two points resulting from
gravitational wave is expressed as
Max stretching & shrinking = hL,
where L is a distance between two points and h is the dimensionless
strain amplitude which is proportional to the second derivative of the
mass distribution of the source and inversely proportional to the
distance from the source. Therefore, the ratio of the stretched length
to the original length is the same for any two points if the
measurements were exercised at the same angle and distance from the
source. However, the longer the original length, the larger the actual
stretching/shrinking effect. This is why interferometers are as large
as 4km and larger ones are being developed. The fact is that motion of
the existing matter in the universe limits h to the range of less than
10^(-21). A 10km interferometer will be able to detect length changes
of 10^(-17)m, which is certainly technically challenging since various
sources of noise make it difficult to distinguish the gravitational
wave. Gravitational waves have not yet been directly detected by this
method.
Sources of detectable gravitational wave
Binary system
The magnitude of the gravitational waves depends on the
distance from the source and the second derivative of the mass
distribution (mass times acceleration in case of one
particle). Thus, one must consider very massive objects moving
violently as the candidates for the sources of detectable
gravitational waves. The most promising candidates are compact
binaries consisting of either two neutron stars, two black holes
or one neutron star and one black hole. They are small and heavy,
which allows them to orbit at a closer distance and at a high
orbital frequency, which means that the second derivative of the
mass distribution of the system is large. Therefore, the system
emits strong gravitational waves. Compact binaries have another
interesting aspect associated with gravitational radiation
(explained in a later section).
Rotating neutron stars
If non axis-symmetric along the rotation axis, a rotating
neutron star will emit gravitational waves. If symmetric, the
second derivative of the mass distribution holds constant at zero
in the system, which leads to no gravitational wave emission.
Supernovae
Supernovae are a good gravitational source. They are compact
and have large accelerations. Similar to rotating neutron stars,
if a supernova's explosion has axial symmetry, gravitational waves
will not be emitted for the constant mass distribution. Initial
density and temperature fluctuations and other factors may direct
asymmetric collapse. If a supernova, which is exceptionally
bright, is observed in gravitational wave, we will be able to test
a prediction of general relativity which states that the speed of
gravitational wave is the same speed as light.

Stochastic background
This comes from the density fluctuation of the early stage of
the universe. Measuring the background would tell us about the
nature of the Plank-size universe and provide clues for testing
the various cosmological models. Although stochastic background is
interesting, it is so weak that modern technology is far from
achieving this task.
Relation between the motion of the source and the period and the
amplitude of the consequent gravitational wave
The magnitude of gravitational waves is proportional to the second
derivative of the mass distribution of the emitting system and
inversely proportional to the separation of the source and observing
point. The next question that arises is how the period of a
gravitational wave is related to that of the motion of the source. If
the binaries are in a circular orbit, the resulting gravitational
waves have a frequency that is twice that of the binary system--that
is, the period of the gravitational wave is one half of the orbital
period.

The magnitude changes with the orientation. However an
angle-averaged estimate of the signal strength is expressed in the
following formula.
missing formula
To see why this is proportional to the second derivative of the
mass distribution of the system, recall that the derivative is
proportional to  and inversely
proportional to
and inversely
proportional to  .
.
This leads to the above equation. Therefore, if the frequency of
the orbital period increases, the resulting gravitational wave will
also increase its frequency and amplitude. And this is achieved by
self-energy loss of gravitational radiation.
Gravitational radiation and self-energy loss of binary system
According to general relativity, gravitational radiation takes
energy from its source. The energy loss results in the smaller
separation of the binaries and therefore shorter orbital
frequency. This comes from the fact that the rate of change in orbital
period of a binary system is negatively proportional to the rate of
change in gravitational potential energy of the binary system:
 ,
,
where m is the gravitational mass of the primary star and M is the
total gravitational mass of the binary system. The gravitational mass
m is the sum of the rest mass and the total self energy of the
gravitating body.
As the system radiates gravitational energy, it decreases its
orbital period. Therefore, the resulting gravitational wave has a
waveform of increasing frequency and amplitude. Furthermore, the
radiation energy is proportional to the square of the amplitude of the
associated gravitational wave. This means that the radiation power
increases faster and faster as the system loses its energy due to
gravitational radiation and thus resulting in the larger rate of
change in orbital period. In fact, the final stage of the binary
system consisting of two neutron stars has such a large radiation
energy that the neutron stars will lose all their potential energy and
finally collide. The waveform resulting from the collision will be
very rough. Looking at the waveform, we can also obtain information
about the mechanism of astronomical events.

Collision of two neutron stars

Binary Neutron Star Merger, calculated by Maximilan
Ruffert

Black Hole - Neutron Star Binary Mergers

Why is it important to measure the gravitational wave?
Gravitational waves are most unique in that they propagate without
interacting with matter. This allows us to obtain new information
about the universe that electromagnetic waves fail to provide. The
amplitude and frequency of gravitational waves describe the frequency
and mass of the emitting source. The shape of the final phase of a
binary system might give some new insight in astronomy. Stochastic
background would reveal the mass distribution of the early plank-scale
universe and the evolution of the early universe.




 and inversely
proportional to
and inversely
proportional to  .
. ,
,



