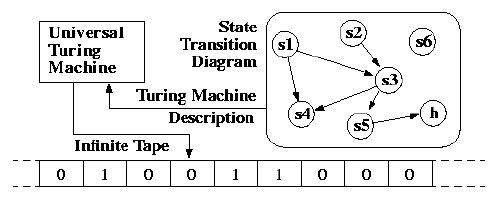
A Turing Machine is the mathematical tool equivalent to a digital computer. It was suggested by the mathematician Turing in the 30s, and has been since then the most widely used model of computation in computability and complexity theory.
The model consists of an input output relation that the machine computes. The input is given in binary form on the machine's tape, and the output consists of the contents of the tape when the machine halts.
What determines how the contents of the tape change is a finite state machine (or FSM, also called a finite automaton) inside the Turing Machine. The FSM is determined by the number of states it has, and the transitions between them.
At every step, the current state and the character read on the tape determine the next state the FSM will be in, the character that the machine will output on the tape (possibly the one read, leaving the contents unchanged), and which direction the head moves in, left or right.
The problem with Turing Machines is that a different one must be constructed for every new computation to be performed, for every input output relation.
This is why we instroduce the notion of a universal turing machine
(UTM), which along with the input on the tape, takes in the
description of a machine M. The UTM can go on then to simulate M on
the rest of the contents of the input tape. A universal turing machine
can thus simulate any other machine.

I learned about Turing Machines the first term of my sophomore year at MIT (Fall 96), in 6.004 (Computational Structures), the best class ever conceived. It was late one night when I was starting my problem set on writing a turing machine to compute some operation. To test my result, I figured I could code up a Universal Turing Machine in Scheme to help me do my problem set. I could then feed it my description and a sample input, and it would simulate any machine for me. To my surprise within two hours, the program was working, and i could start the rest of my problem set (You can read on, or simply download the scheme code).
;;
;; 10/22/96 3am-5am: Manolis Kamvysselis - manoli@mit.edu
;;
;; Program used to check solutions to a 6.004 problem set
;; Simulation of a Turing machine
;; global variables used by procedures.
;; Those are changed at every step, and must be reinitialized before running a different
;; example, by running: (setup state-graph tape initial-state initial-position)
(define *machine* '()) ; the machine currently running
(define *state* 's1) ; the state at which the current machine is at
(define *position* 0) ; the position at which the tape is reading
(define *tape* #()) ; the tape that the current machine is currently running on
;; The following procedure takes in a state graph (see examples below), and turns it
;; to a machine, where each state is represented only once, in a list containing:
;; a structure of the form:
;; ((state (in out move next-state) (in out move next-state) (in out move next-state))
;; (state2 (in out move next-state))
;; (state3 (in out move next-state) (in out move next-state)))
;;
;; Each state name is followed by a list of combinations of inputs (read on the tape)
;; and the corresponding output (written on the tape), direction of motion (left or right),
;; and next state the machine will be in.
;;
;; Here's the machine returned by (initialize flip) (as defined at the end of this file)
;;
;; ((s4 (0 0 l h))
;; (s3 (1 1 r s4) (0 0 l s3))
;; (s2 (0 1 l s3) (1 0 r s2))
;; (s1 (0 1 r s2) (1 1 l s1)))
(define (initialize state-graph)
(define (extend machine states-to-go)
(if (null? states-to-go)
machine
(let ((cur-state (first states-to-go))
(matched #f))
(extend (begin (for-each (lambda (state)
(if (equal? (state-name state) (car cur-state))
(begin (set! matched #t)
(set-cdr! state (cons (cdr cur-state) (cdr state))))))
machine)
(if matched
machine
(cons (list (state-name cur-state)
(cdr cur-state))
machine)))
(cdr states-to-go)))))
(extend '() state-graph))
;; Setup is a handy procedure to initialize and test a new graph.
;; It will take care of reading the graph, and initializing the global variables.
;; Once this is done, all one has to do is run the program (run) or move step
;; by step (step) for debugging
(define (setup state-graph tape state position)
(set! *machine* (initialize state-graph))
(set! *tape* tape)
(set! *state* state)
(set! *position* position))
;; The following are the procedures that implement the Turing machine.
;; It can write, read, move, etc...
(define (set-state! state)
(set! *state* state))
(define (set-position! position)
(set! *position* position))
(define (do-move move-to-make)
(cond ((equal? move-to-make 'R) (move-right))
((equal? move-to-make 'L) (move-left))
(else (error "i don't know what move to make: " move-to-make))))
(define (move-right)
(set! *position* (+ *position* 1)))
(define (move-left)
(set! *position* (- *position* 1)))
(define (write output)
(vector-set! *tape* *position* output))
(define (read)
(vector-ref *tape* *position*))
;; The following Constructors and selectors implement the data
;; structures used by the program.
;; A State is: '(s1 (0 1 r s2) (1 1 l s1))
;; (see above)
(define state-name car)
(define state-specs cdr) ;; returns ==> '((0 1 r s2) (1 1 l s1))
;; (a list of specs)
;; spec is: (input output move next-state)
;; It specifies for a given input, the output, direction of motion and
;; next state.
(define spec-input car)
(define spec-result cdr)
;; result is: (output move next-state)
;; These are all the things we have to deduce from state and input,
;; to be able to continue in our program.
(define result-output car)
(define result-move cadr)
(define result-state caddr)
;; This procedure looks through our *machine* to find the state
;; whose name it is given, and it returns the state with all
;; of its specifications.
(define (get-state-by-name name)
(define (helper states-to-go)
(if (null? states-to-go)
(error "Reference to undefined state" name)
(if (equal? (state-name (car states-to-go)) name)
(car states-to-go)
(helper (cdr states-to-go)))))
(helper *machine*))
;; This procedure is called with the output from the previous procedure (a state)
;; and an input (read from the tape), and it returns the actions to perform
;; (what to write, where to move, which state to go to), in the form:
;; (current-state (output direction-of-motion next-state))
(define (get-what-to-do state input)
(define (helper specs-to-go input)
(if (null? specs-to-go)
(error "Unspecified input to state encountered\n You haven't told me what to do in state"
(state-name state) 'with 'input input)
(if (equal? (spec-input (car specs-to-go)) input)
(list (state-name state) (spec-result (car specs-to-go)))
(helper (cdr specs-to-go) input))))
(helper (state-specs state) input))
;; example:
;; (get-what-to-do (get-state-by-name 's1) 0)
;; ;Value: (s1 (1 r s2))
;; the following selectors deal with the output of get-what-to-do
;; what-to-do is of the form: (current-state (output move next-state))
(define what-to-output caadr)
(define where-to-move cadadr)
(define (what-next-state what-to-do)
(car (cddadr what-to-do)))
;; Sending output (for the user to know what's going on)
(define (describe-move input output move state)
(newline)
(display (list 'input: input 'output: output 'move: move 'state: state 'position: *position* ':
(read))))
(define (describe-current-position)
(newline)
(display (list *tape* *state* *position* (read))))
(define (return-current-position)
(list *tape* *position* *state*))
;; and here are the procedures that make everything work
;; Once the global variables are set appropriately (either automatically by
;; running (setup ...) or manually (for debugging), calling the procedure
;; (step) will make the Turing machine perform one action.
(define (step)
(let* ((what-to-do (get-what-to-do (get-state-by-name *state*) (read)))
(output (what-to-output what-to-do))
(move (where-to-move what-to-do))
(state (what-next-state what-to-do)))
; (describe-move input result output move state)
(write output)
(do-move move)
(set-state! state)
(describe-current-position)))
;; All (run) is doing is calling (step) until the state is "halt" (here 'h)
(define (run)
(if (equal? *state* 'h)
(return-current-position)
(begin (step) (run))))
;; And here are the actual tests relevant to the problem set
;; flip flips a unary number 01111110 to 10000001.
(define flip
'(
(s1 1 1 L s1)
(s1 0 1 R s2)
(s2 1 0 R s2)
(s2 0 1 L s3)
(s3 0 0 L s3)
(s3 1 1 R s4)
(s4 0 0 L H)))
(define tape1
(list->vector '(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _)))
;; We will run the test on tape1 (above), starting in state s1, and in position 17 of the tape (arbitrary choice)
(setup flip tape1 's1 17)
(run)
;; Here's the output:
;; (i've taken the liberty of erasing the lines where the pointer only was moving, without changing the
;; inputs, outputs, state, but only the position on the tape (as you can notice on the rightmost part of the output).
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s1 16)
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s1 7)
;; (#(_ _ _ _ _ _ _ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 8)
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 9)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 10)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 11)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 12)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 13)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 14)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 15)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 16)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 17)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 18)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 19)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 20)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 21)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 22)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 23)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 24)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 25)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 26)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s3 25)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s3 7)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s4 8)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) h 7)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) h 7)
;Value: (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) 7 h)
;; this is the second A of problem 1
;; It takes a unary number, and doubles it: 011110 -> 0111111110
(define doubler
'(
(s1 1 1 L s1)
(s1 0 1 R s2)
(s2 1 0 R s3)
(s2 0 0 L s8)
(s3 0 0 R s4)
(s3 1 1 R s3)
(s4 _ 1 L s5)
(s4 1 1 R s4)
(s5 0 0 L s6)
(s5 1 1 L s5)
(s6 0 0 R s8)
(s6 1 1 L s7)
(s7 0 0 R s2)
(s7 1 1 L s7)
(s8 0 0 R s8)
(s8 1 0 R s8)
(s8 _ 0 L s9)
(s9 0 0 L s10)
(s10 0 1 L s10)
(s10 1 0 R s11)
(s11 0 0 L H)
(s11 1 1 L H)))
(define tape2
(list->vector '(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _)))
(setup doubler tape2 's1 11)
(run)
;; Here's the output (with the same criteria as above for erasing lines).
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _) s1 10 1)
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _) s1 7 0)
;; (#(_ _ _ _ _ _ _ 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _) s2 8 1)
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _) s3 9 1
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _) s4 15 _)
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 0 1 _ _ _ _ _ _ _ _ _ _) s5 14 0)
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 0 1 _ _ _ _ _ _ _ _ _ _) s2 9 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 0 1 _ _ _ _ _ _ _ _ _ _) s3 10 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 0 1 _ _ _ _ _ _ _ _ _ _) s4 16 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 0 1 1 _ _ _ _ _ _ _ _ _) s5 15 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 0 1 1 _ _ _ _ _ _ _ _ _) s2 10 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 0 1 1 _ _ _ _ _ _ _ _ _) s3 11 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 0 1 1 _ _ _ _ _ _ _ _ _) s4 17 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 0 1 1 1 _ _ _ _ _ _ _ _) s5 16 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 0 1 1 1 _ _ _ _ _ _ _ _) s2 11 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 0 1 1 1 _ _ _ _ _ _ _ _) s3 12 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 0 1 1 1 _ _ _ _ _ _ _ _) s4 18 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 0 1 1 1 1 _ _ _ _ _ _ _) s5 17 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 0 1 1 1 1 _ _ _ _ _ _ _) s2 12 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 0 1 1 1 1 _ _ _ _ _ _ _) s3 13 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 0 1 1 1 1 _ _ _ _ _ _ _) s4 19 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 0 1 1 1 1 1 _ _ _ _ _ _) s5 18 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 0 1 1 1 1 1 _ _ _ _ _ _) s2 13 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 _ _ _ _ _ _) s3 14 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 _ _ _ _ _ _) s4 20 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 1 _ _ _ _ _) s5 19 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 1 _ _ _ _ _) s8 15 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 1 1 1 1 1 _ _ _ _ _) s8 16 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 1 1 1 1 _ _ _ _ _) s8 17 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 1 1 1 _ _ _ _ _) s8 18 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 1 1 _ _ _ _ _) s8 19 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _) s8 20 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 _ _ _ _ _) s8 21 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 _ _ _ _) s9 20 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 _ _ _ _) s10 19 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 _ _ _ _) s10 18 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 _ _ _ _) s10 17 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 _ _ _ _) s10 16 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 1 1 1 1 0 0 _ _ _ _) s10 15 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 0 0 _ _ _ _) s10 14 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 1 1 1 1 1 1 0 0 _ _ _ _) s10 13 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 12 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 11 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 10 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 9 0)
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 8 0)
;; (#(_ _ _ _ _ _ _ 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 7 1)
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s11 8 1)
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) h 7 0)
;; ;Value: (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) 7 h)