User’s Guide: Chapter 17: Derivations¶
Suppose you have a music21 score that was organized something like
this:
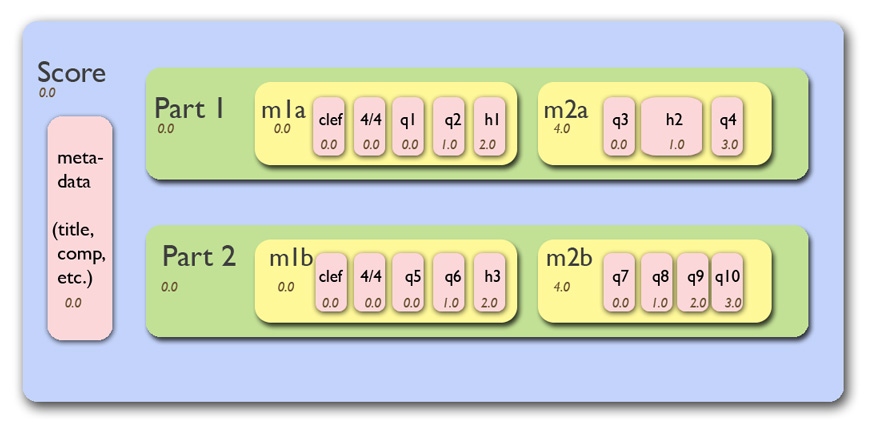
Figure 17.1: Score hierarchy¶
What we’ve seen already is that iterating over the score via,
for n in score: print n will only get you the highest level of
objects, namely the Metadata object and the two Part objects.
The inner objects, measures, clefs, notes, etc. Will not be available.
The simplest way of getting at all these objects is with the
Stream.flatten() method. Calling it on this score will change the
representation so that only the non-stream elements (the pink ovals)
remain in the score:
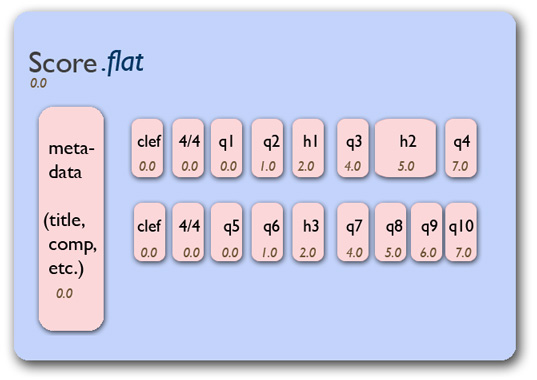
Figure 17.2: Flat Score¶
This should be a review from previous chapters in the User’s Guide. This
section explains the relationship between the original stream.Score
object, which we will call s, and the flattened representation,
which we will call s.flat or sf. The relationship between the
two is called a Derivation. Symbolically, this representation can be
visualized as follows:
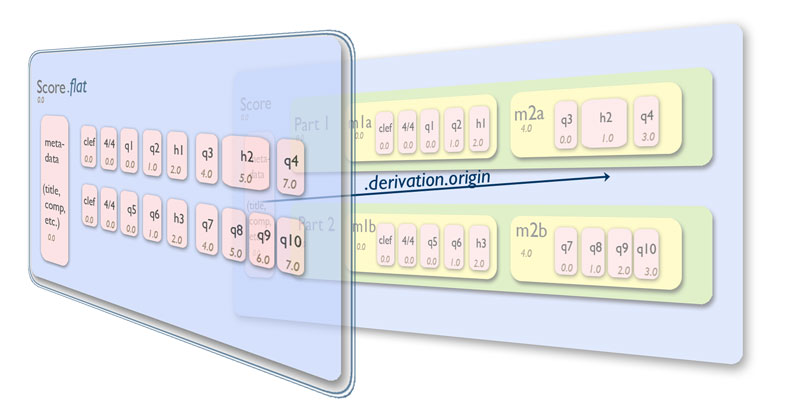
Figure 17.3: Derivation representation¶
Let’s parse a Mozart string quartet, K. 80, give it an ID and look where it came from:
from music21 import *
s = corpus.parse('mozart/k80', 1)
s.id = 'mozartK80'
s.derivation
<Derivation of <music21.stream.Score mozartK80> from None>
This Score is the first Stream representing this piece in music21 so it
has no derivation origin. However, let’s look at the first couple of
measures of the piece using .measures:
sExcerpt = s.measures(1, 4)
sExcerpt.id = 'excerpt'
sExcerpt.show()

This excerpt has a more interesting .derivation:
sExcerpt.derivation
<Derivation of <music21.stream.Score excerpt> from <music21.stream.Score mozartK80> via 'measures'>
There are three things that are reported by the __repr__ of the
Derivation object: the client (that is
the element housing the Derivation object), the origin (that is the
Stream that the client was derived from), and the method that derived
the new Stream:
sExcerpt.derivation.client
<music21.stream.Score excerpt>
sExcerpt.derivation.origin
<music21.stream.Score mozartK80>
sExcerpt.derivation.method
'measures'
Let’s create another Stream from the Excerpt, this time, via transposition:
sTransposed = sExcerpt.transpose('P4')
sTransposed.show()

sTransposed.id = 'transposed'
sTransposed.derivation
<Derivation of <music21.stream.Score transposed> from <music21.stream.Score excerpt> via 'transpose'>
sTransposed.derivation.method
'transpose'
Now this Stream has an origin, and that Stream has an origin. If we
wanted to know where everything came from, we can use the
.rootDerivation property:
sTransposed.derivation.origin
<music21.stream.Score excerpt>
sTransposed.derivation.origin.derivation.origin
<music21.stream.Score mozartK80>
sTransposed.derivation.rootDerivation
<music21.stream.Score mozartK80>
If we want to know the whole history of where this Stream comes from, we
can use the .chain() method on the Derivation object:
for previousScore in sTransposed.derivation.chain():
print(previousScore)
<music21.stream.Score excerpt>
<music21.stream.Score mozartK80>
Note that derived Streams retain information about where they came from, but not vice-versa: there’s no way to go from the original “mozartK80” Stream back to the “transposed” Stream.
There are good uses for the derivation chain. For instance, what if we
want to change every piano mark to a forte, we might define a
function to do that on a Stream and then call it on sTransposed:
def makeLouder(s):
for dyn in s.recurse().getElementsByClass('Dynamic'):
dyn.value = 'f'
makeLouder(sTransposed)
sTransposed.show()

That’s pretty cool, but our original score is unchanged:
sExcerpt.show()

So, if we want to backtrack up the history of the score, let’s call
makeLouder on each Score in the .derivation.chain() (and now you
might see why we make makeLouder a function to begin with:)
for s in sTransposed.derivation.chain():
makeLouder(s)
sExcerpt.show()

I hope that this gave a sense not only what Derviations are, but also why you might use them. We’ll continue to use derivations in later chapters, but for now let’s return to some fundamentals of music theory in the form of Intervals, in Chapter 18.