(1) I will find the red books.
We have lots of evidence that a sentence like this one isn't just a string of words. In particular, there are sequences of words in this sentence which have a privileged status, as objects that syntactic operations get to manipulate; we call these privileged strings of words constituents. Consider the conditions on topicalization, for example:
(2) The red books, I will find.
(3) (I said I would find the red books, and...) find the red books, I will.
(4) *find the red, I will books.
The data above offer us one argument that the red books and find the red books are constituents, and that find the red is not a constituent. Several other phenomena seem to point in the same direction. Here are data involving a construction called pseudoclefting:
(5) What I will find is the red books
(6) What I will do is find the red books
(7) *What I will do books is find the red
The constituents the red books and find the red books can appear at the end of a pseudocleft, after is, but we can't put find the red in a pseudocleft. Another argument for the same conclusion comes from the properties of sentence fragments; if I'm surprised by your claim that you will find the red books, I might utter the first two sentence fragments below, but not the third one:
(8) the red books?!
(9) find the red books?!
(10) *find the red?!
Similarly, the first two sentence fragments above (minus the "?!" at the end) can be answers to questions (specifically, to the questions What did you find? and What will you do?, respectively), but there's no question that could have the third sentence fragment above as its answer (well, apart from metalinguistic questions like What are the third, fourth, and fifth words of this sentence?, which we'll ignore).
When we consider the strings that may be substituted for the red books in our example sentence to yield well-formed sentences, we find that they all contain at least one noun:
(11) I will find the red books
(12) I will find the books
(13) I will find books
(14) *I will find the
(15) *I will find red
It appears that the noun books is the crucial part of the phrase the red books that makes it capable of appearing where it does in the sentence. So we'll name the phrase a noun phrase (or NP), to reflect the importance of the noun. Now we need a name for find the red books, and the only word in that that isn't also in the noun phrase the red books is the verb find, so we'll call that one a verb phrase (VP).
In all the examples we've been considering, I is also an NP. We can replace it with things that resemble the NPs we've already seen:
(16) The tall men will find books.
(17) The men will find books.
(18) Men will find books.
(19) *The will find books.
(20) *Tall will find books.
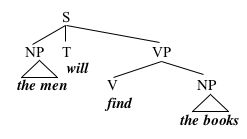
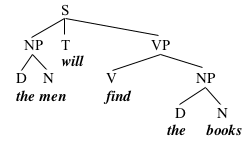
We can represent the theory that we've built so far in a diagram like this one:

Diagrams like this are called trees (or sometimes phrase structure trees). This particular tree represents the fact that the men and the books are NPs, by connecting those strings of words to nodes labelled 'NP', via lines pointing down. Similarly, the tree notes that find the books is a VP, since the node VP is connected to those words via lines pointing down. It also labels the word will with T (for Tense), and declares the whole thing to be a Sentence (S).
This tree gives part of the internal structure of its VP, which it says consists of a V, find, along with an NP, the books. It doesn't give the internal structure of either NP; instead, each NP has a triangle under it, which is simply a convention for structure that we don't yet wish to diagram fully.
Just to develop some terminology, we will say that when one node is connected to another node via a line, the higher node in the tree immediately dominates the lower node. In this tree, for example, the node S immediately dominates the nodes NP, T, and VP, and the node VP immediately dominates the nodes V and NP. We will also use the term dominate, which is just the transitive closure of immediately dominate; X dominates Y if X immediately dominates Y, or if X immediately dominates some Z which dominates Y. In this tree, for example, S dominates NP, T, VP, V, and NP.
Another way of talking about trees is in terms of feminine kinship relations; if X immediately dominates Y, we say that X is the mother of Y, and that Y is the daughter of X. Two nodes that have the same mother are sisters. In the tree under consideration here, for example, VP is the mother of V and NP, and V and NP are therefore sisters.
Returning to the tree we've been looking at; how would we generate it? One way would be to create some rules which state explicitly the recipes for constructing phrases of various kinds. Rules of the relevant type, called phrase structure rules, are given below:
S→NP T VP
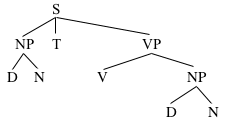
NP→D N
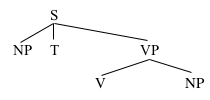
VP→V NP
These phrase structure rules say things like "S immediately dominates NP, T, and VP". The order in which the rules are stated here is unimportant, but as it happens, the first rule is a good one to start with; you can begin creating a tree by introducing an S, which immediately dominates NP, T, and VP:
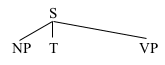
For your next trick, referring to our third phrase structure rule, you can make the VP immediately dominate V and NP:
And, finally, you can make each NP consist of a D and an N:
All we need now is a lexicon telling us which words count as instances of N, V, and so on, and we're in a position to diagram simple sentences:
N=men, books...
V=read, find...
T=will...
D=the, an...
We can refer to this toy lexicon for English to turn the tree we've constructed into a sentence, by adding words of the appropriate types under each node, like so:
Now, parts of the outputs of some of these rules seem to be optional. For instance, we have a rule for verb phrases which states that verb phrases always consist of a verb followed by a noun phrase. But we know that this isn't true:
(21) John ate.
(22) John ate lunch.
(23) John ate lunch in the restaurant.
So our VP rule apparently needs some work. In order to handle the first two sentences above, we need to make the NP part of VP optional. And in order to deal with the last one, we need to introduce a new kind of phrase, the PP (Prepositional Phrase), which is also an optional part of the VP:
VP→V NP (NP) (PP)
PP→P NP
The PP can also be a part of NP:
(24) John left.
(25) The man left.
(26) The tall man left.
(27) The tall man in the yellow hat left.
So we need to fix our NP rule as well, like so:
NP→(D) (A) N (PP)
Now, even without getting any further than this, we're already in a position to capture a couple of properties of language. For one thing, we can explain certain cases of ambiguity. A sentence like the following, for example, is ambiguous:
(28) I will hit the fly with the newspaper
This sentence has the normal reading, in which I will use a newspaper to hit the fly, and also a silly reading in which I will hit (maybe with my hand) a fly that is reading a newspaper. As it happens, the theory we've put together so far has two places to introduce PP's, with the result that this sentence can be diagrammed in two different ways:
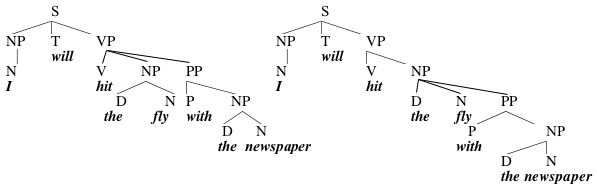
These trees differ in the placement of the PP with the newspaper; this PP either modifies the VP, expressing how the action will be performed (i.e., that I will do the hitting with a newspaper), or the NP the fly, in which case it describes the fly (as having a newspaper). What we now predict is that if we run constituency tests that distinguish between the two structures, the ambiguity ought to collapse. This seems to be true:
(29) What I will hit is the fly with the newspaper.
(30) The fly with the newspaper, I will hit.
These examples only have the odd reading in which it is the fly who has the newspaper. And this is what we expect, because these are examples that must crucially be related to the tree on the right, in which the fly with the newspaper is a constituent, and in which with the newspaper modifies fly.
So this type of ambiguity, at least, seems to be captured by our system. Another property of language which our system captures is its ability to generate potentially infinitely long sentences (remember?). Note that, for example, one of the ingredients of PP is an NP, and that one of the possible ingredients of an NP is a PP. This allows us to generate trees like:
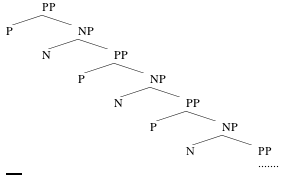
Consequently, there is no upper bound, as far as the grammar is concerned, to the length of a sentence that could start like:
(31) I will hit the fly with a magazine with a cover with art from a country from the continent with the largest island on a lake on an island on...
So, primitive though this system is, it captures some of our intuitions about constituent structure, and about ambiguity, and about the arbitrary length of sentences.