IEC Fusion Reactor Simulator - Autonomous PID Control with GA

Project Overview

Inertial Electrostatic Confinement (IEC) fusion reactors rely on carefully controlled electric fields and pressures to achieve and maintain plasma conditions suitable for fusion reactions. Managing these conditions autonomously is a complex task. This project simulates an IEC reactor environment and trains a PID controller using a genetic algorithm (GA) to achieve stable, targeted voltages and plasma conditions without human intervention.

The ultimate goal is to transfer this simulation-trained, GA-optimized PID controller to a real IEC reactor to allow fully autonomous control.

Simulation Parameters

The simulation environment models gas pressures, fuel flow rates, valve positions, and reactor voltage responses. It includes optional plasma disruptions and voltage fluctuations. The PID controller adjusts Mass Flow Controller (MFC) flow rates and a valve position to stabilize the reactor at a desired voltage setpoint, compensating for dynamic changes.

PID Control Equations

A Proportional-Integral-Derivative (PID) controller is used to regulate the reactor conditions. The control signal $ u(t) $ is computed from the error $ e(t) = V_{\text{desired}}(t) - V_{\text{measured}}(t) $ as follows:

$$ u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{d}{dt}e(t) $$

where

$K_p$: Proportional gain

$K_i$: Integral gain

$K_d$: Derivative gain

By tuning $ K_p, K_i, $ and $ K_d $ appropriately, the PID controller can minimize the voltage error over time. However, manual tuning for such a complex and noisy environment is challenging, hence the use of a genetic algorithm.

Genetic Algorithm Optimization

The genetic algorithm (GA) is employed to automatically find optimal PID gains by simulating multiple controller configurations, evaluating their performance, and then evolving the population towards better solutions.

Each individual in the population corresponds to a set of PID gains:

$$ \{K_{p,\text{MFC}}, K_{i,\text{MFC}}, K_{d,\text{MFC}}, K_{p,\text{BVP}}, K_{i,\text{BVP}}, K_{d,\text{BVP}}\} $$

A fitness function $ F $ evaluates how well a given set of PID parameters performs based on criteria such as voltage error, overshoot, fuel usage, and purity:

$$ F = w_{\text{error}}E + w_{\text{fuel}}F_{usage} + w_{\text{over}}O_{v} + w_{\text{overshoot}}O_{s} + w_{\text{oscillations}}Z + w_{\text{purity}}P_{low} + w_{\text{ISE}} \int_0^T e(t)^2 dt $$

where

$E$: Average absolute voltage error

$F_{usage}$: Total fuel consumption

$O_{v}$: Over-voltage penalty

$O_{s}$: Overshoot penalty

$Z$: Oscillation measure (e.g., zero-crossings of the error)

$P_{low}$: Low purity penalty

ISE: Integral of squared error

$w_*$: Corresponding weighting factors

The GA uses selection, crossover, and mutation operations to evolve the population:

- Initialize population with random PID parameters

- Evaluate fitness of each individual

- Select top performers and apply crossover to produce offspring

- Mutate some offspring for diversity

- Repeat for multiple generations until convergence

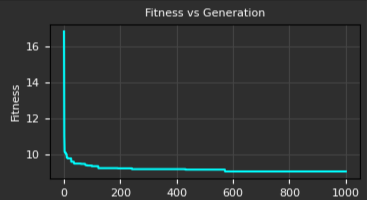
The genetic algorithm typically converges within 600 generations, allowing for rapid experimentation with different reward function weightings. This quick convergence enables iterative refinement of the fitness criteria to achieve desired control characteristics. The adjacent graph shows how the population's average and best fitness scores stabilize, indicating successful optimization of the PID parameters.

Graph showing genetic algorithm fitness convergence over generations — GA fitness convergence over generations

Before and After GA Optimization

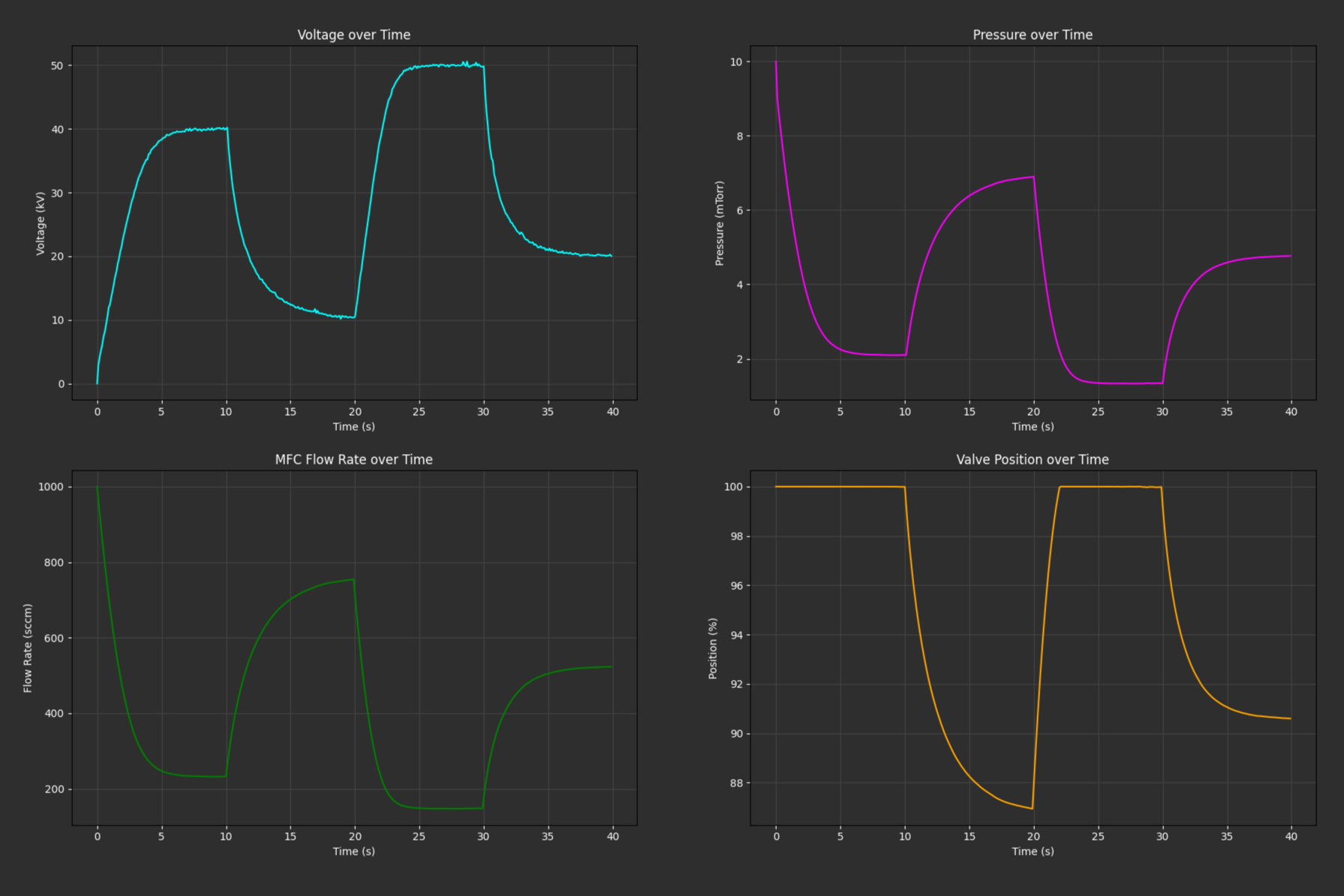
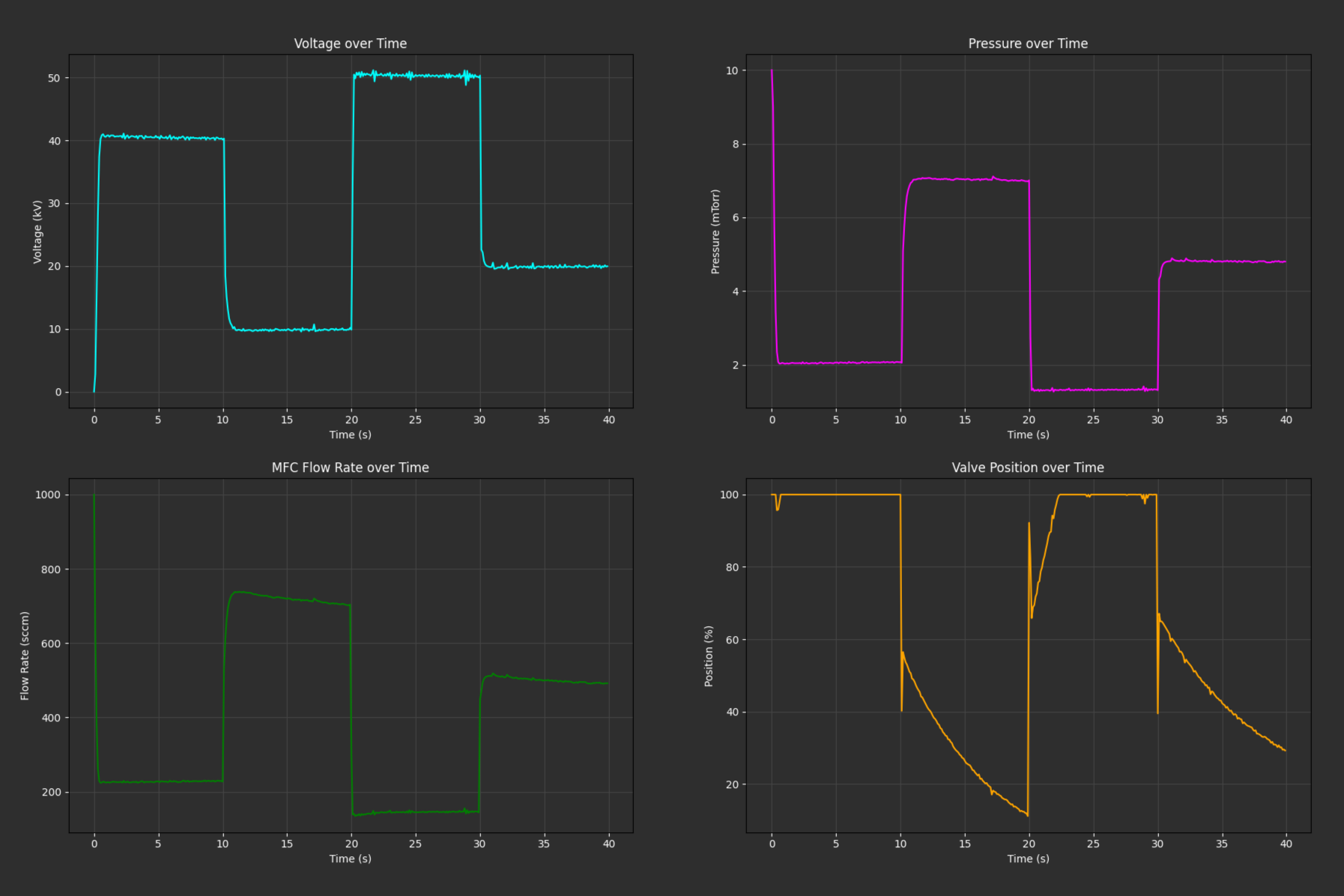
The following images showcase the PID controller performance before and after the GA optimization. Initially, the controller may struggle with large overshoots and settling times. After training with the GA, the PID parameters are tuned for better stability and lower steady-state error.

Pre-optimized PID Controller showing high oscillations and poor settling time — Voltage response before GA optimization, exhibiting significantly slow settling time

GA-Optimized PID Controller showing improved stability and faster settling — Voltage response after GA optimization, demonstrating faster convergence to setpoint

Future Work

Future developments include refining the physical realism of the simulation and deploying the GA-tuned PID controller on a physical IEC reactor. By continually improving the fidelity of the simulation and optimization algorithms, the system will be better prepared to handle the complexities and uncertainties of real experimental conditions.