First, follow all of the directions you were given. (See maps below).
All of these paths are constructible with simple tools: rhumb lines by literally drawing straight lines on a Mercator map, great circles using an online great circle plotter, the tetrahedron with some spherical trigonometry. Google Earth is also helpful, and of course some GIS programming can guide you around (although you probably still want to hand-evaluate many country shape properties.).
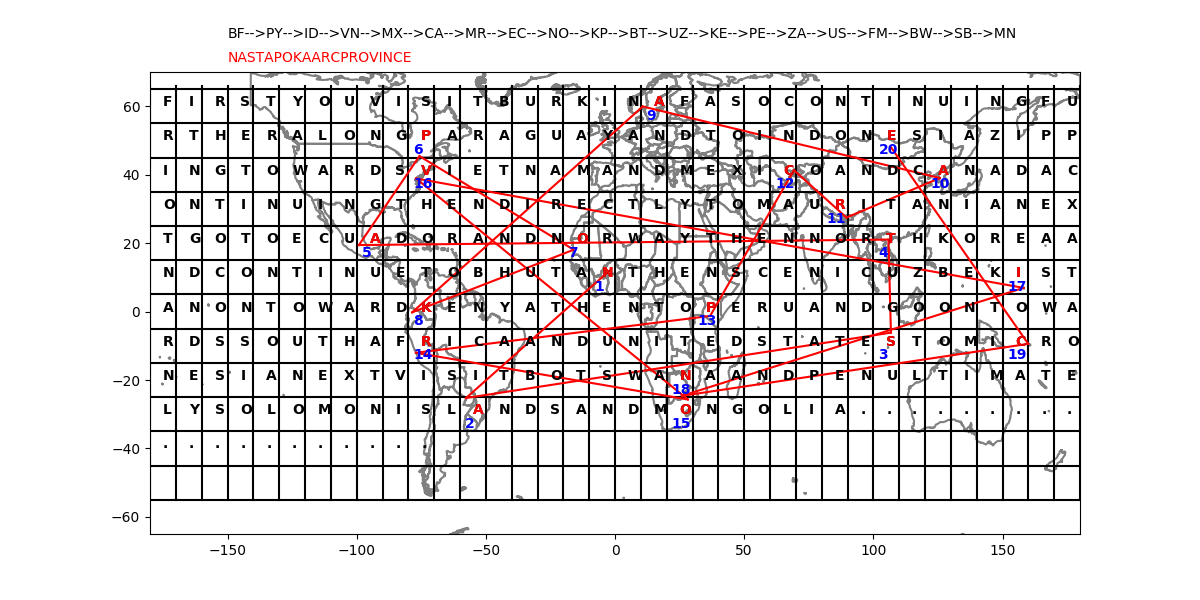
If you've solved the map navigation clues correctly, you can fill in the blanks in the telegram:
First you visit Burkina Faso continuing further along Paraguay and to Indonesia zipping towards Vietnam and Mexico and Canada continuing then directly to Mauritania next go to Ecuador and Norway then North Korea and continue to Bhutan then scenic Uzbekistan on toward Kenya then to Peru and go on towards South Africa and United States to Micronesia next visit Botswana and penultimately Solomon Islands and Mongolia
You should have noticed that the blank telegram has a grid on it, labeled as though it’s a map with a 10×10 degree “boxes” starting at 65N, 180W.
If you write the telegram in there, one letter per box, you’ll be able to associate any latitude and longitude with one letter of the message.
The voyage takes you to each country's capital, so read off the map-letter that overlaps each capital you visited. For example, Burkina Faso's capital, Ouagadougou, is at about 12N 1W, and therefore lies in the grid square where you've written the N in BHUTAN.
Read off the letter associated with each capital, in voyage order, to get NASTAPOKA ARC PROVINCE.
The Nastapoka Arc is a remarkable semicircular feature in the Hudson Bay coastline of a Canadian province, one you could get to from MIT in three and a half hours (rather less time than you probably spent getting to the answer to this puzzle), namely QUEBEC.
- CLUE: Start in Burkina Faso.
DESTINATION: Burkina Faso
DESTINATION CAPITAL COORDINATES: [12.37, -1.52]
READOUT LETTER: N from “Bhutan”
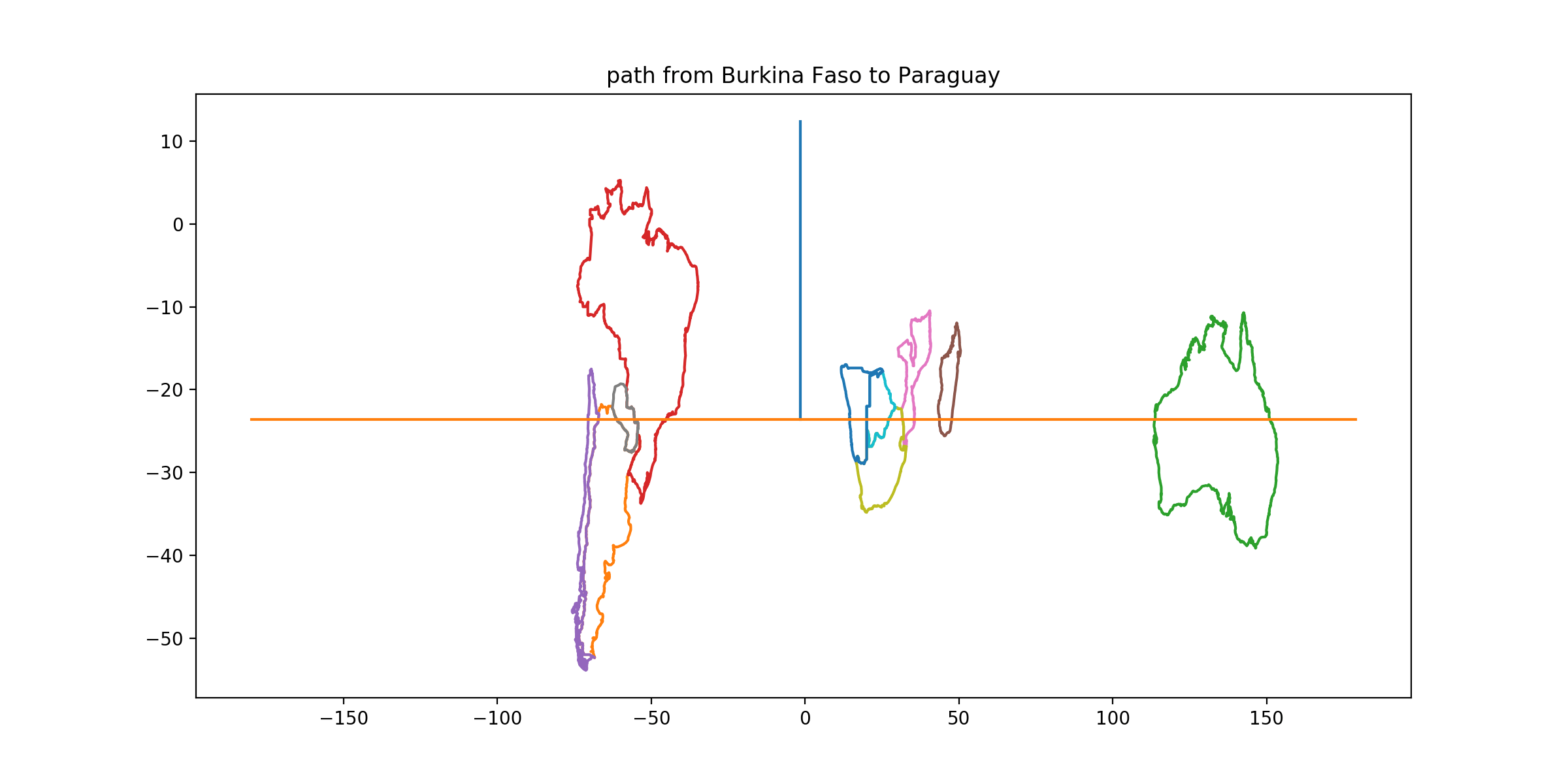
SOLUTION: The capital of Burkina Faso is Ouagadougou. - CLUE: From its capital[1], go south 36 degrees. Travel in latitude until you reach a country[2] whose entire land area[3] is inside the convex hull[4] of another country’s capital territory[5].
DESTINATION: Paraguay
DESTINATION CAPITAL COORDINATES: [-25.27, -57.67]
READOUT LETTER: A from “Solomon Islands”
SOLUTION: Paraguay is entirely enclosed in a line stretched around Brazil.
- CLUE: From its capital, follow a great circle initially heading north or south. For each contiguous territory[6] you encounter, draw the largest possible circle that contains only seawater and which lies within the territory’s convex hull, and draw the largest possible circle containing only land. Stop in the territory for which the water-circle radius is the largest fraction of the land-circle radius. (You should find yourself in a non-capital-territory where the large seawater circle did not touch the convex hull at all.)
DESTINATION: Indonesia
DESTINATION CAPITAL COORDINATES: [-6.17, 106.82]
READOUT LETTER: S from “United States”
SOLUTION: Going over the pole and back down, this route takes you through many non-capital-territory islands—Newfoundland, Greenland, numerous Philippine islands, and Sulawesi in Indonesia. In Sulawesi, the Gulf of Tomini admits a circle very nearly the same size as the largest one that fits in the deeply-indented central land. Luzon comes close, Mindanao not so close.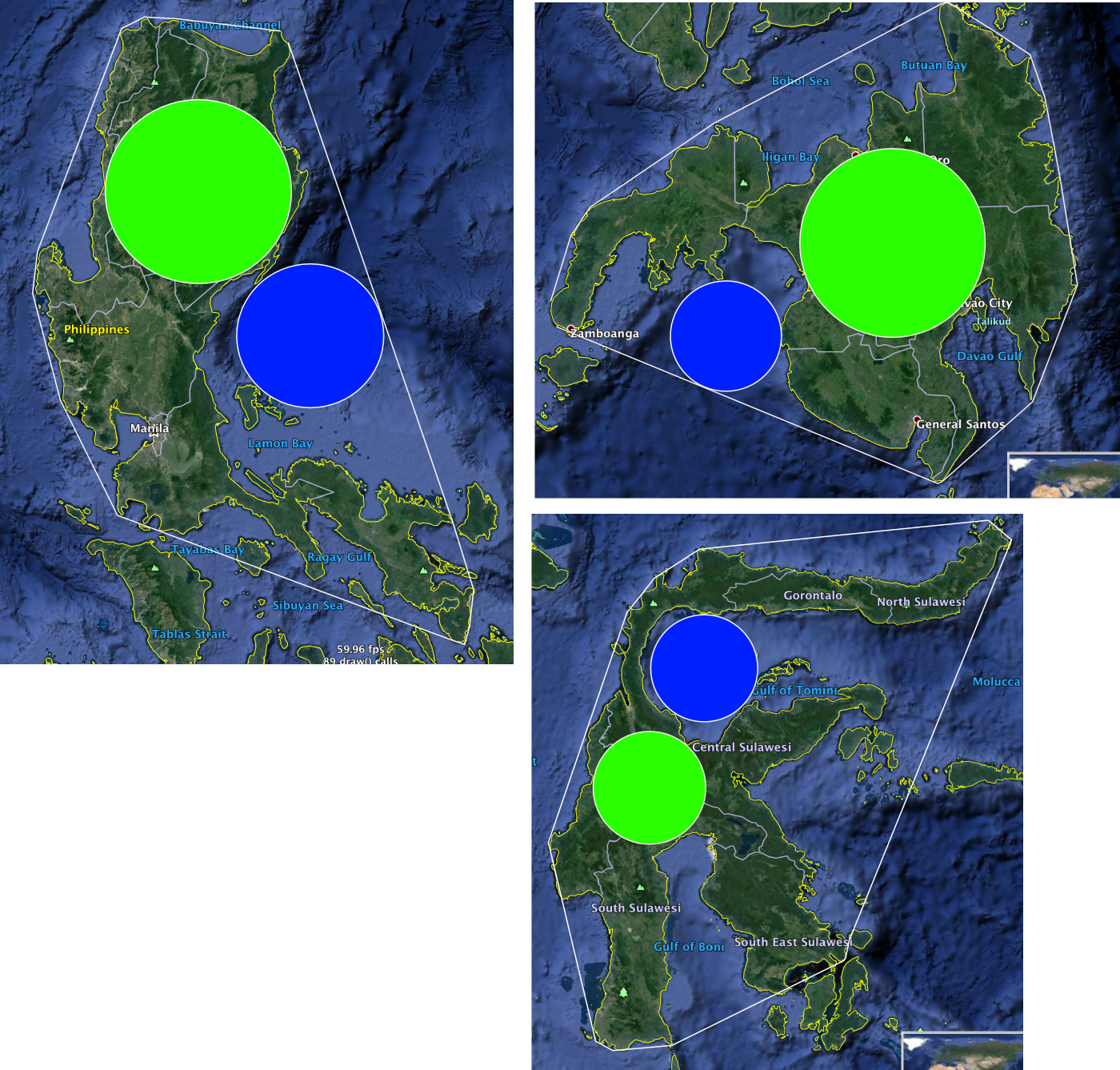
-
CLUE: From its capital, find the capital territory at the same longitude whose land area can be bisected by the relatively shortest[7] straight line.
DESTINATION: Vietnam
DESTINATION CAPITAL COORDINATES: [21.03, 105.85]
READOUT LETTER: N from “North Korea”
SOLUTION: Vietnam has a very narrow ‘waist’; it can be sliced in half by a line about 40 km long somewhere north of Huế. 40/sqrt(331698) is our measure of the ‘relative shortness’ of this bisector. (The next closest case, Laos, has a relative bisector length of about 60/sqrt(238000))
-
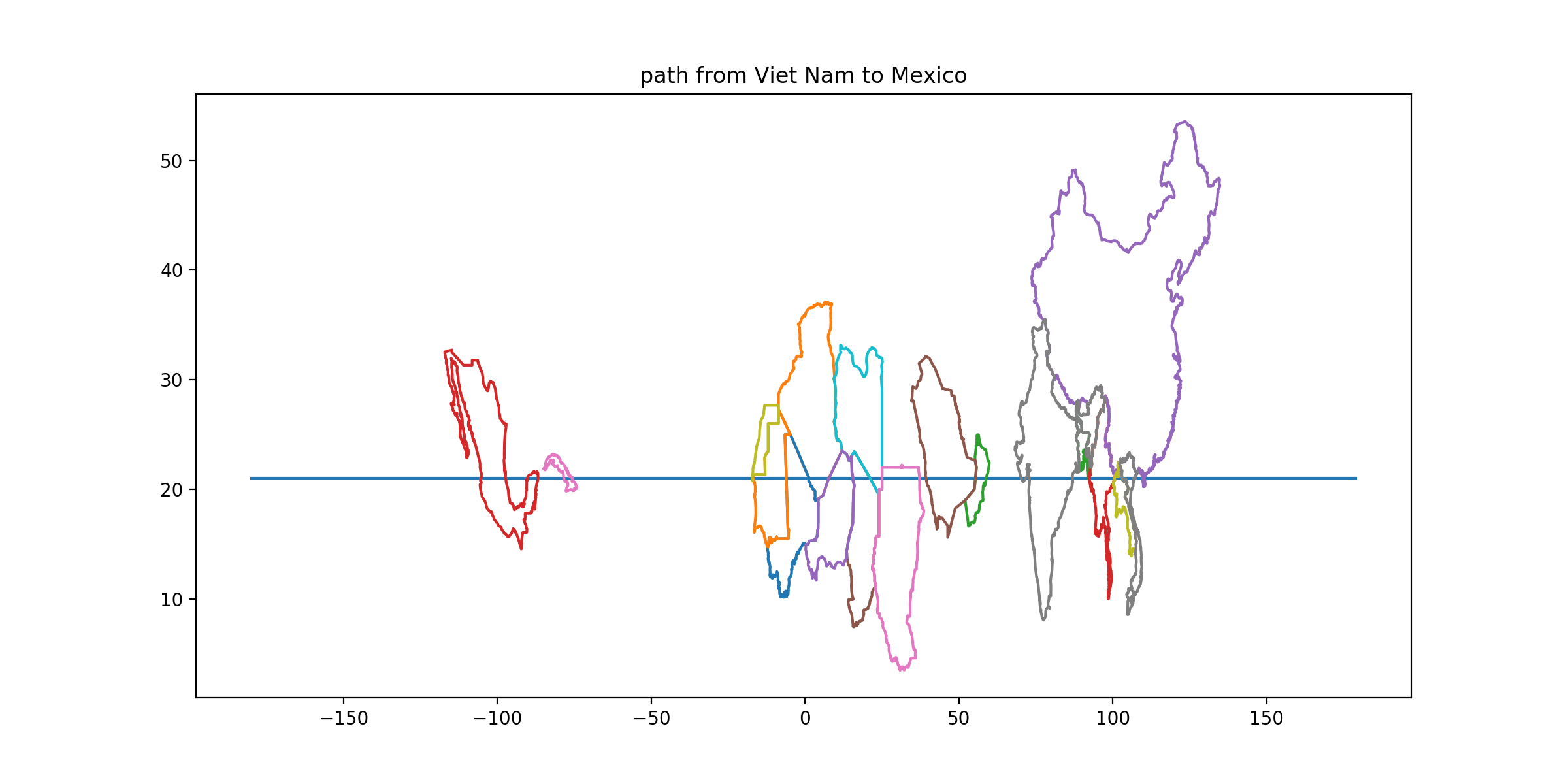
CLUE: From its capital, head east. Stop in the capital territory where the ratio of the longest overland road trip[8] to the longest great circle separation of two points in the same territory is largest.
DESTINATION: Mexico
DESTINATION CAPITAL COORDINATES: [19.43, -99.13]
READOUT LETTER: A from “Ecuador”
SOLUTION: The longest overland road trip in Mexico, by our definition, would begin in Cabo San Lucas run up around the Gulf of California (near Tijuana), around the Veracruz coast to Cancun. The detour around the Gulf makes this much longer than a straight-line great circle from Tijuana to Cancun. Nothing else at this latitude is comparable.
-
CLUE: From its capital, among all the countries with any land territory 6004 km away, stop in the one which has land borders with only one other country (although it and a current non-land-border neighbor have a small sovereignty dispute which might be imagined to add a second land border someday.)
DESTINATION: Canada
DESTINATION CAPITAL COORDINATES: [45.41, -75.7]
READOUT LETTER: P from “Paraguay”
SOLUTION: Canada has only one neighbor. Could it resolve the disputed sovereignty of Hans Island by drawing a border down the middle?

-
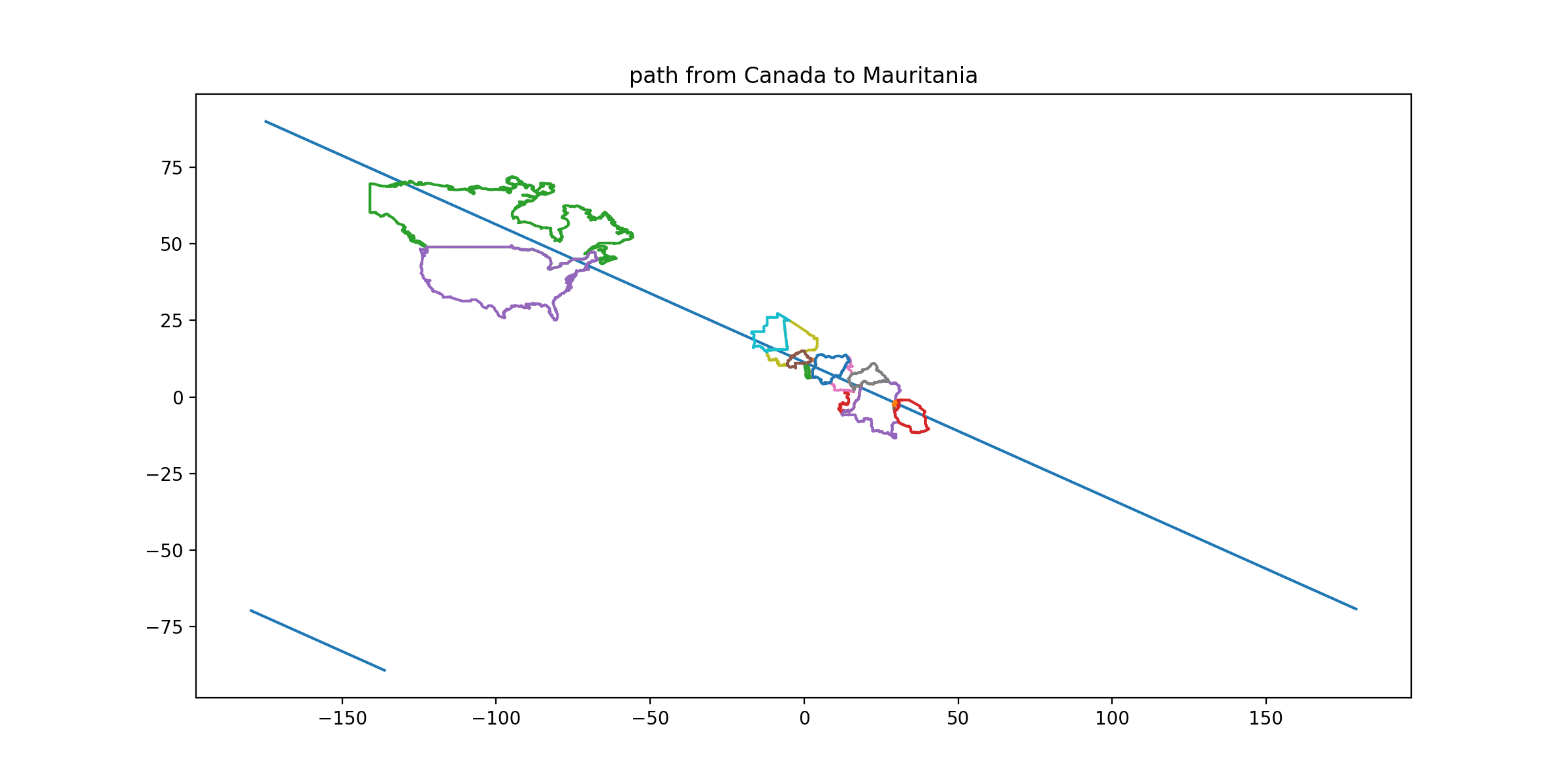
CLUE: From its capital, move along a path that takes you south 0.45 degrees of latitude for every 1 degree east in longitude. Examine the polygonal spaces between the convex hull of, and the actual border of, each contiguous territory. Stop in the country for which this exercise yields the largest perfect triangle[9]. (You should hit this territory with over 100 miles to spare, and miss the country whose protruding corner fills the triangle of interest.)
DESTINATION: Mauritania
DESTINATION CAPITAL COORDINATES: [18.07, -15.97]
READOUT LETTER: O from “Norway”
SOLUTION: Many Saharan countries have numerous straight-line borders defined by survey lines. A square corner of Western Sahara protrudes into Mauritania such that its convex hull adds a triangle. You can quickly inspect sub-Saharan Africa to verify that this is the only candidate for ‘largest triangle’. (Solving hint: The line I describe is straight on an equirectangular (or plate carrée) map. If you can’t find a plate carrée, the best solve method may be to calculate a series of lat/long waypoints and transfer them to another map.)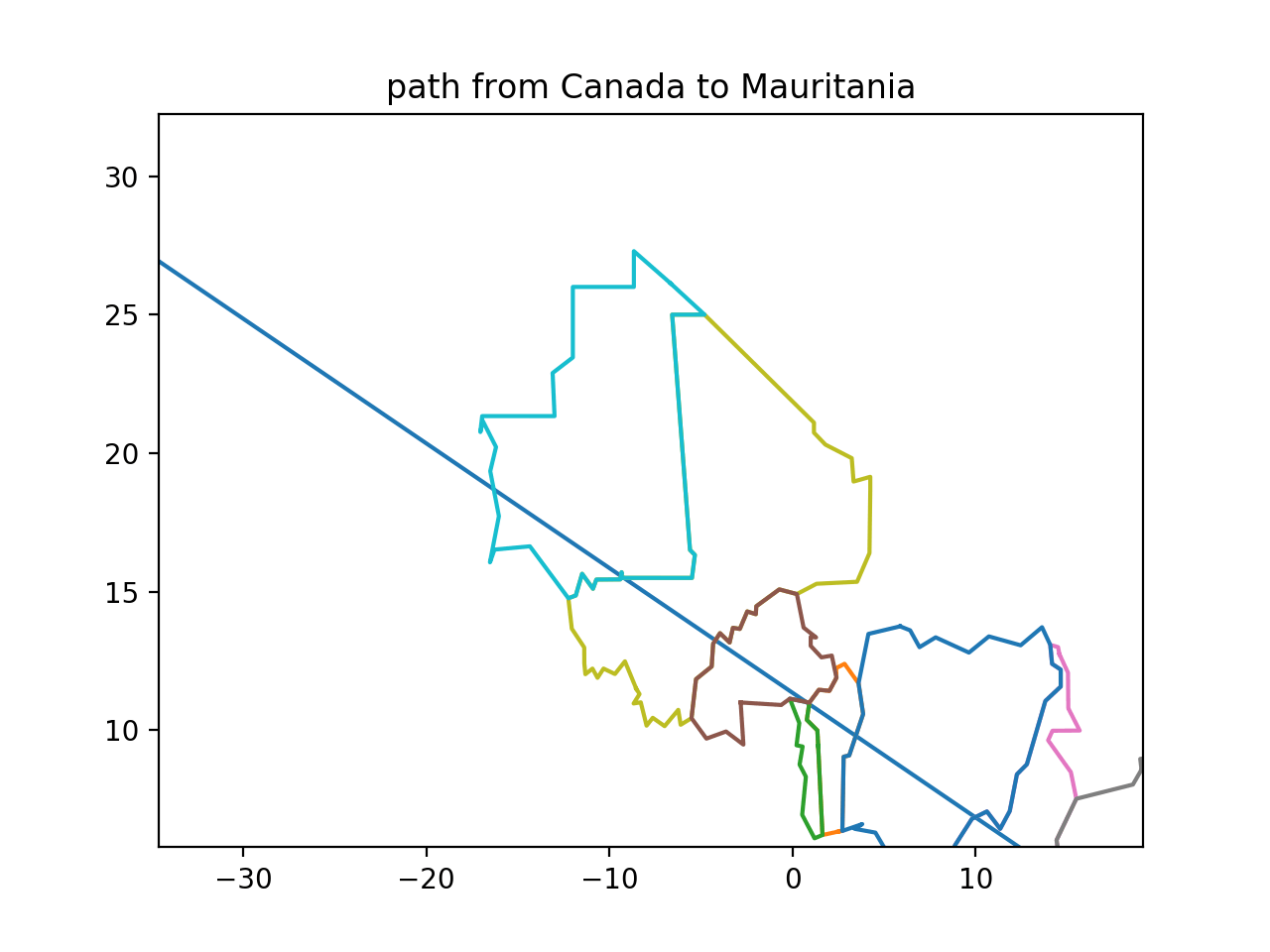
-
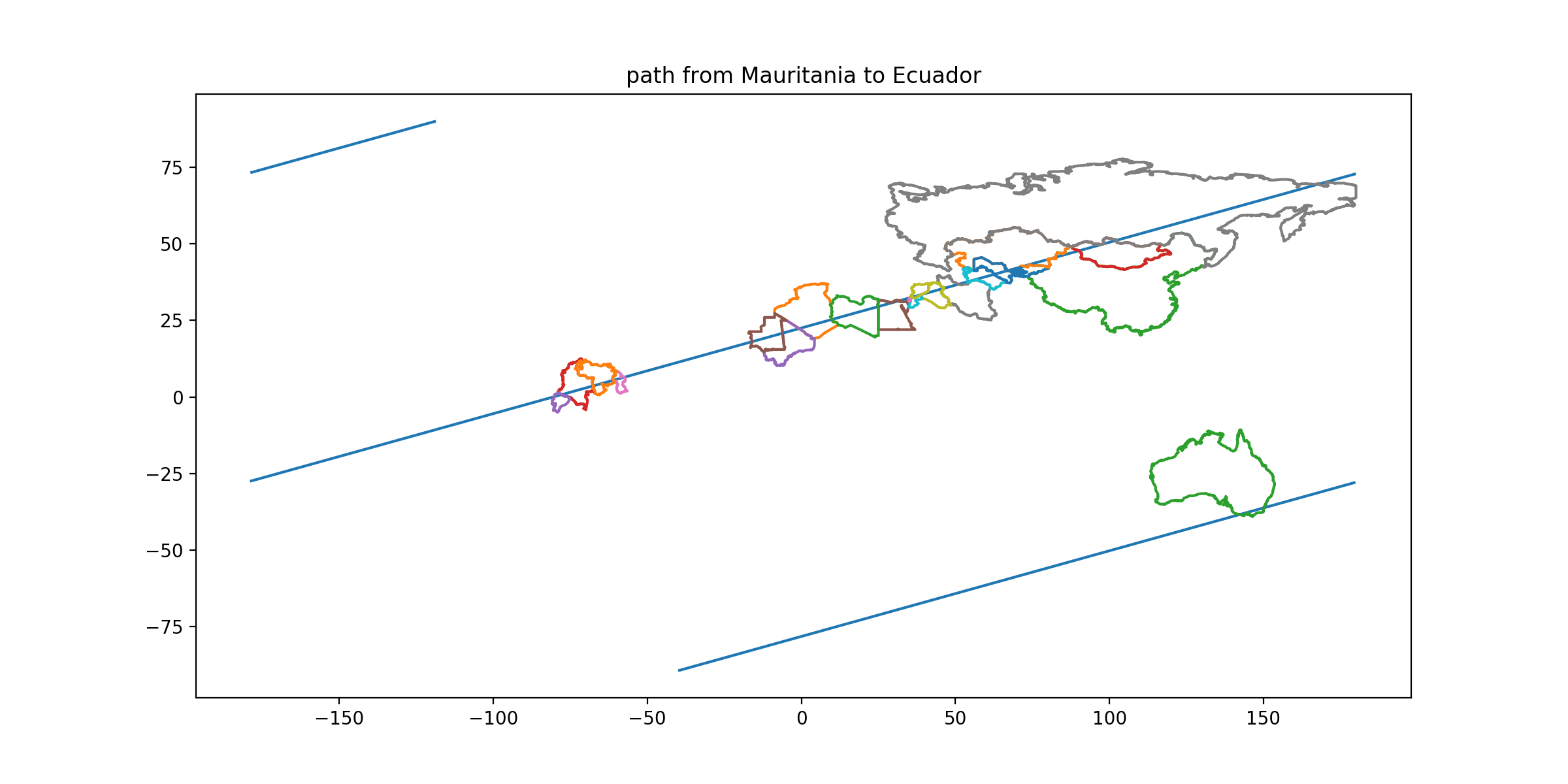
CLUE: From its capital, move along a path that takes you south 0.28 degrees of latitude for every 1 degree west in longitude. Stop in the only capital territory you encounter whose northernmost point is east of its southernmost point. (Both the northern and southern points of your goal are unambiguous. Slightly south of your path is a country whose northernmost point might move east or west of the southernmost depending on small changes in tidal mudflats.)
DESTINATION: Ecuador
DESTINATION CAPITAL COORDINATES: [-0.22, -78.5]
READOUT LETTER: K from “Kenya”
SOLUTION: Ecuador. Guyana, Venezuela, Colombia, and mainland Australia (and Brazil, which your route skims but should not quite cross) have northern extrema west of their southern extrema. The parenthetical hint should warn you to skirt Suriname to its north.
-
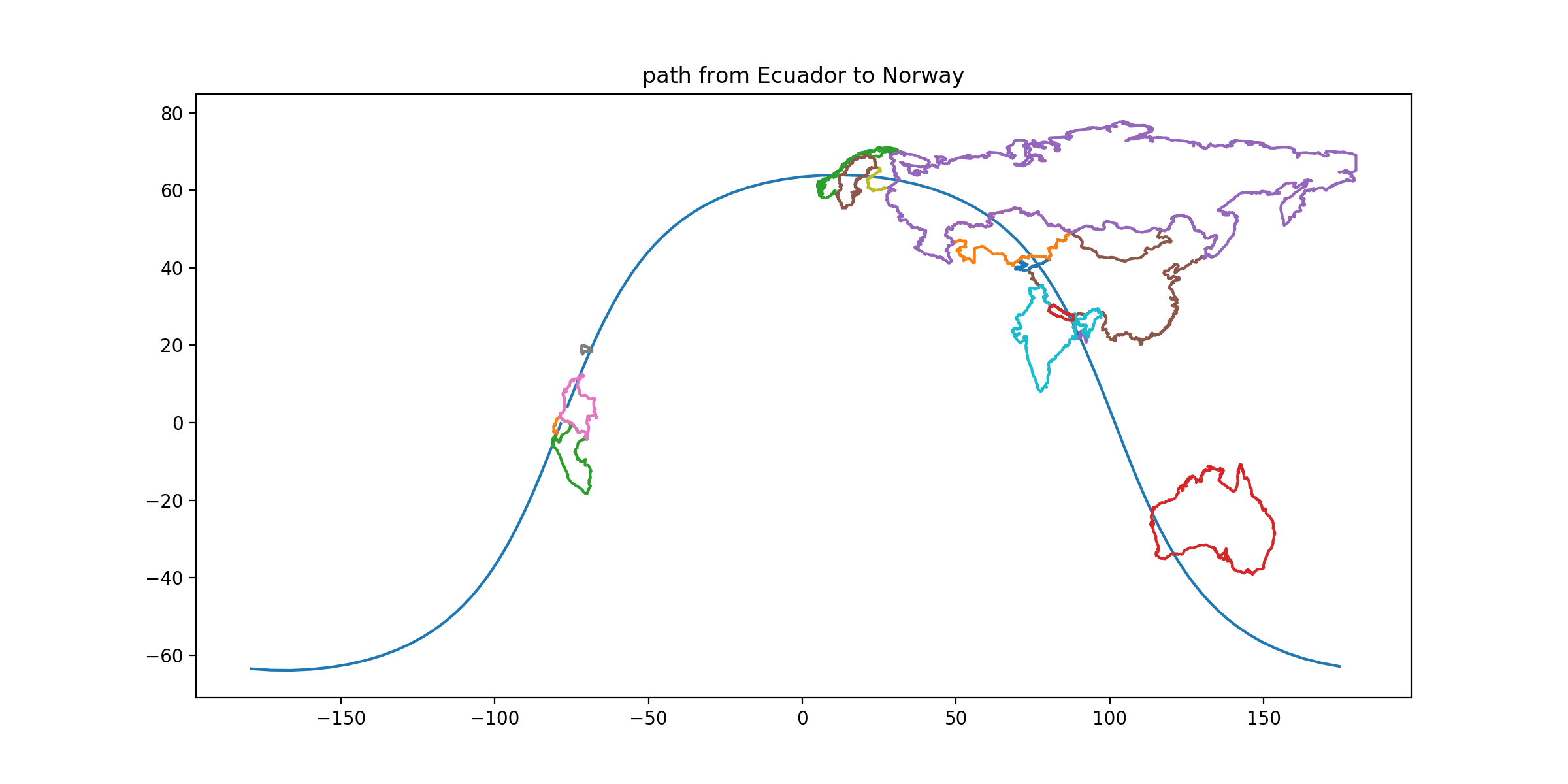
CLUE: From its capital, follow a great circle that also passes through Lake Issyk-Kul. Your destination is the capital territory along this route for which, when you draw the tightest possible circle that contains that territory, the territory’s land area is the smallest fraction (less than 15%) of that circle’s area.
DESTINATION: Norway
DESTINATION CAPITAL COORDINATES: [59.91, 10.75]
READOUT LETTER: A from “Burkina Faso”
SOLUTION: This is, roughly speaking, a measure of how non-circular the country is. For a squat blobby shape it might be hard to draw the tightest enclosing circle, but for a long stick it’s not. For a long skinny shape like Norway’s, you can treat the country’s longest axis as a diameter. A/D² for Norway: 385200/1786² = 0.121 (less than that since “national area” includes many islands). Russia: something like 17000000/8000² = 0.26. (The route passes through Sumatra, which is not Indonesia’s capital territory, but if you evaluated Java carefully A/D² = 138800/1060² = 0.123 and Norway still wins.)
-
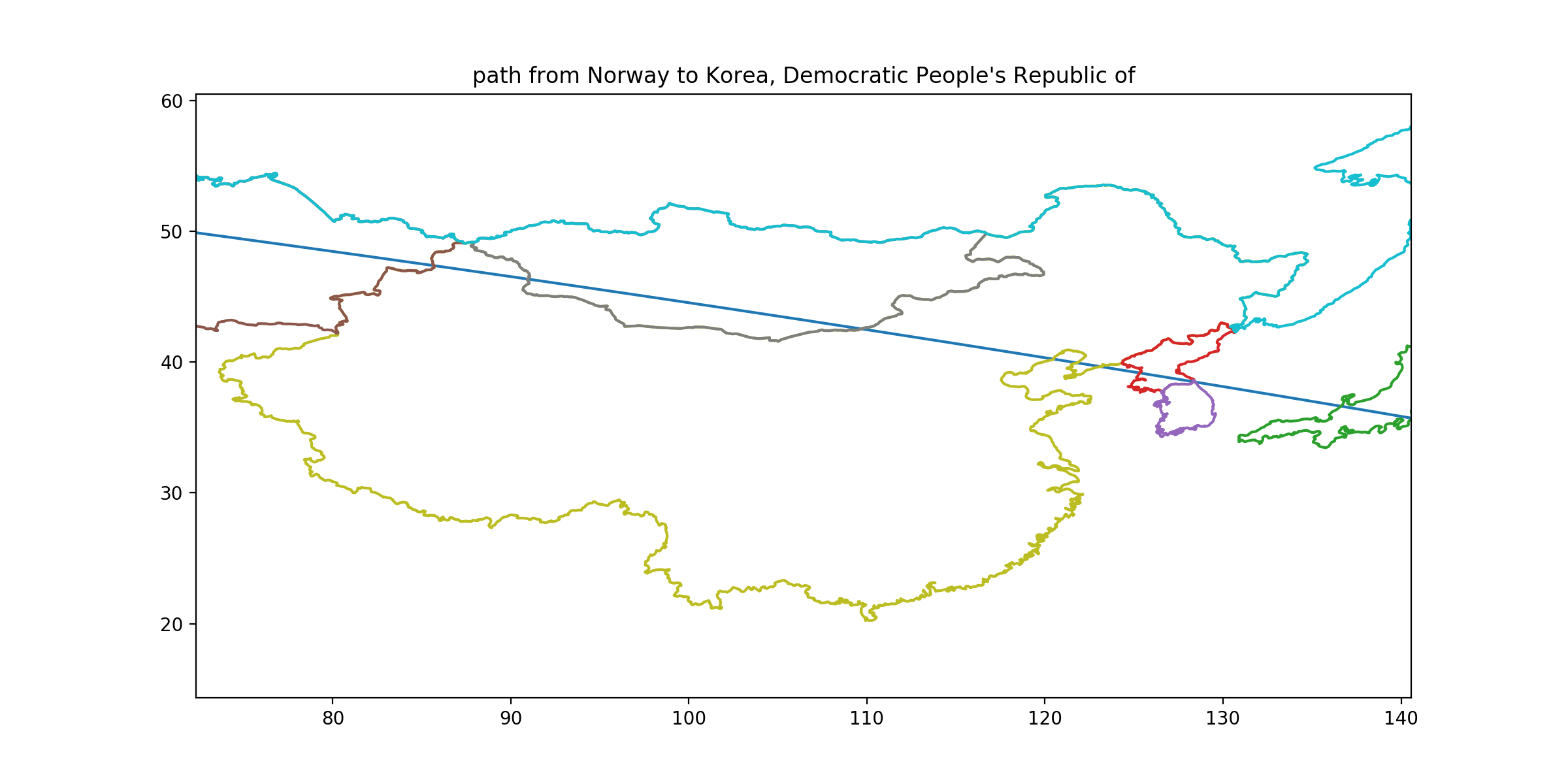
CLUE: From its capital, follow a rhumb line that crosses longitudes at an angle of 15.90 degrees south of east. There is only one capital territory on this path that you will enter by land, exit by land, reenter by land, and exit by sea, in that order. In fact, you should enter and exit it again. (Once you find these conditions, check that you’re on one of the shallowest bearings that allow it. A path erring 1.5° too steep would behave as described but send you astray afterwards.) But don’t stop in that country—continue along this path and visit the very next country you reach.
DESTINATION: North Korea
DESTINATION CAPITAL COORDINATES: [39.02, 125.75]
READOUT LETTER: A from “Canada”
SOLUTION: This path goes Kazakhstan-China, China-Mongolia, Mongolia-China, and China-Bohai Sea. (Depending how accurate your pathfinding is, you may enter and reenter: Estonia, Latvia, Peru, but never with the specified sea/land sequences.) The next country after China on this path is North Korea. The error-check should help ensure that you’ve gone through Liaodong Bay and the Liaodong Peninsula on the way to North Korea, since erring too far south could lead you through Laizhou Bay, the Shangdong Peninsula, and South Korea.
-
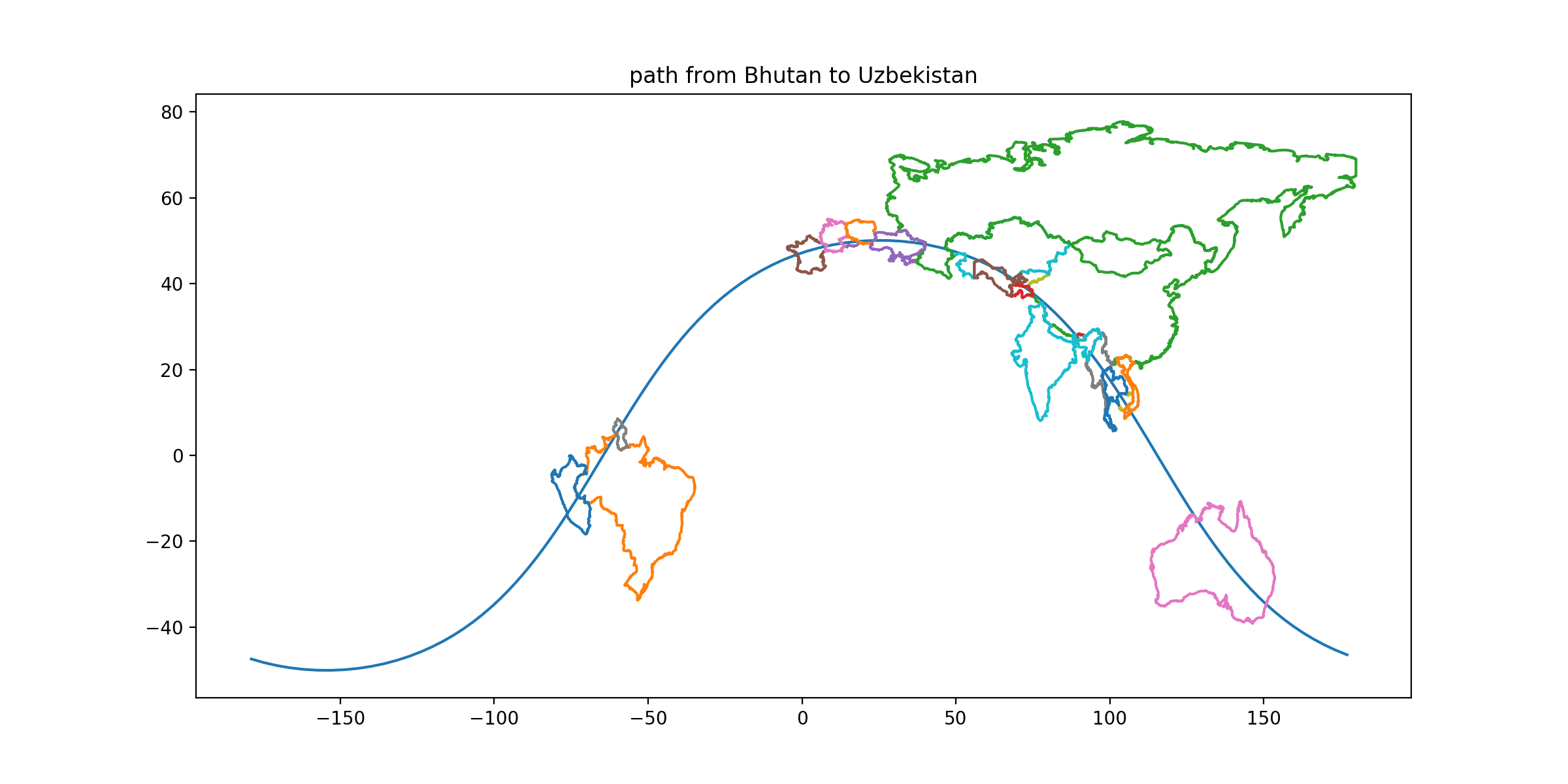
CLUE: Explore the countries with land territory a distance 3586 km from its capital. Stop in the country which lies entirely within (although it’s a close call on one) the convex hulls of TWO different contiguous territories.
DESTINATION: Bhutan
DESTINATION CAPITAL COORDINATES: [27.46, 89.63]
READOUT LETTER: R from “Mauritania”
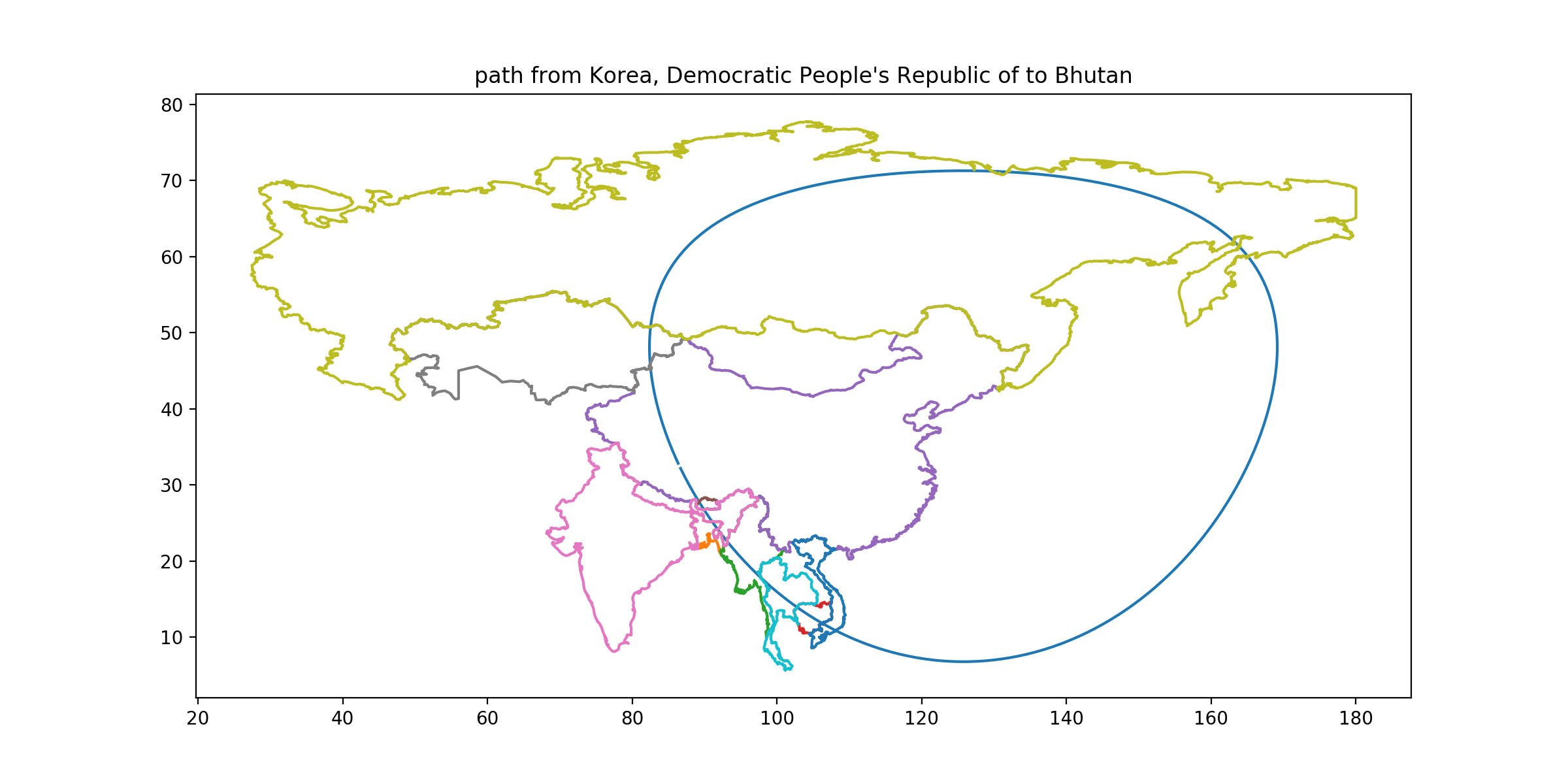
SOLUTION: Bhutan is hugged by arms of both India (say Keylong, HP to Roing, AP) and also China (say Bulang Shanxiang to the Nepalese border by Phulpingkatti). The image below shows that this is true even without any of India's disputed territories. Since Bhutan seems to be the only country with this property: if you have lost the path earlier, you can pick it up here.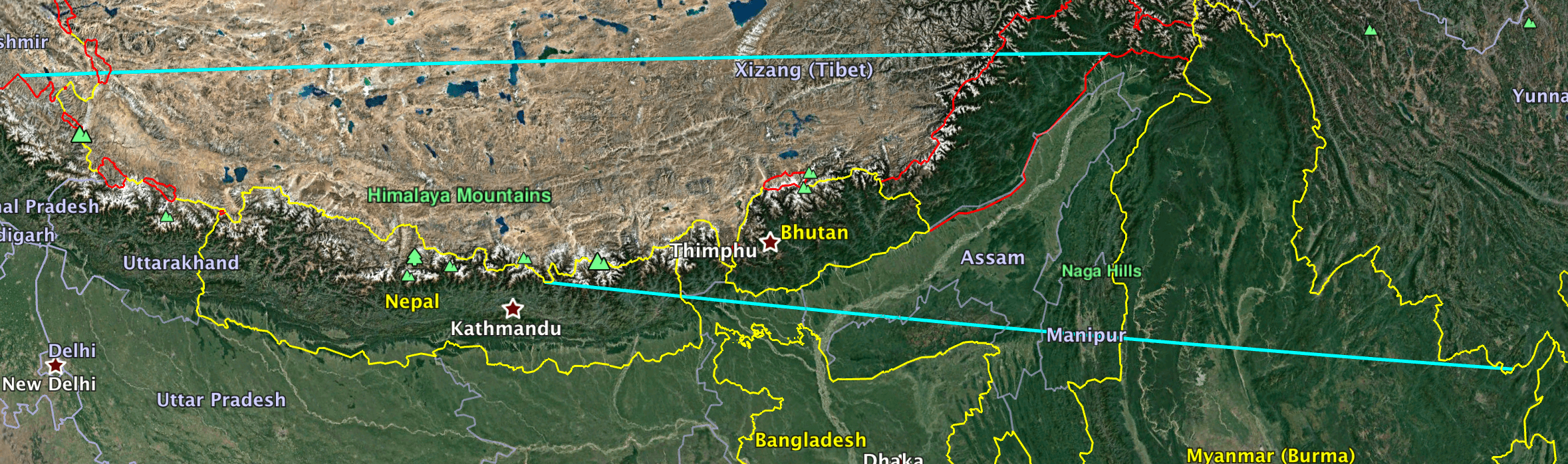
-
CLUE: From its capital, follow a great circle which also passes through the center of Adolphus Island in the Cambridge Gulf. This great circle passes through one exclave; go there.
DESTINATION: Uzbekistan
DESTINATION CAPITAL COORDINATES: [41.32, 69.25]
READOUT LETTER: C from “Mexico”
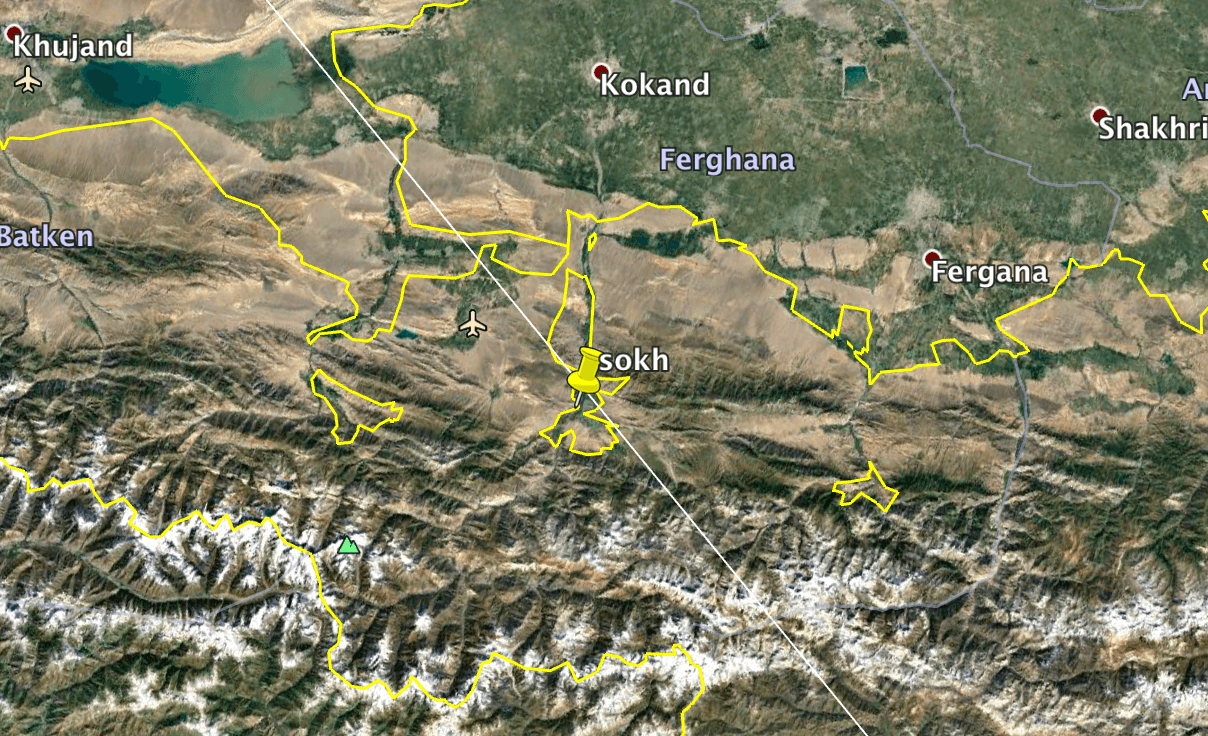
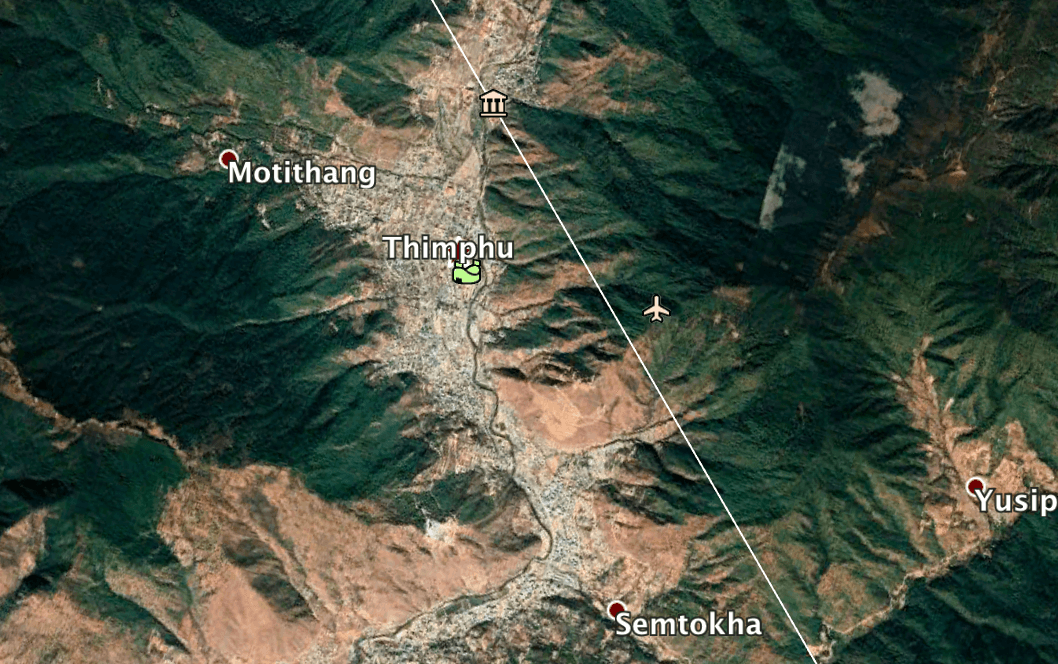
SOLUTION: Welcome to the crazy exclave-encrusted Tajik/Uzbek/Kazakh border. This requires particularly accurate mapping since there are exclaves of multiple countries close to one another—the specification of the CENTER of little Adolphus Island should hint at that. Your path should pass north of Vorukh and south of Sarvan (both Tajik) but cleanly hit Sokh (Uzbekistan). If you’ve hand-mapped your way to this general area and need a software method to disambiguate between the exclaves: guess an exclave, use Google Earth to draw a line to Adolphus Island, then zoom to the middle of the line and see if it indeed passed over Thimpu.
-
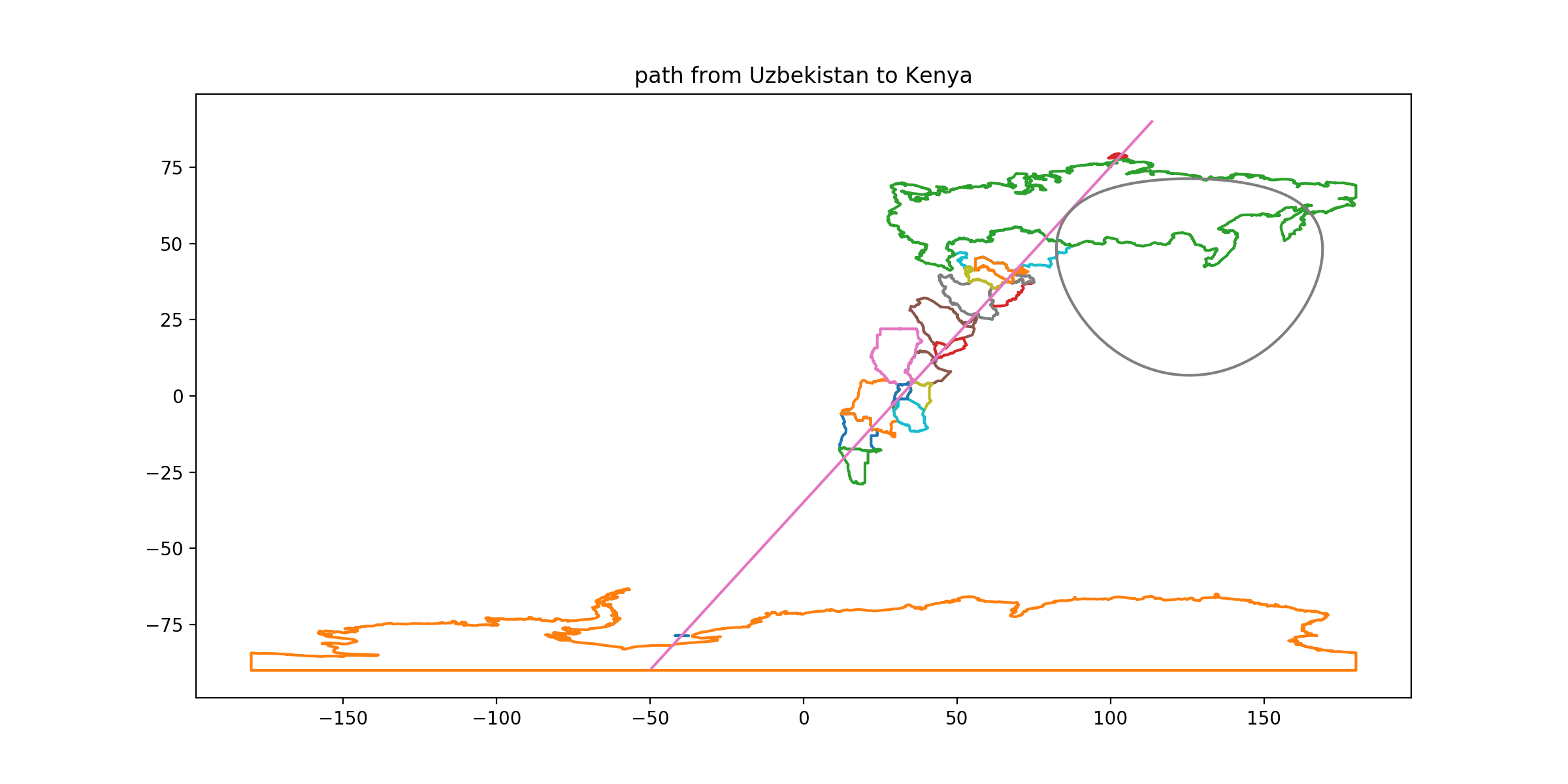
CLUE: On an equirectangular map, draw a straight line through its capital which is tangent to the radius-3586 circle you drew in clue 11. Head southwest, ignoring your starting country and, if necessary, its neighbors. Stop in the first of the three countries on this route—you should hit its northwest corner—which have a relatively long (relative length > 0.2) border along a line of longitude.
DESTINATION: Kenya
DESTINATION CAPITAL COORDINATES: [-1.28, 36.82]
READOUT LETTER: P from “Peru”
SOLUTION: There aren’t many ways to draw a southwesterly rhumb line through Tashkent that hits three straight-bordered countries; the easiest solution may be to guess—with paper and ruler—that you're aiming for some combination of Kenya/Namibia/Angola/Zambia/Botswana and then look back to confirm the tangent condition. In general it’s possible to hit Kenya/Namibia/Angola as a trio, and erring aiming further south will always add a fourth or a fifth. (DRC’s little NS border in the Congo Pedicle, or Uganda’s in Lake Victoria, are shorter than specified.) This should also provide a cross check if you erred on the previous clue; there doesn’t seem to be a three-straight-border path from Dushanbe or Bishkek. Also, there is an enumeration-check in the grid after this clue if you are filling it in as you go.
-
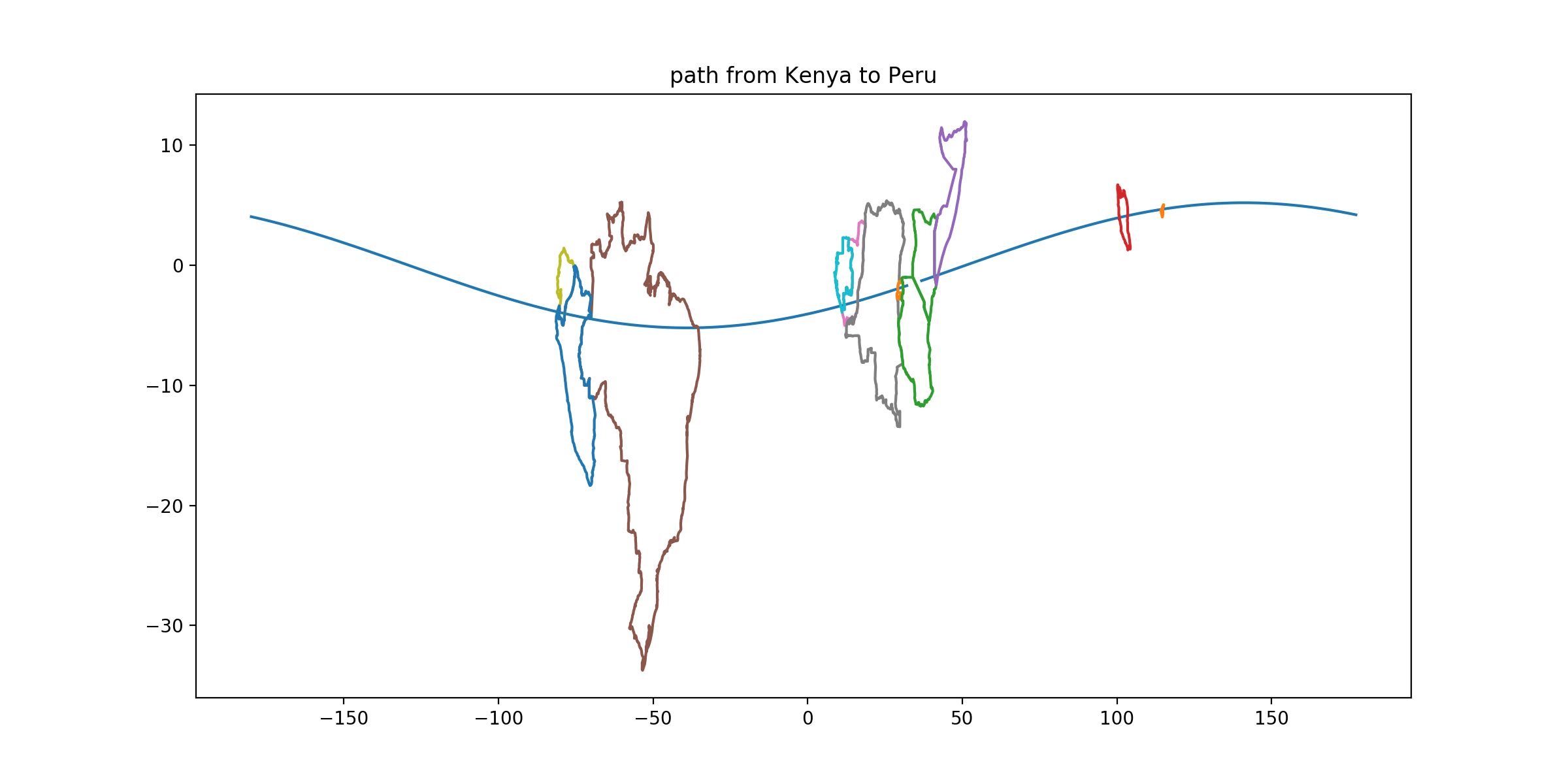
CLUE: From its capital, head west along a great circle with initial heading 264.9°. For each capital territory on this path, construct a quadrilateral whose corners are the southernmost, westernmost, northernmost, and easternmost points of the territory. Restrict your attention to cases where the capital city lies outside, and specifically to the southwest of, this quadrilateral. Go to the country where the quadrilateral has the largest area relative to the capital territory’s area—indeed, you should find that the quadrilateral’s area and the country’s area are nearly equal.
DESTINATION: Peru
DESTINATION CAPITAL COORDINATES: [-12.05, -77.05]
READOUT LETTER: R from “South Africa”
SOLUTION: Your great-circle mapping tool will let you navigate by headings as well as by waypoints. Draw the requested quadrilaterals; for Peru and for Peninsular Malaysia, you will find the capitals cut off as specified. A few countries lack a unique ‘northernmost point’ or whatever, but none in a way that causes ambiguity. Peru’s quadrilateral is large (1.2e6 km^2, almost the area of the whole country) and Peninsular Malaysia’s is a narrow strip, so Peru is your destination.
-
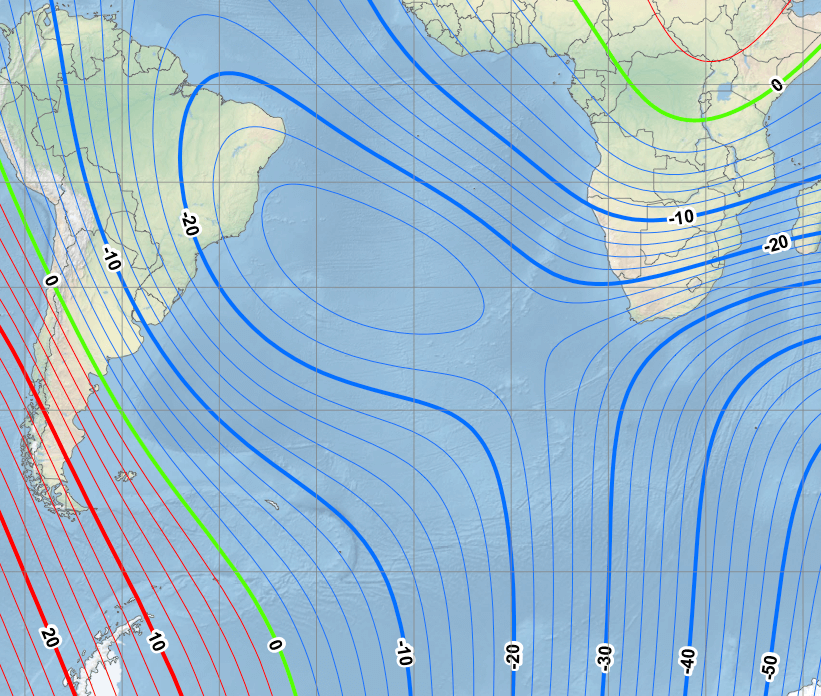
CLUE: In its capital, check the magnetic declination (referencing WMM 2015). Head southeast until you find an isogonic line whose declination is 25 degrees further west. Follow that isogonic line towards the South Magnetic Pole and stop in the first country where you make land.
DESTINATION: South Africa
DESTINATION CAPITAL COORDINATES: [-25.7, 28.22]
READOUT LETTER: O from “Mongolia”
SOLUTION: Look up a magnetic declination map. Lima’s declination is about 1°26m W. Head southeast to find the 26 W isogon—the South Atlantic Anomaly never produces a declination this high, so you can go under it or right through it—and follow the isogon to its only landfall in South Africa, between Cape Town and Port Elizabeth.
-
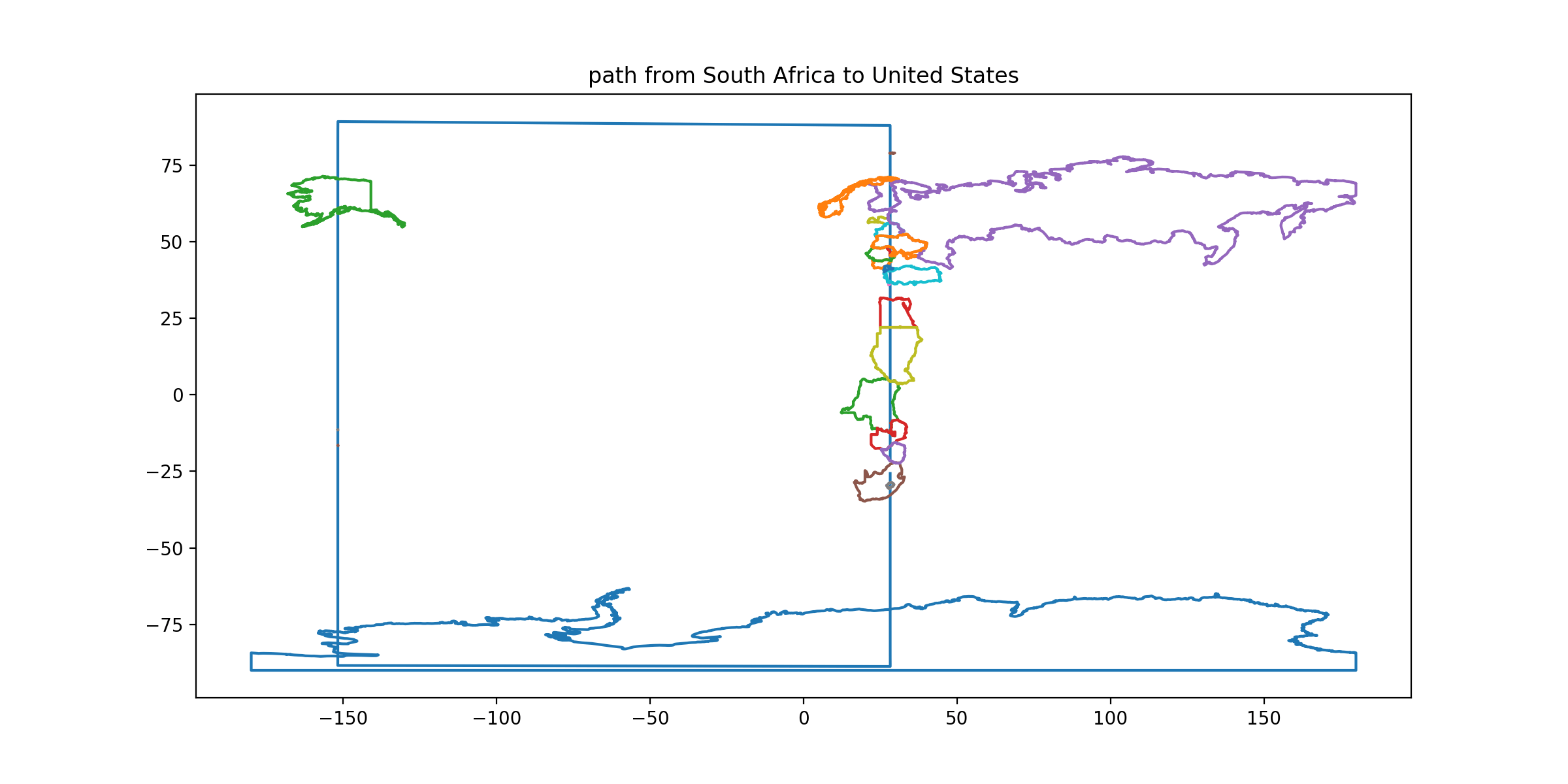
CLUE: From its capital, follow a great circle initially heading due north. This path passes through many countries but usually also passes through at least one land neighbor of each such country. Stop in the first country you enter which has no neighbors along this path.
DESTINATION: United States
DESTINATION CAPITAL COORDINATES: [38.89, -77.0]
READOUT LETTER: V from “Vietnam”
SOLUTION: It’s a close call, but this line does intersect Turkey’s neighbor Bulgaria and (via the line touching Rhodes) Greece. It does, however, go through Alaska without ever touching Canada or Mexico.
-
CLUE: Inscribe a regular tetrahedron in the Earth with this country’s capital as one vertex. Place a second vertex on the west coast of the Antarctic Peninsula. Go to a sovereign nation whose exclusive economic zone, but not its land territory or territorial sea, contains another vertex. (The fourth vertex should be on or near the coast of a country not otherwise referenced in these instructions.)
DESTINATION: Micronesia
DESTINATION CAPITAL COORDINATES: [6.92, 158.15]
READOUT LETTER: I from “Uzbekistan”
SOLUTION: You can sort of construct this tetrahedron by throwing some ruler-and-compass tricks into a great-circle mapping tool, or by doing the solid geometry calculation.
-
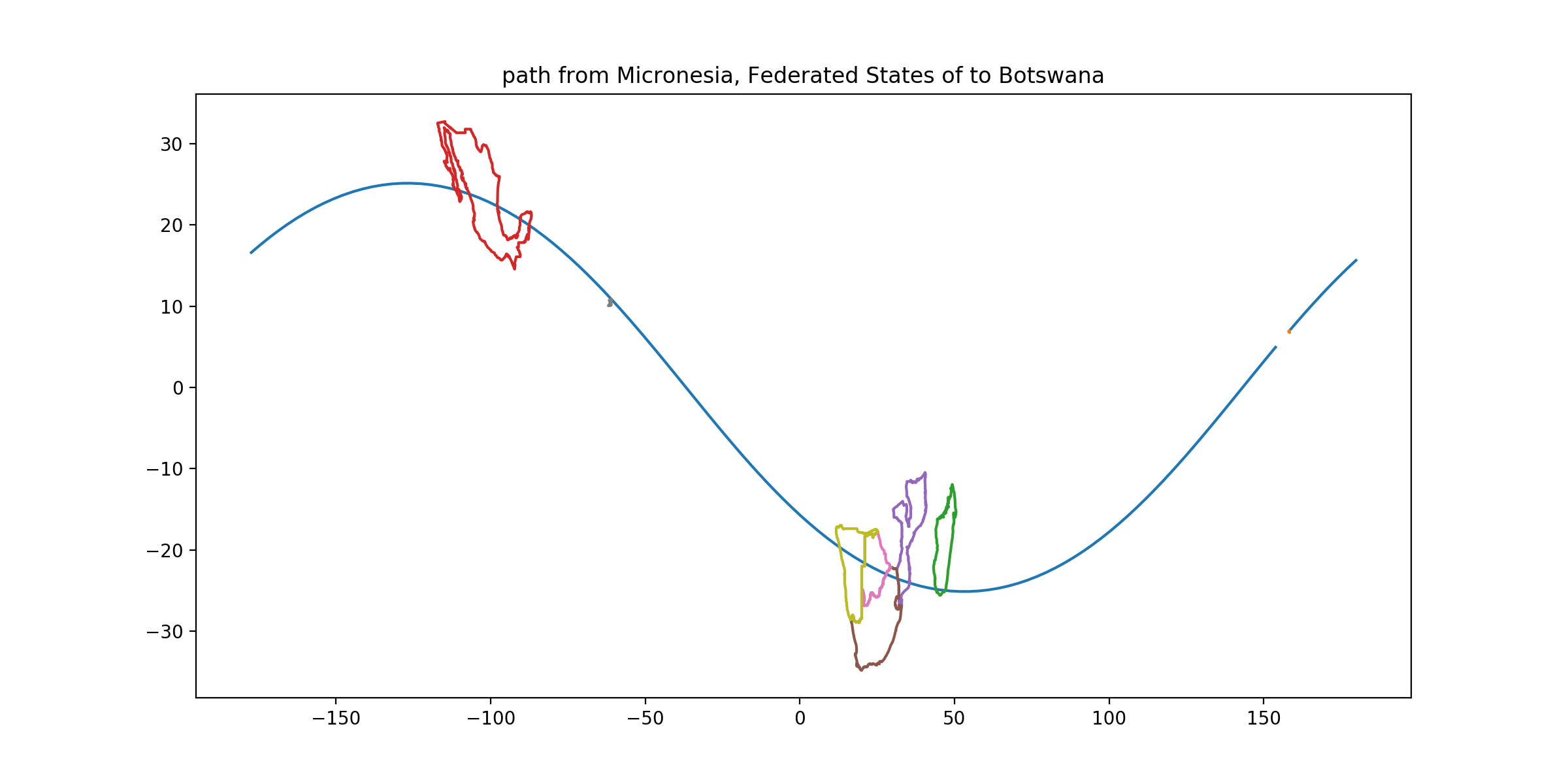
CLUE: From its capital, follow a great circle with initial magnetic heading 240°. Ignoring islands, stop in the capital territory on this route whose land area fills the largest fraction of its smallest circumscribed circle. (Note that the route passes between two countries which are even more circle-filling.)
DESTINATION: Botswana
DESTINATION CAPITAL COORDINATES: [-24.63, 25.9]
READOUT LETTER: N from “Botswana”
SOLUTION: Botswana is really quite circular—but get a load of Zimbabwe and Lesotho. You can get magnetic heading information from online great circle mappers—for example, this link shows the correct great circle as a path from Palikir to a small airport in Botswana. The precise route as specified might clip Trinidad but avoid any circular West Indies islands, but I am not going to make you do this that accurately.
-
CLUE: From its capital, draw a circle of radius 13880 km. (You need four significant figures of that distance.) Look for contiguous territories touching this circle which are fairly long and narrow, with the longer axis more aligned with the arc of the circle and the narrower axis aligned with the radius, such that if the territory’s projection on the radial axis is of length B and its projection on the arc is of length A, then A/B > 3. Among such territories, visit the second-largest one by area.
DESTINATION: Solomon Islands
DESTINATION CAPITAL COORDINATES: [-9.43, 159.95]
READOUT LETTER: C from “Micronesia”
SOLUTION: This distance gets you more than 1/4 of the way around the world, and lots and lots of islands. You’ll skirt the inner edge of Sakhalin (for which A/B > 4) and the outer edge of Malaita (A/B > 3)

-
CLUE: In its capital, you see the International Space Station fly directly overhead. One hour and 56 minutes ago it was over a different country, in principle visible from the capital; go there.
DESTINATION: Mongolia
DESTINATION CAPITAL COORDINATES: [47.91, 106.92]
READOUT LETTER: E from “Indonesia”
SOLUTION: Satellite paths are calculable, of course. You may not want to learn all the details, so here’s a workaround. Since it’s only an orbit and a bit, draw a great circle through Honiara and guesstimate the path incorporating 120 minutes of Earth rotation. You’re looking at Asian countries—maybe China or Russia or Mongolia or Kazakhstan? Maybe Australia? Anyway, they’re big so you do not need the next step to be accurate at the scale of Vatican City or something. For an online-tool-assisted solution, go to a satellite-spotting website, like heavens-above.com. Tell them you’re in Honiara, and ask for a list of ISS overflights. (For extra accuracy, find a nice high-altitude crossing in this list.) For example, in UTC+1 times, on 5 Sep 13:30 the ISS overflew Honiara within 17° of zenith (heading NE), or on 7 Sep it overflew at 1:52 (heading SE). Then make some informed guesses as to where the ISS was 120 minutes (4/3rds orbits) ago, and try to verify the corresponding earlier crossing of that. Where was it at 11:34 on 5 Sep or 23:56 on 6 Sep? Sure enough, Ulaanbaatar had a pretty good overflight at 23:56 on 6 Sep. (Note that if you pick a northbound crossing, two hours ago the ISS was over the Indian Ocean.) Pick a southbound crossing and the preceding country was Mongolia.