 Graphic by Svdmolen.
Graphic by Svdmolen.HYPERBOLOID OF TWO SHEETS
PART 1C: Minkowski's words are in boldface.
 Graphic by Svdmolen.
Graphic by Svdmolen.Minkowski has told us that, for Newton, space and time can be united, but only as a fibre bundle without a unique time-direction. He now begins the investigation which will lead to special relativity: he looks for a "metric structure", in effect a geometry, of four-dimensional space which depends on some parameter, call it c, in such a way that for some limiting case, the time axis loses its uniqueness and the Newtonian fibre-bundle is recovered. If such a parametrised geometry exists, perhaps it, and not the fibre bundle, describes the real world.
"Now what connection has the condition of orthogonality in space with this complete upward freedom of the time axis? To exhibit the connection we take a positive parameter c and consider the locus
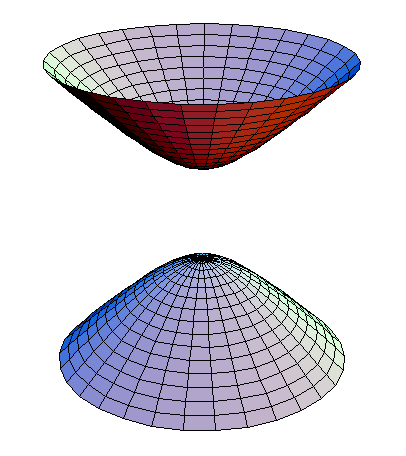
It consists of two sheets separated by t=0 analogous to a hyperboloid of two sheets."
In the graphic above, ct is vertical, and z is not shown.
"Considering the sheet in the region t > 0 we now conceive those homogeneous linear transformations of x, y, z, t into four new variables x′, y′, z′, t′, in which the expression for this sheet of the hyperboloid in the new variables corresponds to the original expression. Evidently the rotations of space about the origin belong to these transformations."
In the figure above, no axes have been drawn, although the vertical t-direction and the the horizontal plane are obvious. One could put x and y axes anywhere in the horizontal plane, and the object depicted would still be a two-sheeted hyperboloid oriented along the vertical axis. Its equation, therefore, according to basic analytic-geometry, must be c² t² - x² - y² = 1. If one were to choose some other pair of right-angled axes x′ and y′, the same would be true, only with primes: c² t² - x′² - y′² = 1. Rotating the space axes leaves the equation of the hyperboloid unchanged.
If one tilts the t-axis away from the vertical, the situation is different: the hyperboloid is leaning relative to the vertical. This lean cannot be eliminated by simply rotating the space axes. However, maybe there is some other kind of transformation, not a rotation, which one can perform on the space-coordinates to get a new system x′, y′, t′ which will formally look the same as the unprimed equation of the hyperboloid.
"We shall next obtain a full understanding of the remaining transformations by considering one in which y and z remain unchanged."
That is, we will consider only the x and t coordinates, so we can draw the figure easily on paper: instead of an hyperboloid or, worse, its four-dimensional generalisation, we can draw a simple hyperbola. We will work here with the figure from the printed version of Minkowski's talk.
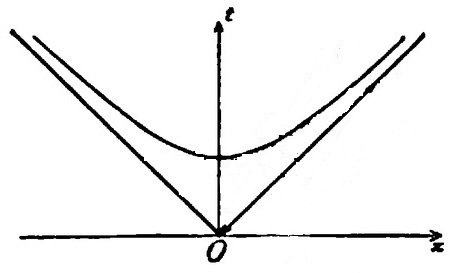
"Let us draw the intersection of this [upper] sheet with the plane of the x- and t-axes, the upper branch of the hyperbola c² t² - x² = 1 with its asymptotes."
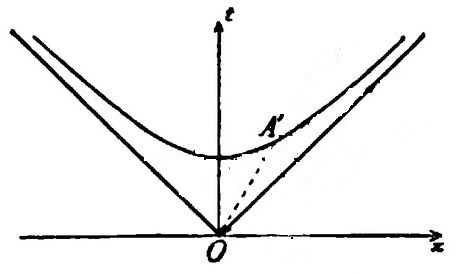
"Then let any radius vector OA′ of this branch of the hyperbola be constructed from the origin O."
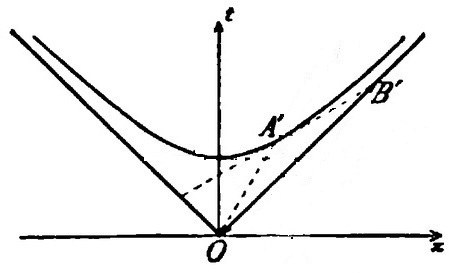
"Let the tangent to the hyperbola at A′ be extended to the right until it intersects the asymptote at B′."
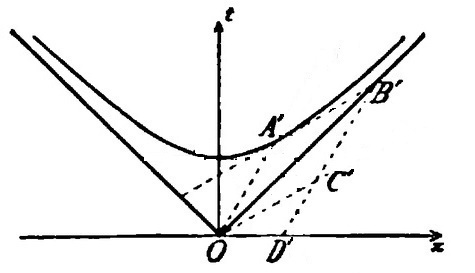
"Let OA′B′ be completed to form the parallelogram OA′B′C′, and finally for later developments let B′C′ be continued to D′, its intersection with the x-axis."
C′ is the intersection of a line through the origin parallel to the tangent A′B′ with a line through B′ parallel to OA′.
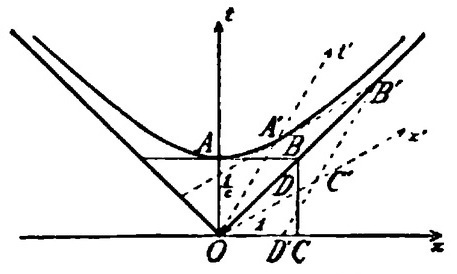
"If we then take OC′ and OA′ as axes for parallel coordinates x′ and t′ with units OC′=1, OA′=1/c, then this branch of the hyperbola again has the equation
and the transition from x, y, z, t to x′, y′, z′, t′ is of the type under consideration."
To which most readers might be forgiven for responding: "Oh is it now?" Minkowski offers no proof; perhaps to him it was obvious. In the next installment, we will fill in the gap. Readers whose algebra is rusty may wish first to review the idea of a unit vector, discussed in the Khan Academy video below.
TIME AND SPACE, by Hermann Minkowski