PART 2B: Minkowski's words are in boldface.

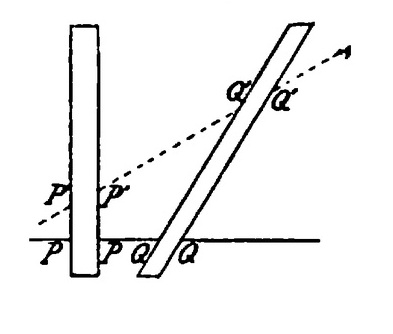
"If, for simplicity's sake we ignore y and z and consider a world of one space-dimension, then parallel strips -- an upright one like the t-axis, and one inclined to it -- represent the path respectively of a stationary and a uniformly moving body which in both cases maintain a constant spatial extent."
What Minkowski means by "constant spatial extent" will be clarified shortly. What matters for now is that the bodies are not changing their shape for any reason unrelated to the Lorentz contraction.
"If OA′ [i. e. the t′ axis] is parallel to the second strip, we can introduce t′ as time and x′ as the space coordinate, and the second body then appears [in the primed coordinate-system] to be at rest, and the first to be in uniform motion.
"We now assume that the first body conceived as at rest has the length l, that is, the cross-section PP of the first strip on the x-axis = l × OC, where OC denotes the unit on the x=axis ; and on the other hand that the second body conceived as at rest has the same length l, that is, the cross-section of the second strip, measured parallel to the x′-axis gives the equation Q′Q′ = l × OC′."
In other words, we are to use the special "primed meters" in which the primed-coordinate unit hyperbola is still a unit hyperbola. It is not clear that Minkowski actually does this in practice. Like most first attempts at anything, the first use of world-lines is hesitant and confused; one regrets that Minkowski does not think of introducing hyperbolic trigonometric-functions and dispensing with the strange units entirely. Later in the talk he will move in this direction, to the great relief of the commentator.
"We now have in these two bodies constructions of two equal Lorentz electrons, one at rest and one in uniform motion."
This is just an aside, relating Minkowski's terminology to Lorentz's. The details of Lorentz's classical model of the atom are unimportant for understanding Minkowski's work; the curious reader may find a clear introductory account here.
"If we keep the original coordinates x, t, fixed, then the section QQ of the respective strip parallel to the x-axis, must be regarded as an extension of the second electron."
The translation of this sentence is difficult; Carus's (given here) does not seem to make sense. Ausdehnung ("extension") could mean "spreading", but the segment QQ is shorter than most others under consideration. It can also mean "extent". Saha translates "Now if we stick to our original coordinates, then the extension of the second electron is given by the cross section QQ of the strip belonging to it measured parallel to the x-axis."
"A simple calculation shows that if (dx/dt) = v for the second strip.
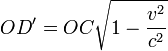
and therefore also

"But this is the meaning of the hypothesis of Lorentz on the contraction of electrons in motion."
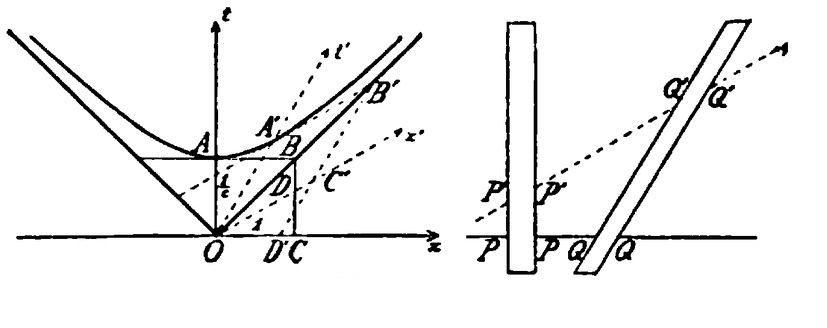
The "simple calculation" which Minkowski omits involves only elementary mathematics, but is still fairly involved. First, recall that the point A′ has (unprimed) coordinates pe + qf, and that the direction of the x′-axis is given by the unit vector
where L² = p² + q².
The point B′ is where a line through A′ in the x′-direction intersects the asymptote ct = x. Let the segment A′B′, which points in the x′ direction and is therefore proportional to e′, have magnitude m. Then
Since OB′ is on the asymptote, the x and ct components must be equal. Therefore
that is, m = L.
Now OC′ has the same magnitude as A′B′ and also lies along the x′-axis. Therefore
It can be seen from the figure that OC′ is the vector sum of OD′ and some vector D′C′ in the ct direction, i.e. parallel to OA′. Let R be the length of OD′, so that OD′ = Re, and let λ be the ratio between the magnitudes of OA′ and D′C′. Then we have:
Equating the components, we find
Solving the two equations simultaneously, we have R = q - p²q. Bring the right side to a common denominator and multiply by 1 in the form q/q to find R = q(1 - (p²/q²))
But p/q (that is, λ) is just the velocity of the second body (divided by c), as Minkowski has already explained, so we can write
This looks promising. To complete the proof, let h be the magnitude of OC. From the figure, when x = h, ct is also h, and the hyperbola is given by c²t² - x² = h². In particular, since A′ is also on the hyperbola, q² - p² = h². Dividing by q² and using v/c = p/q, we find (h/q)² = 1 - (v/c)². Solve this for q² and insert it into the square of the formula for R² we have already obtained. Behold:
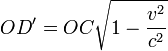
Although I was unaware of it when I wrote the above, I have since learned that Arnold Sommerfeld gives a different proof in the notes to Das Relativitätsprinzip: Eine Sammlung von Abhandlungen [Leipzig: Teubner, 1913; English translation The Principle of Relativity: A Collection of Original Memoirs, Dover reprint, no date]. Sommerfeld's argument uses only trigonometry, and no vectors, so some readers may prefer it. It is available online in German here.
"If, on the other hand, adopting the system of reference x′ t′, we regard the second electron as at rest, then the length of the first will be denoted by the cross section P′P′ of its strip parallel to OC′, and we would find the first electron shortened in exactly the same proportion with reference to the second. For it is according to the figure:
P′P′ : Q′Q′ = OD : OC′ = OD′ : OC = QQ : PP
That is, the Lorentz transformations are symmetric with regard to velocity; we cannot say which of the two strips is "actually" moving.
"Lorentz called the combination t′ of x and t the place-time [Ortszeit] of the uniformly moving electron and used a physical construction of this conception for the better understanding of the contraction hypothesis. But it remained for A. Einstein [Annalen der Physik, XVII, 1905, p. 891; Jahrbuch der Radioaktivität und Electronik, IV, 1907, p. 411] to recognize clearly that the time of one electron was just as good as that of the other, that is, that t and t′ are to be treated alike. Thus time was the first to be discarded as a concept determined uniquely by phenomena."

"Neither Einstein nor Lorentz disturbed the conception of space, perhaps for the reason that in the special transformation where the x′ t′ plane coincides with the x, t plane it is possible to interpret the x-axis of space as remaining fixed in position."
I do not quite understand what Minkowski means by this.
"To loftily ignore the conception of space in similar wise is doubtless due to the boldness of mathematical discipline!"
Once again Minkowski asserts that the abstract mathematician, untrammeled by experiment, is in a better position than the physicist to explore new frontiers. Minkowski's attitude is discussed in Scott Walter's 1999 article Minkowski, Mathematicians, and the Mathematical Theory of Relativity.
"After this further step, which however is indispensable for a true understanding of the group G(c), the expression postulate of relativity for the demand for an invariance in the group G(c), seems to me very weak. Since the postulate comes to mean that phenomena occur only in the four-dimensional world of space and time but the projection into space and time can still be assumed with a certain degree of freedom, I would rather call this proposition the postulate of the absolute world (or for short, world-postulate)."
Indeed, the use of the term "relativity" to describe the new world-view is both a blessing and a curse; many physicists over the next century will regret that some other term, perhaps "theory of general invariance", had not been selected. However, it seems probable that such a name (to say nothing of "theory of the absolute world"!) would have had much less impact on the general public. The false association of "relativity" with moral and social "relativism" will unquestionably be a major factor in the enormous popular fad for all things Einstein in the 1920s, and will help to ensure that "modern physics" joins "modern art", "modern music", and all the other fashionable modernities in the Twentieth Century pantheon. Of course, this association will then tragically backfire when new barbarians trumpet it as evidence that "Jewish science" is part of a nefarious plot to undermine Western values.
In some future blog, I will explore in more detail the nature of "revolutionary" scientific developments in the early 1900s, and the ways in which they represent not a break with tradition, but a natural extension of it. For now I will simply remark that the Nineteenth was a revolutionary century, renewing its life through an organic process of constant upheaval.
Next: What is acceleration in Minkowski's universe?
TIME AND SPACE, by Hermann Minkowski