


2.10.1 Conditional PDF's and IndependenceWhen considering conditioning events and independence, the definitions from the discrete case carry over directly to the continuous case. For instance, given that an experimental outcome is contained in event A (P{A} > 0), the conditional compound pdf for two random variables X and Y is 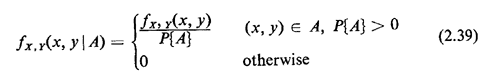
If the event A is stated in terms of the specific experimental value of one of the random variables of the experiment, say Y = 3.23, we have a problem, because P{Y = 3.23} = 0. We circumvent this by considering an infinitesimal strip of width dy in the (X, Y) sample space and equate the conditioning event A to {y  Y Y  y + dy}.
Then, employing the definition of conditional probability for the
conditional event {x y + dy}.
Then, employing the definition of conditional probability for the
conditional event {x  X X  x + dx}, given A, we have x + dx}, given A, we have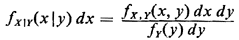
Thus, the conditional pdf for one random variable, given the value of the other, is written 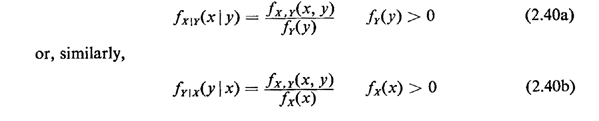
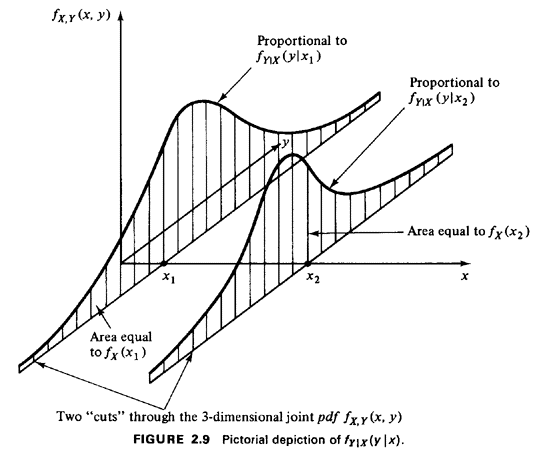
The general shape of this type of point-conditional pdf is determined by a vertical cut through the three-dimensional joint pdf at the fixed value of the conditioning random variable (Figure 2.9). The denominator, which is equal to the area of this cut, is simply a scaling factor. Now, two continuous random variables X and Y are said to be independent if and only if 
Given an arbitrary number N of continuous random variables, they are said to be mutually independent if their joint pdf factors into the product of the corresponding N marginal pdf's. |