


2.4 PROBABILITY MASS FUNCTION
The function px(·) is the probability mass function (pmf) of the (discrete) random varialble X. Clearly, we must have 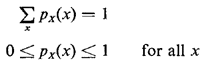
The probability mass function is the assignment of probabilities to each possible value of the random variable. It plays an identically analogous role for random variables that the assignment of probabilities to finest grained outcomes plays in the original sample space. Associated with each pmf is its cumulative distribution function (cdf), which is simply defined to be the probability that the random variable assumes an experimental value less than or equal to a specified amount, 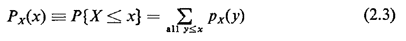
Note that the cdf for a discrete random variable is a step function. It starts at zero for x values less than the smallest possible and proceeds from left to right in steps, the height of a step at X = x0 equaling the probability that X will assume that particular experimental value. The step function eventually reaches unity as a maximum value sincePx( 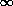 ) = 1 ) = 1
If we wish to obtain information about two or more (discrete) random
variables simultaneously, we must introduce the concept of compound
(or joint) probability mass functions. For instance, for two random
variables X and Y, their compound pmf is given by
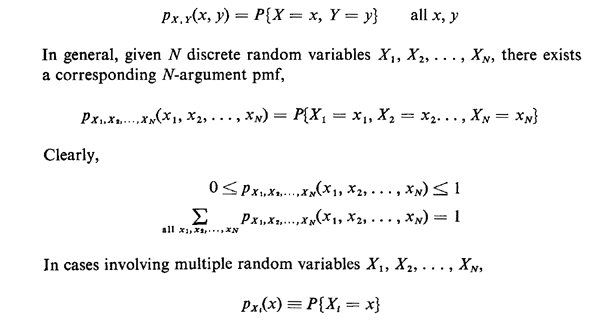
is said to be the marginal pmf for Xi. We can calculate the marginal from the point pmf simply by summing over all the values of the other random variables: 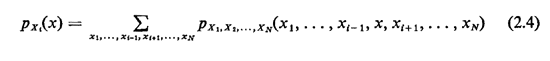
|