


2.8 THE z-TRANSFORMThe expectation of one particular function g(X), namely g(X) = zx, is Of wide use in computations and analysis for those discrete random variables X that take on only nonnegative integer experimental values. This expected value is defined to be the z-transform (or discrete transform or geometric transform or moment-generating function) of px(x), 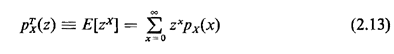
Since 0  px(x) px(x)  1, we are guaranteed that the summation identified
in the definition of pTx(z) will converge for |z| < 1. In fact,
summations associated with z- transforms and their derivatives will usually converge
for larger values of z, but restricting z so that |z| < 1
will assure us of no convergence problems in our work. Here we discuss briefly several
useful properties of
z-transforms. The reader should be aware that material in subsequent
chapters will not emphasize transform techniques and thus all of our
coverage of transforms in this chapter may be considered to be
optional material. 1, we are guaranteed that the summation identified
in the definition of pTx(z) will converge for |z| < 1. In fact,
summations associated with z- transforms and their derivatives will usually converge
for larger values of z, but restricting z so that |z| < 1
will assure us of no convergence problems in our work. Here we discuss briefly several
useful properties of
z-transforms. The reader should be aware that material in subsequent
chapters will not emphasize transform techniques and thus all of our
coverage of transforms in this chapter may be considered to be
optional material.Given the z-transform of a pmf, we can uniquely recover the pmf. We do this by considering the definition of the z-transform, 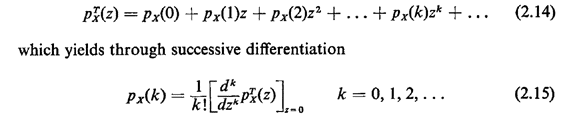
The important moment-generating properties of the z-transform are obtained from the following relationships: 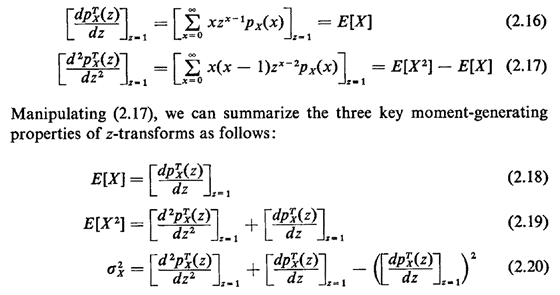
Applications of these relationships are shown in the following section. Exercise 2.10: z-Transform of a Sum Suppose that X1, X2,. . . , Xn. are mutually independent random variables. Let S = X1 + X2 + ...+ Xn . Show that 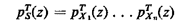
|