


2.9.2 Geometric PMFA random variable X has a geometric pmf if 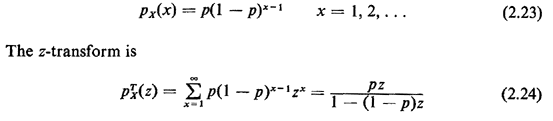
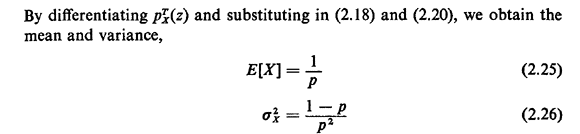
One important interpretation of the geometric pmf involves the "first time until success" in a sequence of Bernoulli experiments (trials). Here "success" corresponds to the Bernoulli random value taking on the value 1. Suppose in the police example above that Yi is the outcome of the Bernoulli trial conducted at the ith hour. Thus, if Yi = 1, the high-crime zone is patrolled during the ith hour; otherwise, it is not patrolled that hour. Suppose that we (as observers) start looking at the high-crime zone during hour 1. We ask the question: Which hour X (X = 1, 2 .... ) will be the first hour during which the high-crime zone will be patrolled? The probability that it will be patrolled during the first hour is simply p. The probability that it will be first patrolled during the second hour is P{ Y1 = 0, Y1 = 1), which by independence is (I - p)p. In general, the probability that it will be first patrolled during the kth hour is P{ Y1 = 0, Y2 = 0, . . . , Yk-1 = 0, Yk = 1}, which by independence is (1 - p)k - 1 p. Thus, the random variable X is a geometrically distributed random variable which, when we substitute p = 0.25, has mean E[X] = 1/0.25 = 4 and variance 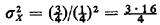 = 12 (and = 12 (and 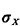 = 2 = 2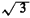
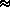 3.44). 3.44).Question: What is the probability that the high-crime zone receives no patrol coverage during any particular 8-hour tour of duty? Exercise 2.11: No Memory Property of Geometric PMF Suppose we have observed that the high-crime area has received no patrol coverage during the first k hours. Show that the probability law for the hour at which patrol first occurs, given this information, is the same as the original pmf, but shifted to the right k units. Thus, the geometric pmf has a no-memory property in the sense that the time (k hours) that we have invested waiting for the first hour of patrol coverage of the high-crime zone has not in any way reduced the mean or variance or any other measure of the remaining time we must wait until the first patrol. |