


3.3.2 Bertrand's ParadoxThe correct solution to a geometrical probability problem often hinges on proper interpretation of the word "random." In Buffon's needle problem this was relatively straightforward; in other settings it is often not so easy.J. Bertrand (1907) offers a good illustration of the potential pitfalls, plus allowing us to demonstrate our proficiency in deriving distributions of functions of random variables [BERT 07]. The problem is as follows:
Determine the probability that a "random chord" of a circle of
unit radius has a length greater than 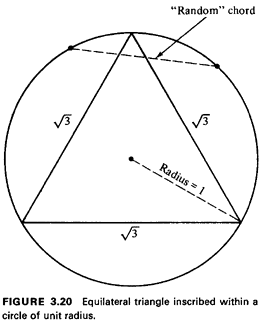
In urban applications, the "chord" may be a street, highway, pipeline, river, railroad, communication link, and so on. The circle may be the locus of points for which a helicopter may travel to in t minutes, or it may be the area of high pollution from a proposed plant, and so on. The threshold criterion that the chord exceed  in length could
refer to adequate coverage of a highway by a helicopter, the
extent of a pollution effect from an industrial plant, and
so on. in length could
refer to adequate coverage of a highway by a helicopter, the
extent of a pollution effect from an industrial plant, and
so on.There are three plausible solutions to this problem. Solution 1: Chord's end points are random. Any chord is uniquely determined by its end points intersecting the circle. These we may assume are uniformly independently distributed over the circumference of the circle. Without loss of generality, we may position ourselves at one of them and examine the relative location of the other. Imagining a vertex of an equilateral inscribed triangle at the conditioning point, the second point must fall on the one-third of the circumference linking the other two vertices. Thus, the probability is 1/3
Solution 2: Distance from the center is random.
The length of any
chord depends on its distance from the center of
the circle and not on its direction. We may therefore assume that
it has a fixed direction perpendicular to a given
diameter of the circle and that its point of intersection with
this diameter has a uniform distribution. For the chord to
have a length greater than
Solution 3: Point of intersection with a perpendicular is random
over the circle. Any chord is uniquely defined by
the location of the intersection of a perpendicular line
extending from it to the circle center. We may suppose that
the location of this intersection is uniformly distributed over
the entire circle. Thus, the probability that this
intersection is within a distance r of the center is
All three solutions are "correct," but each refers to a different
experiment. Recall that an experiment is
characterized by a sample space and its accompanying probability
assignment. The outcome of each experiment can
be described as a value for 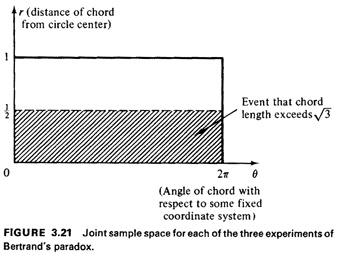
Since the sample spaces (finest-grained list of outcomes) for all three experiments are identical, the probability assignments must differ due to different interpretations of the word "random." Let us reanalyze the three experiments to derive the accompanying probability assignment of each. We seek to find the joint probability density function for E) and R, f.,,,(O, r). For each of the three experiments we can argue that symmetry demands that E) be uniformly distributed between 0 and 2  . Moreover, knowing the value of 0 tells
us nothing about the value of R. Thus, 0 and R must be
independent. The joint density function can then be
expressed as a function of the individual marginal pdf's, . Moreover, knowing the value of 0 tells
us nothing about the value of R. Thus, 0 and R must be
independent. The joint density function can then be
expressed as a function of the individual marginal pdf's,
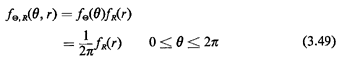
Our task is thus reduced to finding the marginal pdf for R. Solution 1: Chord's end points are random. Without loss of generality we can condition our analysis on a particular point of intersection for one end of the chord, letting the other end be randomly located (Figure 3.22). 
The relative angle between the two intersection points, measured from the circle center, is (  = 2 cos-1 R. By the problem
statement, ( = 2 cos-1 R. By the problem
statement, ( is uniformly distributed between 0 and is uniformly distributed between 0 and
 .
Again by symmetry, we can without
loss of generality condition ( .
Again by symmetry, we can without
loss of generality condition ( to be in the interval
[0, to be in the interval
[0,  ]. We now proceed in the usual stepwise (never-fail) fashion
to find the pdf for R by first finding its cdf: ]. We now proceed in the usual stepwise (never-fail) fashion
to find the pdf for R by first finding its cdf:
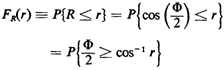
Why was the direction of the inequality changed in the last step? Since 0 is uniformly distributed between 0 and 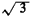 , ,
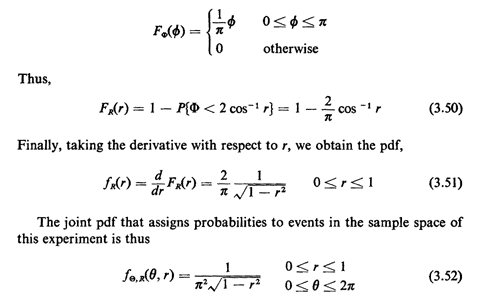
The probability that a "random" chord exceeds 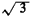 in length is
equal to the integral of f in length is
equal to the integral of f ,R
(O, r) in the joint ,R
(O, r) in the joint  , R
sample space corresponding to R < 1/2 (Figure 3.21). Because of
the angular symmetry of the problem, we see that
this probability is simply equal to the cdf of R evaluated at R =
1/2, , R
sample space corresponding to R < 1/2 (Figure 3.21). Because of
the angular symmetry of the problem, we see that
this probability is simply equal to the cdf of R evaluated at R =
1/2,
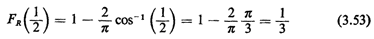
as argued intuitively earlier. Solution 2: Distance from the center is random. In this case, by the problem statement, R is uniformly distributed between 0 and 1. Thus, 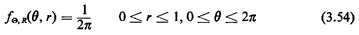
By inspection the probability that a "random" chord exceeds 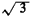 in
length is equal to 1/2.
in
length is equal to 1/2.Solution 3: Point of intersection with a perpendicular is random over the circle. In this situation the "floating end" of the perpendicular whose length is R is uniformly distributed over the circle. Thus, 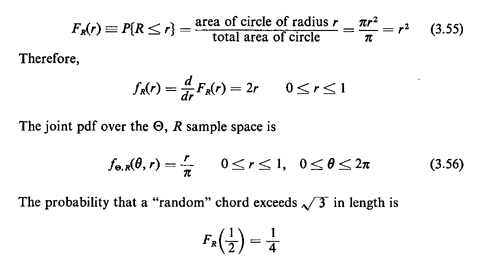
Thus, we see that each solution was "correct," given its underlying probability assignment over the sample space. Geometrical problems that arise in an urban setting can have equally confounding alternative interpretations; thus, the urban analyst must take care to list his or her assumptions explicitly and to question problem statements employing the word "random." |