3.32 Optimal district design in
terms of city blocks
In this problem we shall examine the question of optimal district
design for cases in
which the dimensions of a district can assume only integer values
due to the grid
structure of streets.
Consider again the case described in Problem
3.15, which involved an n
x m rectangular grid district with two-way streets. In
that problem you have
shown that
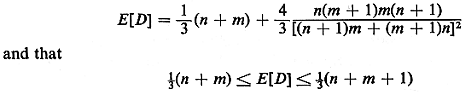
Suppose now that we wish to
design a district so as to
minimize E[D], subject to the constraint that the area of the
district is greater than or
equal to some value A (i.e., mn 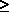 A). (It is not reasonable to set an
equality constraint since m
and n can take only integer values.) For instance, if A = 44, we
wish to find n and m such
that E[D] is minimized and the district contains at least 44 city
blocks. A). (It is not reasonable to set an
equality constraint since m
and n can take only integer values.) For instance, if A = 44, we
wish to find n and m such
that E[D] is minimized and the district contains at least 44 city
blocks.
a. Consider the quantity
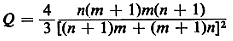
under the constraint n + m = C (where C is a
positive integer constant).
Argue that under this constraint Q is maximized when n = m (if C
is an even number) or n =
m + I (if C is an odd number), and minimized when n = 0 or when m
= 0.
Hint: Q is symmetric in n and m.
b. Show that the following algorithm will give the
optimal district
dimensions [LARS 72a]:
STEP 1: Set i = [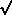 A], where [x] = smallest integer greater
than or equal to x. A], where [x] = smallest integer greater
than or equal to x.
STEP 2: Set j = i - 1 if i(i - 1) 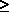 A; otherwise, set j = i. A; otherwise, set j = i.
STEP 3: Set k = i + 1, 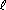 = j - 1. = j - 1.
STEP 4: If kt 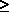 A, set i = k, j = 1; return to Step 3.
Otherwise, stop; the
optimal district dimensions are n = i, A, set i = k, j = 1; return to Step 3.
Otherwise, stop; the
optimal district dimensions are n = i,
m = j.
c. Apply your algorithm to find the optimal
district dimensions for the
case A = 44.
d. Compare numerically E[D] for the cases: m = 7,
n = 7; m = 6, n = 8; m =
5, n = 9; m = 4, n = 11. (All these designs satisfy mn 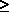 44.) What do you conclude
from these numerical
comparisons? 44.) What do you conclude
from these numerical
comparisons?
|