


6.4.14 Multiroute Chinese Postman ProblemJust as in the case of node covering, multiroute edge-covering problems are very meaningful and applicable in the urban environment. Urban areas are obviously subdivided on a routine basis into smaller districts that can be covered by a single mailman or refuse-collection truck or parking-meter reader or snowplowing truck. This districting aspect is an integral part of the multiroute Chinese postman problem. This problem is usually referred to as the constrained Chinese postman problem (CCPP), since the need to subdivide an area into many routes arises due to some constraint(s), such as the maximum distance that a mailman can cover walking during a normal day or the maximum weight or volume of solid waste that a refuse collection truck can carry or, very often, other limits on some measures of workload that have been agreed on in a labor contract. The CCPP has not been investigated extensively to date, but practical approaches to it--in the context of the delivery of urban services--have been suggested for both undirected [STRI 70] and directed [BELT 74] networks. Because of the relative ease with which the single-tour Chinese postman problem can be solved, the "route first, cluster second" strategy seems to be the favored one in this case: a giant tour is first found and then divided into m subtours, where m is the number of available vehicles. However, with no "best way" available for breaking up the giant tour into shorter subtours, this approach depends to a large extent on the ability and experience of the analyst. In fact, the approach described below for an undirected network [STRI 70] is most effective when carried out manually with the assistance of a good map. The key to the success of the approach is to subdivide the graph G', on which the large, single tour is drawn (see Section 6.4.4) in such a way as not to create odd-degree nodes on the boundaries between subtours. Since G' has been derived by applying a CP algorithm to the original graph G. G' has no odd-degree nodes. Therefore, all the nodes in the interior of subtours will be even-degree nodes and the partitioning process can create odd-degree nodes only on the boundaries between subtours. To avoid this, it is important to draw continuous boundaries for each subtour, so that an even number of edges is incident on each node. The following describes informally a possible heuristic approach: Constrained Chinese Postman "Algorithm" (Algorithm G.9)
Example 14: Tour of the Mailman, Revisited 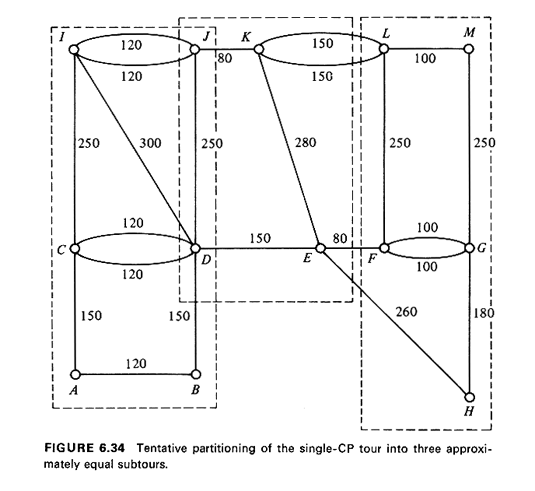
Two disadvantages of the approach that we just illustrated are readily
apparent. First, some trial-and-error work may be required before a set of
feasible tours is obtained. This is due to the fact that the subdivision of
the tour is initially made by inspection alone. Second, the algorithm above
does
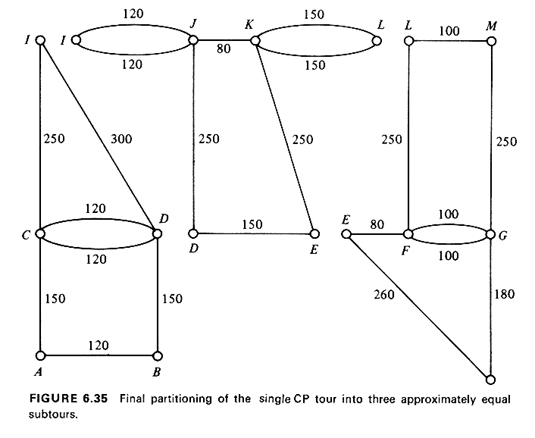
not take into consideration the distances involved in getting to each district from the central station (post office, depot, etc.) and back. These distances--or, better, the time required in practice to cover them--are considered to be second-order-effect quantities. |