Physics

There are two main properties that allow the Levitron to levitate stably. The first is the magnetic repulsion, which provides the force for levitation. The second are gyroscopic effects due to the spinning of the top, which account for the stability of the levitation.

The Levitron consists of a base and a top. The base is a ring magnet with north oriented upwards. The top is a magnet with north oriented downwards. The two norths repel, thereby providing an upwards force on the top due to the magnetic field from the base.  A diagram can be found in Figure 1.

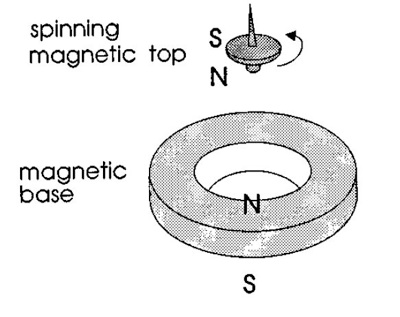
Figure 1: A simplified version of the Levitron.  The base is oriented such that it repels the top.  [1]

In the ideal case, the force on the top due to the magnetic field exactly balances the force due to gravity.  In order for these two vectors to cancel each other out, they need to be equal in magnitude and opposite in direction (compare Figure 2(a) and 2(b)).  The Levitron gives us two parameters to make sure the vectors come close to exactly canceling:  the weight of the top and the leveling of the base.  You can adjust the weight of the top by adding or removing small rubber, plastic, and copper rings, which come with the Levitron.  The legs of the base are adjustable, so that you can make sure it’s level on any surface.

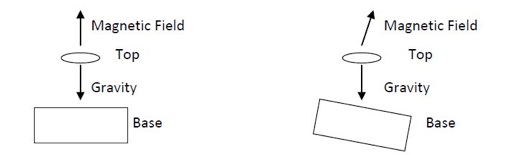
Figure 2(a): Force diagram when Levitron is level, (b): when Levitron is at a tilt.

However, adjusting these two parameters alone are not enough to control stability. There will still be small deviations from the perfectly balanced state. Gyroscopic effects provide this stability. Once the top starts tilting, the forces on it due to both gravity and opposite poles attracting will cause there to be a torque on the top which tries to pull it back down to the base. The angular momentum of the top means that it resists reacting to this torque, and stays mostly upright.  See Figure 3 for a diagram of the torque.

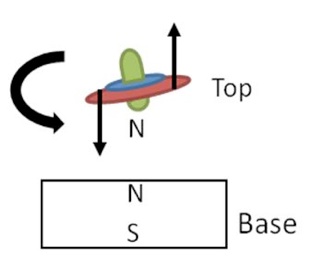
Figure 3: The torque on the top due to the base magnet and gravity.

The other gyroscopic effect that leads to stability is that the top, when it moves off center, will realign to the local magnetic field and precess around it. While it is not intuitively obvious why this helps stability, mathematically, it is the key.  We can find the potential energy of the system by applying the adiabatic theorem to the system, a method we will not go into here. The result is that due to the top’s ability to reorient itself, there is a local potential minimum in the energy of the system. [2]  In other words, if the top wanders small amounts, it will be pushed back down the potential well.  A diagram of the field can be found in Figure 4, and an image of the top precessing can be found in Figure 5.

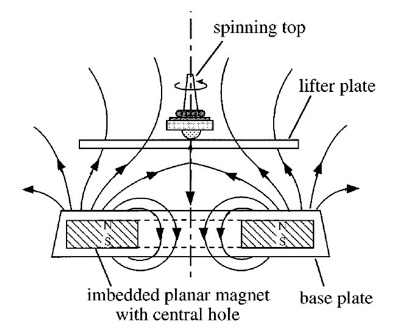
Figure 4: The curve in the magnetic field allows an equilibrium region to form. [3]

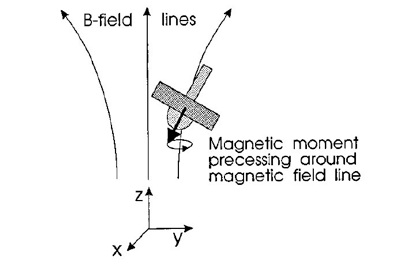
Figure 5: The top reorients itself based on the local magnetic field, and will precess around the local field. [1]

Miscellaneous

There are a few more things worth noting about the Levitron.  The first is that when the magnets heat up, the magnetic field decreases, and the weight on the top needs to be adjusted to account for the change.  Another thing is that when the top starts wobbling too much, the torque on the top will overcome the top’s ability to adjust, so it’s important to keep external disturbances to a minimum.  There are bounds on the rotation rate to ensure stability. When the angular velocity gets too high, the top can no longer reorient itself, and we lose the potential minimum. When it spins too slowly, the top can no longer counter the torque, and it is pulled back down to the plate. This low frequency is called ωcutoff.  In our experiments with the Levitron, we calculated that ωcutoff is around 19.4rps.

References

[1] Simon, Martin D. et al. 1997. “Spin stabilized magnetic levitation.” Am. J. Phys. 65: 286-292.

[2] Berry, M. V. 1996. “The Levitron: An Adiabatic Trap for Spins.” Proc. R. Soc. Lond. A 452: 1207-1220.

[3] Jones, T.B. 1997. “Simple Theory for the Levitron.” J. Appl. Phys. 82: 883-888.

[4] “The Physics of Levitron.” http://www.levitron.com/physics.html.