 Cartesian Coordinates
Cartesian Coordinates
Pre-requisites: N-Tuples.
There are many ways to study and describe geometric objects in
three-dimensional space. One method, pioneered by the Greeks and
formalized by Euclid,
is to study these objects axiomatically: to define points, lines,
planes and other such entities by the axioms they satisfy ("every two
distinct points define a line", for instance).
Another method invented by Descartes
[ Oresme
actually thought of it first, but never gets any credit] reduces
geometry to algebra through the following procedure:
It would be hard to overstate the importance of Cartesian coordinates
in the history (and practice) of mathematics. Previously unsolvable
geometric problems could be converted to long, tedious, but doable
calculations in algebra. [Contrast with the Greek era when even
simple algebraic formulas were converted into cumbersome geometric
figures.] The whole field of trigonometry makes the most sense once
you've introduced Cartesian axes. And, much insight is gained into a
complicated algebraic formula when the formula can be graphed, which
after all is nothing more than drawing all the points with cartesian
coordinates of the form (x, f(x)). Or,
as we will do shortly, of the form
(x, y, f(x, y)).
Exercises:
- Draw a right-handed and a left-handed coordinate axis system. Be
sure to label your axes and to indicate the positive and negative
directions on each one.
- What are the cartesian coordinates of the origin? What can you
say about the cartesian coordinates of a point on the x
axis? Of a point in the y-z plane?
- Draw a coordinate axis system, and then find and label the following
points: (0,6,0), (3,0,-1), (1,2,3).
- Prove the three-dimensional Pythagorean theorem: If a point P has
coordinates
(x1, x2, x3),
then its distance from the origin is
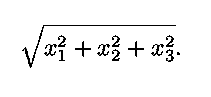
You may assume the normal two-dimensional
Pythagoren theorem.
Solutions to Exercises |
Vector Calculus Index |
World Web Math Categories Page
watko@athena.mit.edu
Last modified November 20, 1998
 Cartesian Coordinates
Cartesian Coordinates Cartesian Coordinates
Cartesian Coordinates