 The Hessian
The Hessian
Prequisites: Matrices, Critical Points
Supposing we have a multi-variable function and that we have figured
out its critical points; it would be nice to have a simple test to
tell whether the critical points are minima, maxima, or saddle points.
We find that, at least for two-variable function, that is functions of
the form z=f(x,y), a fairly simple test does
exist. To introduce this test, we first must define a structure
called the Hessian Matrix.
Developed by
Ludwig Hesse,a German mathematician, the Hessian Matrix
defined for a n-variable function y=
f(x1, x,2,
... xn), is the n by n matrix H whose
(i,j)-th entry is the function of the second-order partial
derivative
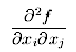 ,
,
a function which can be written in a more compact notation as
fxixj. A
technical point to notice is that the Hessian matrix is not
symmetrical unless the partial drivatives
fxixj are
continuous. For two-variable functions, our Hessian matrix will be a
2 by 2 matrix.
Now, with all our tools in hand, let's state the test of a critical
point of two variable function y=
f(x1,x,2).
The
Second Derivative Test:
If
f(x1,x,2) has continuous (Why is this important?) second
partial derivatives in a neighborhood of a critical point
(a1,a2) definef a number D
by
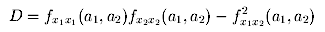 .
.
(Note that this is the determinant of
f's Hessian Matrix.)
Then
(a1,a2) is - a maximum
point if D>0 and
fx1x1<0
- a
minimum point if D>0 and
fx1x1>0
- a
saddle point if D<0.
Further, if D=0, then no conclusion can be drawn, and any of the
behaviors described above can occur. From the above expression for
D, note that if D>0,
fx1x1 and
fx2x2 must have
the same sign.
For an explanation and justification of the above criteria and
expression for D, see Explanation of the
Hessian (a work in progress).
Example:
Let's try this test on a function we've seen before,
f(x,y)=x5+y4-5x-32y,
which has critical points (1,2) and (-1,2). We compute -
fxx(x,y)=20x3
-
fyy(x,y)=12y2
- fxy(x,y)=0
So D(x,y)=240x3y2. (Of course
we quickly note to ourselves that f has continuous second partial derivatives.)
Clearly for the critical point (1,2) D>0 and fxx>0 indicating (1,2) is a minimum point. On the other hand, for the critical point (-1,2) D<0 indicating (-1,2) is a saddle point. This matches our previous conclusion.
N-Variable Functions with N>2
A natural question to ask is whether this second derivative test for two variable functions is easily generalized to higher variable functions. And the answer is "No...well, not easily anyway." Actually the two variable case is a specific case of a more general theorem, but that theorem requires a knowledge of linear algebra to understand. To see it written out, check out pp. 311 of T. M. Apostol, Calculus (John Wiley & Sons, Inc., 1969).
Exercises:
Vector Calculus Index |
World Web Math Main Page
thing@athena.mit.edu
Last modified 18 July 1997
 The Hessian
The Hessian The Hessian
The Hessian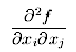 ,
,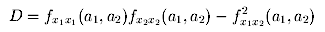 .
.