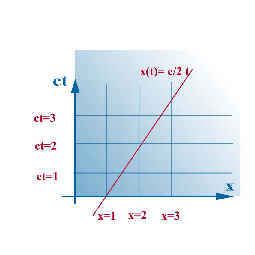
x-t 图的观念相信大家都很熟悉,(fig .1)如果鸟蛋哥哥看到一个子弹以c/2的速度远离他飞走(c是光速),而且每隔一小段时间就把子弹的位置记录下来,那麽在x-t图中所有数据点就会连成图中的线(我把时间的尺度定为c*1 sec/格)
趣 味 问 题 解 答 :
一天,鸟蛋兄弟为了力学作业发生争吵,决定以暴力解决问题。为了公平起见,两人拿一样长的长茅(Lo)决斗,由远处以接近光速的相对速度(v)冲向对方。
由於相对论效应,在哥哥(白色)看来,弟弟的矛比较短Lo'=(1-v2/c2) 1/2Lo,
於是在弟弟还没有刺到哥哥以前,哥哥就把弟弟刺死了。 (图1)鸟蛋弟被解决以後,弟弟的长矛仍然依惯性向哥哥冲来,哥哥闪躲开来。
获得胜利後的鸟蛋这时想到一个问题,依据相对性原理,弟弟也应该看到哥哥的长矛是缩短的(否则就不是"相对"的了),那在弟弟看来,到底发生了什麽事呢?(弟弟看来,自己是怎麽被刺死的呢?)
答案:(真抱歉, 似乎有点难懂, 请大家耐心看看罗)

x-t 图的观念相信大家都很熟悉,(fig .1)如果鸟蛋哥哥看到一个子弹以c/2的速度远离他飞走(c是光速),而且每隔一小段时间就把子弹的位置记录下来,那麽在x-t图中所有数据点就会连成图中的线(我把时间的尺度定为c*1 sec/格)
根据Lorentz tansformation(这个部分大家可以参考别的网站)
在考虑相对论的效应下
鸟蛋弟弟看到在位置x',时间t'发生的事件,若是由鸟蛋哥哥来看,发生於位置=x的地方,时间=t的时候,那麽:
x' =( x - vt)/(1-v2/c2) 1/2
t' = ( t - v/c * x)/(1-v2/c2) 1/2
(v是他们之间相对的速度)
上面这两个方程式是什麽意思呢?假想鸟蛋哥哥(和弟弟相对速度4c/5)看到x=1m,t=7/5sec的时候有一个气球爆炸,那麽他可以用上面的方程式算出弟弟应该在什麽时候、什麽地方看到同一个气球爆炸(只要代进去就好)
t'=(7/5-4/5*1)/ (1-42/52) 1/2 =(3/5)*(5/3)=1(sec)
在鸟蛋问题里,鸟蛋弟弟的速度是-v0,所以上面式子里的v要用-v0代
(注意!这两个方程式是用在t=0时两个人的原点重合,在鸟蛋问题里,你可以设在t=0的时候,两个人头碰头撞在一起,往回推算弟弟和哥哥看来,什麽时後他们戳到对方,你会发现,在弟弟看来,是哥哥先逃过矛,然後以歪斜的姿势刺到弟弟)
如果大家还是觉得一头雾水,那麽这个问题还有别的解释方法
如果大家仔细观察这两个方程式
x' =( x - vt)/(1-v2/c2) 1/2
t' = ( t - v/c * x)/(1-v2/c2) 1/2
令t' =0,
t'= ( t - v/c * x)/(1-v2/c2) 1/2=0,
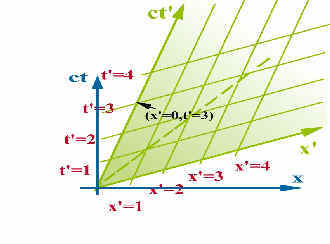
t=v/c *x ,在哥哥的座标系里这是一条直线(fig.2),在这一条线上弟弟看来t'都等於0,同样的,我们可以令t'=1,2,3,4...还有x'=0,1,2,3...,(如图) 我们发现弟弟座标的格线在哥哥看来竟然是歪的,我们举个例子大家可能会比较清楚:
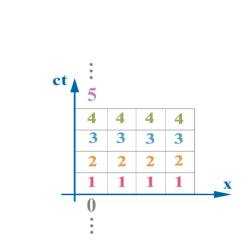
假设哥哥买了4个定时翻面的广告招牌(大家应该都看过这种招牌吧,有一阵子很流行的,像百叶窗一样,定时会转动),每隔一秒就翻面,t= -1~0sec四个招牌上面同时显示0(fig.3),t=0翻面,t=0~1sec上面显示1,以此类推2,3,4...,那麽由相对於哥哥在跑的弟弟看来是什麽样子呢?
在哥哥的时空x-t图里,我们把招牌放上去(fig.4)
然後再把弟弟看来t'=0,1,2,3...sec,x'=0,1,2,3...m的等时,等位置线放进去(在弟弟看来这些线上的事件都是等时,或是等位置的)
(我们之前已经用lorentz transformation导过,所以我就直接放上去了)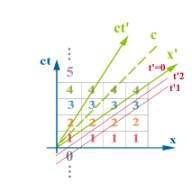
对弟弟来说,从左到右招牌为0,1,2,3对应到t'=t'1的时候,所以弟弟这时候看到的应该像下图最下面的样子
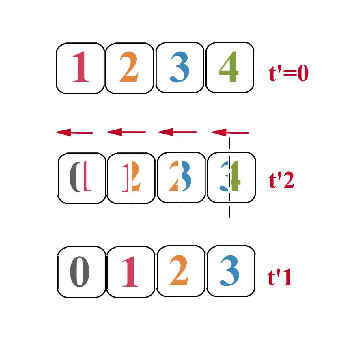
同理,t'=t'2,0的时後,看到的就像上面两个喽!
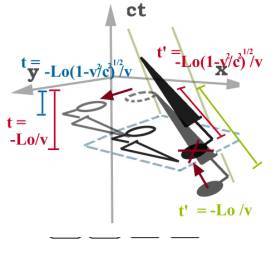
至於鸟蛋问题也同样可以用space-time diagram图解(我画的是x,y,t都考虑进去,实际上只考虑x,t就可以了)
仔细算算看,就会知道在弟弟看来是哥哥先逃跑(要刺到的那一瞬间),但是矛的尖端还留在指着自己的地方,下一秒自己就撞上去了。
这就是鸟蛋paradox的解答
注:我原先出的题目是考虑大家对相对论都有大略初步的了解,解释不够详细的地方敬请见谅,已经有初步认识的人应该看起来不会那麽难懂才对