重力子的自旋之谜

台大物理系 Listeve

        当我们成功的利用量子场论来描述电磁场(QED), 电弱作用(GSW), 以及强作用之後, 我们发现在这个世界上, 只剩下重力这个特立独行的家伙, 还没加入量子场论的行列, 因此我们很直觉的就会开始期待, 哪一天能够将重力理论并入量子场论中, 以相同的语言来描述这些作用力, 物理学家这样梦想着.

 

而在这之前, 我们必须要探讨媒介这个作用力的粒子的性质, 而我们将这个媒介重力的粒子叫做重力子(graviton), 以下就是我利用老师所给的一些资料, 以及许多半调子一知半解的知识, 来做的讨论.

 

一. 讨论spin 0 scalar field是否有机会描述重粒子:

 

 

1. 利用纯量场来描述重力的近似理论-牛顿的万有引力理论:

在Norbert Straumann的文章中, 谈到一开始最直接的想法, 就是以纯量场来描述.

首先由爱因斯坦的方程式与电磁学作类比:

由相对论, 我们知道必须满足以下条件:

□

　

定义 Lagrangian: (space like)

weak field:

 其中

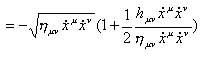
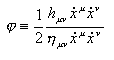
当速度很慢的时候, 可以得到

 

因此我们知道’上面的假设可以导致行星的椭圆运动.

看起来使用纯量场来描述重粒子似乎有些希望.

 

2. 接下来使用Lagrangian density来描述纯量场理论:

 

 (scalar field lagrangian density)

接下来Norbert Straumann可以算出energy-momentum tensor, 虽然我不知道是发生什麽事情:

 

由这个Tensor我们可以算出Total energy

  其中

 

因为 à

 

因此代入Energy的式子中我们可以得到

得到一个”相吸”的结果.

 

文字方块: 以上两个推导结果看起来十分不错, 不过使用纯量场来描述重力作用有一个很大的问题, 那就是纯量场的描述方式真的很”古典” . 因为由上面的结果看得出来, 我们会预测光不会因为重力而偏折.

 

Norbert Straumann提到电磁场的Energy-Momentum tensor会是零, 因此代入上面所推导出来的式子会发现E=0, 因此重力场不会对光子产生作用. 但是天文学家的观测告诉我们, 在1913年的日食观测中发现, 光子的确有受到太阳的重力场而产生偏折的现象(重力透镜), 因此纯量场会造成这个与实验不符合的结果.

       

        在Ray D’inverno的课本中, 告诉我们Maxwell energy-momentum tensor的形式是这样的:

                        à

 

至少可以直接看出来, 在只有gaa不为零的情况下, Tr T为零. 在Malcolm Ludvigsen的课本中也提到, 没有质量的粒子其Tab的Trace为零.

 

另外一个严重的问题, 是发生在移动中的粒子的Energy-Momentum tensor. 我们可以推导出, 以spin 0的纯量场所描述的移动粒子, 其Energy-Momentum Tensor为:

 

也就是说, 如果一个粒子开始移动, 那麽他所受到的重力场强度会随着速度而变小. 这可能导致一些不自洽的结果.

 

Norbert Straumann提到一个忆想实验 , 来论证这个结果是错误的. 首先我们拿两个箱子, 里面各装 N个particle, 并且标上数字1和2. 然後用棒子将这两个箱子连起来., 这两个箱子会因为重力作用而互相吸引. 我们可以使这些力经过安排之後使得整个系统是静止的. 如果在2号箱子中有一个粒子的质量完全变为能量, 这时候虽然2号箱子的总质量应该不会改变, 不过由公式中我们会发现真正有作用的大小改变了. 由於纯量场的作用只跟Energy-Momentum Tensor的Trace有关系, 而这个变化可能会改变Energy-Momentum Tensor的 Trace大小, 而使得系统开始加速. 这个结果实在太方头了, 而且不合理.

 

二. spin 1/2 以及其他半整数spin的讨论:

 

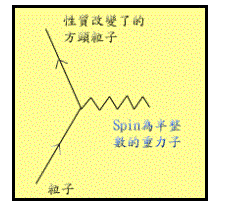文字方块: 如果一个粒子以1/2的粒子来做重力子, 这种重力子会是个费米子, 由於粒子在变动momentum的时候只能以1为单位, 如果这个粒子发出一个费米子, 那麽这个粒子就不能够只改变Lz, 而必须要改变本身的spin, 而使得内在性质改变, 这样是会造成大灾难的, 而且在实验中我们也没有看到一个家伙跟另一个家伙作用之後产生内在性质的改变.

 

　　如果我们坚持重力子必须是spin 1/2的粒子的话, 那麽一个粒子就必须要一次发出偶数个重力子才可以, 而在Feynman的讨论中, Feynman的结果是不管我们用多少的偶数重力子为单位, 我们都没有办法正确的描述广义相对论. 因此半整数spin就不再讨论了.

 

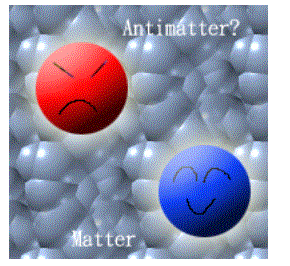文字方块: 叁. spin 1 以及spin为奇数的重力子的讨论:

 

        当我们考虑spin=1的粒子时, 我们直觉的想像这个量子场应该跟电磁场满像的, 因为光子也是spin 1的粒子. 而光子所代表的电磁作用具有相斥以及相吸两种作用. 因此我们可能要担心要如何去掉相斥的结果, 或者是要假设anti-matter的存在?

 

        依照Feynman Lecture on Gravitation前言的说法, 在spin 1, 3, 5等奇数倍spin的粒子来作为重力子, 都会获得糟糕的结果. 如果一个粒子与另一个相同的粒子, 带有相同的charge, 如果重力子带有的spin是奇数倍, 那麽我们就会得到相斥的结果. 然而如果我们是以spin为偶数的粒子来作为重力子, 那麽我们会得到一个有趣的结果 不管两个粒子所带的charge为相同或不同, 都会得到相吸的结果. 至於详细的推导, 已经超出我的能力 围.

 

四. Spin 2 重力子理论:

 

由前面的讨论发现, 我们能够做的选择只剩下spin 2的重力子了. Spin 2的重力理论是用 这样的对称二阶张量来描述, 因此我们有10个自由度. 根据Wigner的说法, 在无质量的情况下只有两个自由度, 因此我们要想办法让自由度减少到2个. Norbert Straumann在文章中做了讨论, 利用gauge invariant以及trace vanish的关系, 可以得到不错的结果.

 

而在文章中的讨论, 我们可以发现在Newtonian limit的状况下, Spin 2重立场能够描述得不错, 得到 与scalar field所得到的结果满相似的. Feynman利用与电磁场的相似性, 可以简单的导出与r平方成反比的energy, 给出正确的描述.

 

Norbert Straumann也在文章中提到spin 2的重力子能够与电磁场产生couple. 因此光子在重力场中不像是纯量场中所描述的不受影响, 而是会受到偏折. 产生重力透镜的效果.

 

        由於文章中所提到的概念已经超出我所能够理解的 围, 因此只能够这样做简单的描述.

 

Summary:

 

1.      重力子为什麽不能是spin 0 ? 因为spin 0所代表的场为纯量场, 不会跟光子产生interaction.

 

2.      重力子为什麽不能是spin1/2 或是其他半整数?: 因为spin 1/2以及半整数的重力子是费米子, 任何的粒子没有办法单独放出一个费米子, 如果argue可以放出两个或是其他偶数倍的费米子, Feynman的结果否决了这些猜测.

 

3.      重力子为什麽不能是 spin 1的或是其他奇数倍的呢?: 因为这种spin为奇数的家伙可能会造成相斥的力, 如光子就是spin 1, 会产生排斥力(电荷相同时). 而重力只有相吸而没有相斥.

 

4.      重力子为什麽可以是 spin 2 ? 因为重力子是spin 2可以成功的描述massless的粒子, 并且可以简单的推导出古典的r平方反比能量. 并且能够与电磁场couple, 产生interaction.

 

参考资料:

1.      Norbert Straumann, Reflection on Gravity

2.      黄伟彦, 粒子物理导论上课讲义.

3.      Feynman, Lecture on Gravitation

 

 


回物理领域介绍

回弦论首页