The Principle of Least Action

Jason Gross, December 7, 2010
Last Updated September 23, 2023

Introduction

Recall that we defined the Lagrangian to be the kinetic energy less potential energy, L=K-U, at a point.  The action is then defined to be the integral of the Lagrangian along the path,

It is (remarkably!) true that, in any physical system, the path an object actually takes minimizes the action.  It can be shown that the extrema of action occur at

This is called the Euler equation, or the Euler-Lagrange Equation.

Derivation

Courtesy of Scott Hughes’s Lecture notes for 8.033.  (Most of this is copied almost verbatim from that.)

Suppose we have a function of a variable x and its derivative .  We want to find an extremum of

Our goal is to compute x(t) such that J is at an extremum.  We consider the limits of integration to be fixed.  That is, will be the same for any x we care about, as will .

Imagine we have some x(t) for which J is at an extremum, and imagine that we have a function which parametrizes how far our current path is from our choice of x:

The function A is totally arbitrary, except that we require it to vanish at the endpoints: .  The parameter α allows us to control how the variation A(t) enters into our path x(t;α).

The “correct” path x(t) is unknown; our goal is to figure out how to construct it, or to figure out how f behaves when we are on it.

Our basic idea is to ask how does the integral J behave when we are in the vicinity of the extremum.  We know that ordinary functions are flat --- have zero first derivative --- when we are at an extremum.  So let us put

We know that α=0 corresponds to the extremum by definition of α.  However, this doesn’t teach us anything useful, sine we don’t know the path x(t) that corresponds to the extremum.

But we also know We know that since it’s an extremum.  Using this fact,

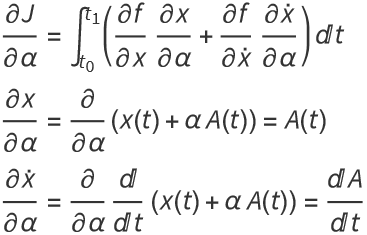
So

Integration by parts on the section term gives

Since , the first term dies, and we get

This must be zero.  Since A(t) is arbitrary except at the endpoints, we must have that the integrand is zero at all points:

This is what was to be derived.

Least action: F=m a

Suppose we have the Newtonian kinetic energy, , and a potential that depends only on position, .  Then the Euler-Lagrange equations tell us the following:

Rearrangement gives

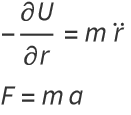
Least action with no potential

Suppose we have no potential, U=0.  Then L=K, so the Euler-Lagrange equations become

For Newtonian kinetic energy, , this is just

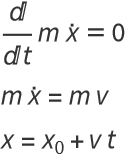
This is a straight line, as expected.

Least action with gravitational potential

Suppose we have gravitational potential close to the surface of the earth, U=m g y, and Newtonian kinetic energy, .  Then the Euler-Lagrange equations become

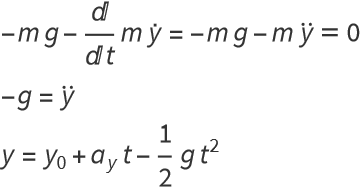
This is a parabola, as expected.

Constants of motion: Momenta

We may rearrange the Euler-Lagrange equations to obtain

If it happens that , then is also zero.  This means that is a constant (with respect to time).  We call a (conserved) momentum of the system.

Linear Momentum

By noting that Newtonian kinetic energy, , is independent of the time derivatives of position, if potential energy depends only on position, we can infer that (and, similarly, and ) are constant.  Then .  This is just standard linear momentum, m v.

Angular Momentum

Let us change to polar coordinates.

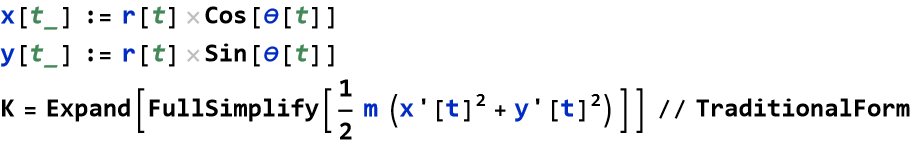
Using dot notation, this is

Note that θ does not appear in this expression.  If potential energy is not a function of θ (is only a function of r), then is constant.  This is standard angular momentum, .

Classic Problem: Brachistochrone (“shortest time”)

Problem

A bead starts at x=0, y=0, and slides down a wire without friction, reaching a lower point .  What shape should the wire be in order to have the bead reach in as little time as possible.

Solution

Idea

Use the Euler equation to minimize the time it takes to get from to .

Implementation

Letting ds be the infinitesimal distance element and v be the travel speed,

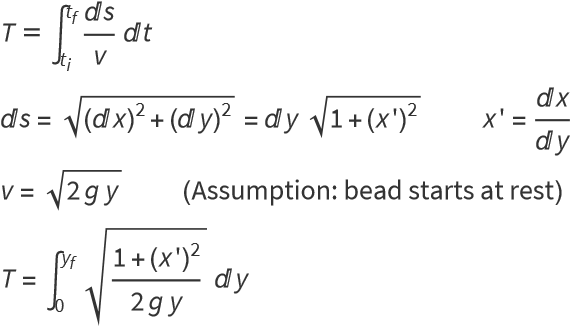
Now we apply the Euler equation to 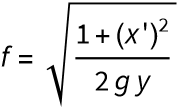and change t→y, .

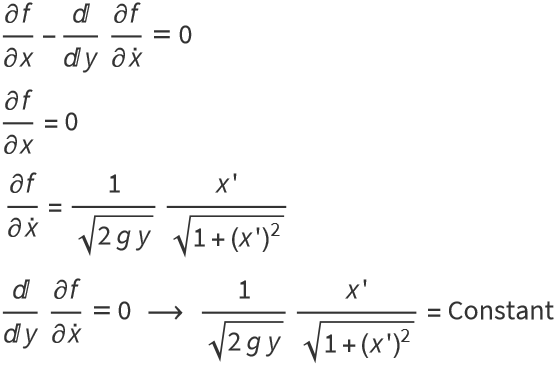
Squaring both sides and making a special choice for the constant gives

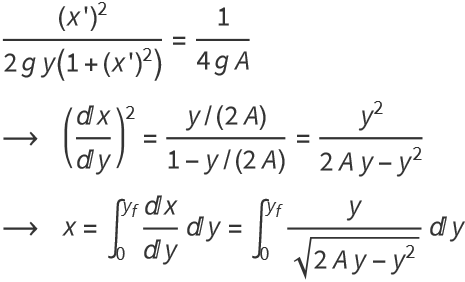
To solve this, change variables:

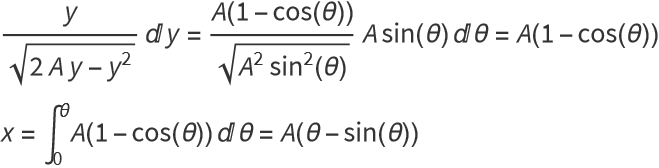
Full solution: The brachistochrone is described by

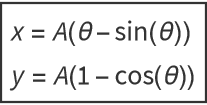
There’s no analytic solution, but we can compute them.

Classic Problem: Catenary

Problem

Suppose we have a rope of length l and linear mass density λ.  Suppose we fix its ends at points and .  What shape does the rope make, hanging under the influence of gravity?

Solution

Idea

Calculate the potential energy of the rope as a function of the curve, y(x), and minimize this quantity using the Euler-Lagrange equations.

Implementation

Suppose we have curve parameterized by t, (x(t), y(t)).  The potential energy associated with this curve is

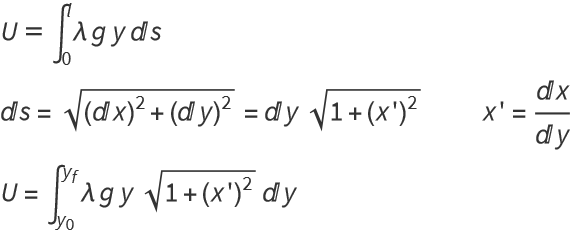
Note that if we choose to factor ds the other way (for y'), we get a mess.

Now we apply the Euler-Lagrange equation to and change t→y, .

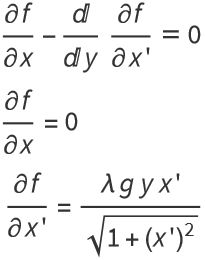
Since , is constant, say .  Then

Using the fact that

integration of x' gives

where b is a constant of integration.

Plotting this for a=1, b=0 gives:

Problem: Bead on a Ring

From 8.033 Quiz #2

Problem

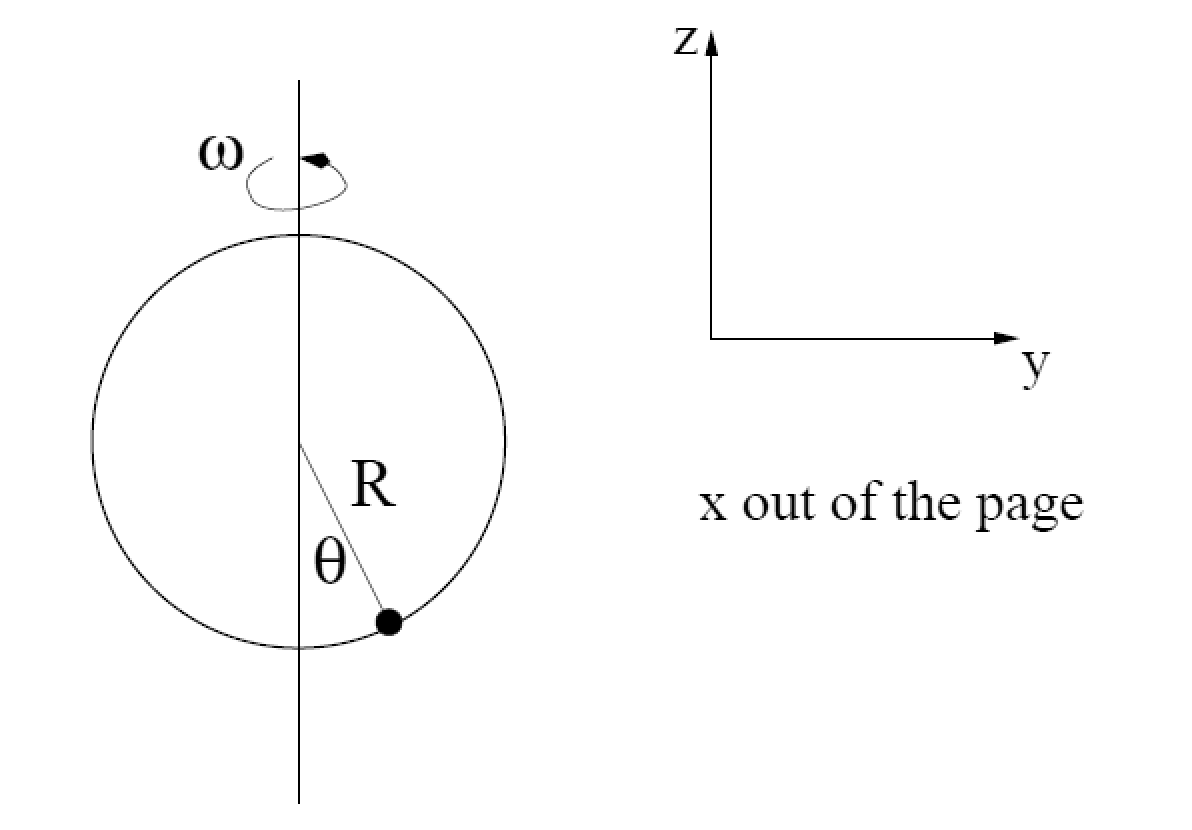
A bead of mass m slides without friction on a circular hoop of radius R. The angle θ is defined so that when the bead is at the bottom of the hoop, θ=0. The hoop is spun about its vertical axis with angular velocity ω. Gravity acts downward with acceleration g.
Find an equation describing how θ evolves with time.
Find the minimum value of ω for the bead to be in equilibrium at some value of θ other than zero.
(“equilibrium” means that and are both zero.) How large must ω be in order to make θ=π/2?

Solution

The general Lagrangian for the object in Cartesian coordinates is

Converting to polar coordinates, and using the constraints that φ=ω t and r=R, using the conversion

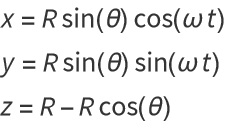
gives

Finding the minimum value of ω for the bead to be in equilibrium gives

In order for this to have a solution, we must have

If θ=π/2, then cos(θ)=0, so ω=∞.

Problem 11.8: K & K 8.12

Problem

A pendulum is rigidly fixed to an axle held by two supports so that it can only swing in a plane perpendicular to the axle. The pendulum consists of a mass m attached to a massless rod of length l. The supports are mounted on a platform which rotates with constant angular velocity Ω. Find the pendulum’s frequency assuming the amplitude is small.

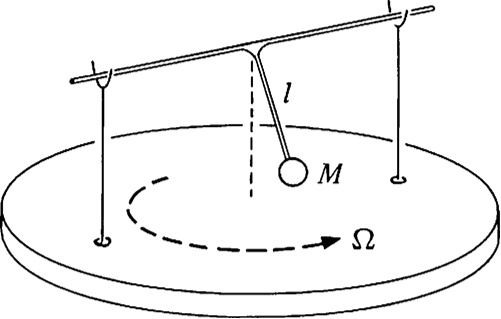
Solution by torque

(From the problem set solutions)

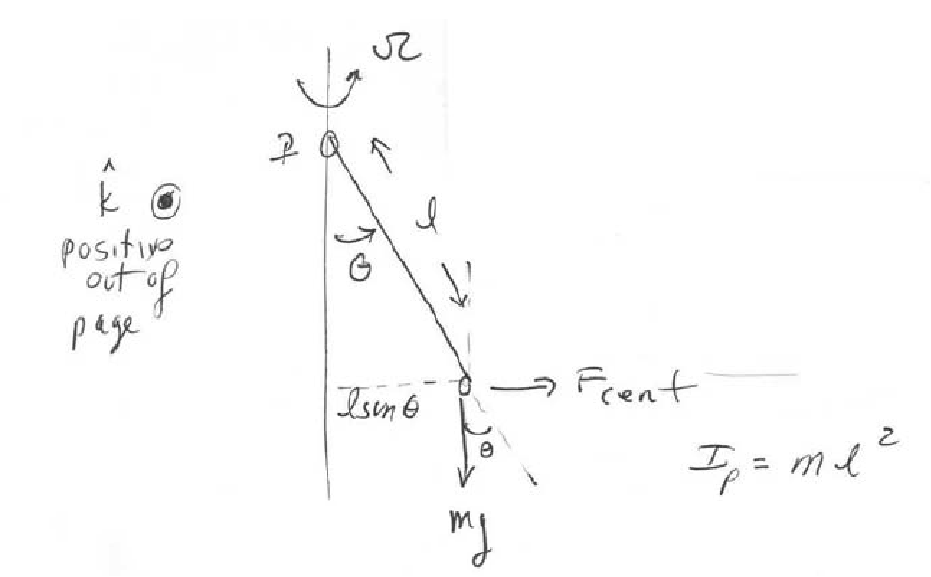
The torque about the pivot point is

The centrifugal effective force is

For small angles, sin(θ)=θ, cos(θ)=1.  Then equation (1) becomes

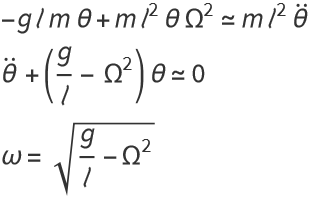
If , the motion is no longer harmonic.

Solution by least action

The general Lagrangian for the object in Cartesian coordinates is

Converting to polar coordinates, and using the constraints that φ=Ω t and r=ℓ, using the conversion

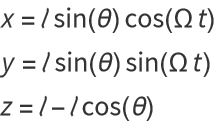
gives

Note that this is, after minor changes of variable, the exact same equation that we found in the previous problem.  We should(’ve) expect(ed) this.
Making the first order approximation that θ≈0 (Taylor expanding around θ=0 to the first order), we get

This is the differential equation for a harmonic oscillator, with

If , the motion is no longer harmonic.