Preliminary Concepts

An ordinary differential equation or ODE for short, may be thought of as a differential equality specifying the relationship between a dependent variable, say y, and an independent variable, say x. The order of the ODE is the order of the highest derivative of y with respect to x appearing in it. Hence, dy/dx + x² y =0 is a first order ODE whereas d² y/dx² + ky =0 is a second order ODE.

An ODE is linear if all the powers of y and its derivatives appearing in the ODE are non-negative integers not exceeding unity. The general equation for an nth order linear ODE is

$$a_n (x) \frac{d^ny}{dx^n} + a_{n-1}(x) \frac{d^{n-1}y}{dx^{n-1}} + ... + a_1(x)\frac{dy}{dx} + a_0(x) y = f(x).$$ (1)

The linear ODE of Eq. 1 is said to be homogeneous if $f(x)\equiv 0$.

We now make the distinction between the initial value problem (IVP) and the boundary value problem (BVP). This classification is based on the specification of supplementary data which enable us to arrive at a unique solution of the ODE. For the initial value problem, all the data (initial conditions) are specified at one point whereas for the boundary value problem the data are given as conditions on the boundary, i.e., as boundary conditions. Let's try to understand this through examples. For instance, consider the first order ODE dy/dx = y. The solution to this is a family of curves given by $y=A \exp(x)$. In order to uniquely determine the solution, we need to be given the value of y for some value of x. Suppose this was given by the condition y(0)=1. This determines A=1, hence the solution to the IVP

$$\frac{dy}{dx} = y, \:\:\: y(0) = 1$$ (2)

is given uniquely by $y = \exp (x)$. In the statement of the IVP above, we call the condition y(0) = 1 the initial condition. The origin of this terminology is from the correspondence of the independent variable x with time in many physical problems. For instance, according to classical mechanics, the motion of objects is governed by the second order IVP arising from Newton's second law

$$m\frac{d^2 x}{dt^2} = \sum_i F_i$$

$$\frac{dx}{dt} (t=0) = v_0$$

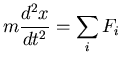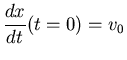x (t=0) = x₀, (3)

where x is the position of the object and t the time. Note that the IVP above has 2 initial conditions. In general, you need as many initial conditions as the order of the IVP to obtain a unique solution.

Note that we can write the second order IVP above (Eq. 3) as two first order ODEs plus one initial condition for each ODE. In order to achieve this, we define $v\equiv dx/dt$. Then the system of ODEs which represent the same IVP is

$$\frac{dv}{dt} = \sum_i F_i$$

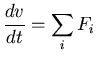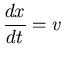$$\frac{dx}{dt} = v$$ v(t=0) = v₀ x(t=0) = x₀.

As an example of a boundary value problem (BVP), consider the following equation for the steady state temperature profile in a one-dimensional rod of length L, kept at a constant temperature at one end and insulated at the other, with a heat source/sink present within the rod.

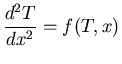$$\frac{d^2T}{dx^2} = f(T,x)$$ T(x=0) = T₁

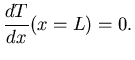$$\frac {dT}{dx} (x=L) = 0.$$ (4)

Note that the data are given at the two end points of the rod. These type of conditions are called boundary conditions and the BVP here describes the temperature profile within the rod subject to the boundary conditions specified above.

The ODE appearing in the BVP above (Eq. 5) looks very similar to the second order ODE appearing in the IVP in Eq. 3. However, from a mathematical perspective, these problems are very different, the difference arising primarily from the specification of the initial/boundary conditions. Hence, the algorithms for the numerical solution of IVPs and BVPs are significantly different as well.