


Next: Forward and Backward Euler
Up: 10.001: Numerical Solution of
Previous: Preliminary Concepts
Some of the key concepts associated with the numerical solution of IVPs are the
Local Truncation Error, the Order and the Stability of
the Numerical Method. We should also be able to distinguish explicit techniques
from implicit ones. In the following, these concepts will be introduced through
simple examples.
We are interested in the numerical solution of the IVP
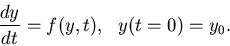 |
(5) |
In particular, if
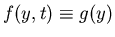 ,
the IVP above is called autonomous and if
g(y) = ky where k is a constant, the IVP is linear.
We assume that a unique solution exists and denote that solution by ye (t). So, for from
now on, y(t) refers to the numerically computed solution, which at the best is only an
approximation to ye(t).
,
the IVP above is called autonomous and if
g(y) = ky where k is a constant, the IVP is linear.
We assume that a unique solution exists and denote that solution by ye (t). So, for from
now on, y(t) refers to the numerically computed solution, which at the best is only an
approximation to ye(t).
Michael Zeltkevic
1998-04-15