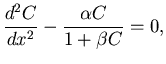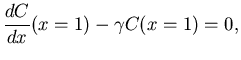Next: About this document ...
Up: Boundary Value Problems: The
Previous: Boundary Value Problems: The
Consider the following non-linear BVP in the x domain [0,1] given by
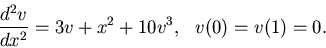 |
(37) |
Once again, let's divide the domain into n equal intervals of length h.
Using the finite difference approximation given in Eq. 32, we get
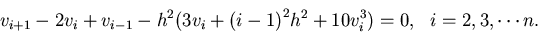 |
(38) |
The boundary conditions give the remaining two equations, i.e., v1 = 0 and
vn+1 = 0.
The FD equations for the non-linear problem above differ from those obtained for the linear BVP
(compare Eqs. 36 with 39). The FD approximation of the linear BVP results in a
system of linear equations whereas that of the non-linear BVP results
in a system of non-linear equations. In Eq. 39, the non-linearity arises
from the cubic term in v present in the BVP. The the solution of the n+1 non-linear
equations can be obtained using Newton's method where the unknowns are
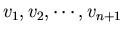 .
Recall that Newton's method is iterative, and it
requires the solution of a system of linear equations at every iteration step.
Once again we see that the solution of a system of linear equations is indeed a
central problem of scientific computing.
.
Recall that Newton's method is iterative, and it
requires the solution of a system of linear equations at every iteration step.
Once again we see that the solution of a system of linear equations is indeed a
central problem of scientific computing.
Exercise Problems
1a. Show that the FD equations (Eq. 39) can be rewritten as n-1 equations in n-1 unknowns
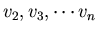 using the fact that the boundary conditions imply
v1 = vn+1 = 0.
Name the n-1 unknowns as
using the fact that the boundary conditions imply
v1 = vn+1 = 0.
Name the n-1 unknowns as
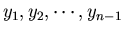 where y1 = v2,
where y1 = v2,
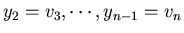 .
.
1b. Express the equations using the vector notation in the form
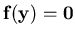 ,
where
,
where
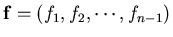 and
and
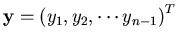 .
For instance, the
the first equation (f1 = 0) should read
y2 - 2y1 - h2(3y1 + h2 + 10y13) = 0.
.
For instance, the
the first equation (f1 = 0) should read
y2 - 2y1 - h2(3y1 + h2 + 10y13) = 0.
1c. Derive the Jacobian matrix
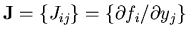 for the
above system of equations (refer to the notes on Newton's method).
for the
above system of equations (refer to the notes on Newton's method).
2. The non-linear BVP given below represents a reaction-diffusion process with non-linear
chemical reaction kinetics.
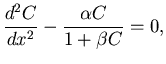 |
|
|
|
| C(x=0) = 1, |
|
|
|
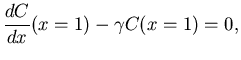 |
|
|
(39) |
where 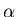 ,
,
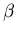 and
and 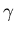 are positive constants and
are positive constants and
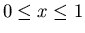 .
Develop the FD equations (based on Eqs. 32 and 33) for the above BVP.
How can we solve the system of equations?
.
Develop the FD equations (based on Eqs. 32 and 33) for the above BVP.
How can we solve the system of equations?



Next: About this document ...
Up: Boundary Value Problems: The
Previous: Boundary Value Problems: The
Michael Zeltkevic
1998-04-15