Let's consider the linear BVP describing the steady state concentration profile C(x)
in the following reaction-diffusion problem in the domain
![]() .
The BVP can be stated as
.
The BVP can be stated as
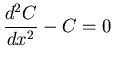 |
|||
| C(x=0) = 1 | |||
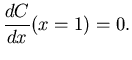 |
(30) |
We are interested in solving the above equation using the FD technique. The first step is
to partition the domain [0,1] into a number of sub-domains or intervals of length h. So, if
the number of intervals is equal to n, then nh = 1. We denote by xi the interval end points or
nodes, with
x1 =0 and
xn+1 = 1. In general, we have
xi = (i-1)h,
![]() .
Let us denote the concentration at the ith node by Ci.
The second step is to express the differential
operator d2C/dx2 in a discrete form. This can be accomplished using finite difference
approximations to the differential operators. In this problem, we will use the approximation
.
Let us denote the concentration at the ith node by Ci.
The second step is to express the differential
operator d2C/dx2 in a discrete form. This can be accomplished using finite difference
approximations to the differential operators. In this problem, we will use the approximation
| (31) |
| (32) |
Let's now derive the discretized equations. First of all,
we have two boundary conditions to be implemented. The boundary condition at
x=0 gives
| C1 = 1 | (33) |
| (34) |
So far, we have supplied 2 equations for the n+2 unknowns, the remaining n equations are obtained by
writing the discretized ODE for nodes
![]() .
Application of Eq. 32 and the use of the boundary conditions lead to the following
system of linear equations for Ci,
.
Application of Eq. 32 and the use of the boundary conditions lead to the following
system of linear equations for Ci,
![]() .
.
| C1 = 1 | |||
| C3 - (2+h2) C2 + C1 = 0 | |||
| C4 - (2+h2)C3 + C2 = 0 | |||
| .................... | |||
| Cn+2 - (2+h2)Cn+1 + Cn = 0 | |||
| Cn+2 - Cn = 0. | (35) |
We can express this
system compactly using matrices.
The
![]() coefficient matrix, say
coefficient matrix, say ![]() ,
corresponding to the system of equations
given above is
,
corresponding to the system of equations
given above is
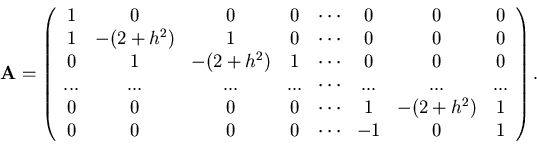 |
(36) |
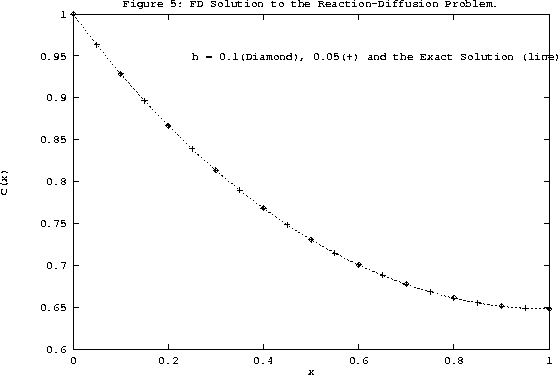
In Figure 5, the FD solution with h=0.1 and h=0.05 are presented along with the exact
solution to the BVP of Eq. 31. A very good agreement between the exact and the computed
solutions can be seen from there.
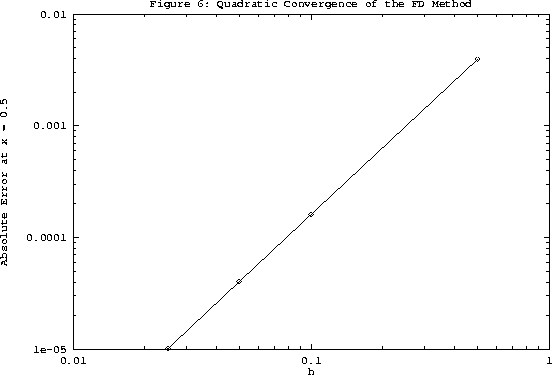
How does the FD scheme above converge to the exact solution as h is decreased? The absolute
error at the center of the domain (x=0.5) for three different values of h are plotted vs. h
in Figure 6 on a log-log plot. It can be seen from there that the error decreases as
O(h2). Hence, the FD approximation used here has quadratic convergence. This is
because the discretization errors in the approximation of the first and second derivative operators
(see Eqs. 32 and 33) are O(h2). Indeed, the convergence characteristics can be improved
by using more accurate discretization of the differential operators.