


Next: Boundary Value Problems: The
Up: 10.001: Numerical Solution of
Previous: Predictor-Corrector Methods
It was mentioned in the introduction (see Eq. 4) that systems of first order ODEs can arise from
a single ODE of order larger than unity. Systems of ODEs also arises naturally from physical
modeling. For instance, the following IVP describes the concentrations yi,
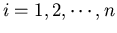 of
n chemicals in a reactor as a function of time.
of
n chemicals in a reactor as a function of time.
| |
|
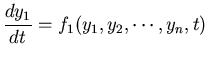 |
|
| |
|
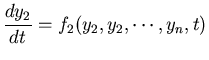 |
|
| |
|
.................................... |
|
| |
|
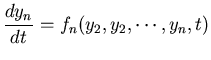 |
|
| |
|
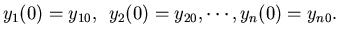 |
(26) |
The methods we discussed for the solution of a single first order ODE can be extended to the system of ODEs.
Let's define the n-dimensional vector of solutions
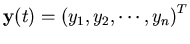 and the
n dimensional vector of the right hand side functions
and the
n dimensional vector of the right hand side functions
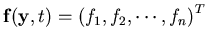 .
Similarly, the initial conditions can be arranged in a vector
.
Similarly, the initial conditions can be arranged in a vector
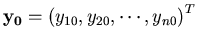 .
This allows us to write the IVP in the vector notation as
.
This allows us to write the IVP in the vector notation as
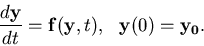 |
(27) |
Now, if we apply the forward Euler method for the solution of Eq. 28, with constant time step size h, we get
the following explicit equation for the solution at the (k+1)th step given the solution at the k the step:
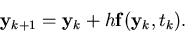 |
(28) |
However, the implicit backward Euler method gives
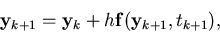 |
(29) |
which necessitates in general the solution of a system of non-linear algebraic equations at every time step.
We can employ Newton's method for a system of non-linear equations to achieve this.



Next: Boundary Value Problems: The
Up: 10.001: Numerical Solution of
Previous: Predictor-Corrector Methods
Michael Zeltkevic
1998-04-15
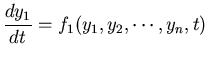
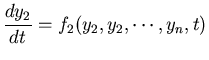
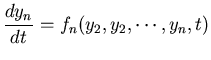
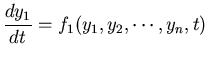
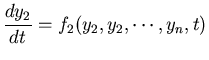
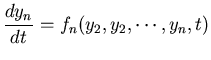
![]() and the
n dimensional vector of the right hand side functions
and the
n dimensional vector of the right hand side functions
![]() .
Similarly, the initial conditions can be arranged in a vector
.
Similarly, the initial conditions can be arranged in a vector
![]() .
This allows us to write the IVP in the vector notation as
.
This allows us to write the IVP in the vector notation as