Predictor-Corrector Methods

The idea behind the predictor-corrector methods is to use a suitable combination of an explicit and an implicit technique to obtain a method with better convergence characteristics. The combination of the FE and the AM2 methods is employed often. Here, we use the FE as a predictor equation to get y^p_n+1 and subsequently use the AM2 as a corrector equation to get the final computed solution y_n+1. The method, referred to as the Euler-Trapezoidal method is given below.

$$y^p_{n+1} = y_n + h f(y_n,t_n)\:\: {\mbox{Predictor}}$$

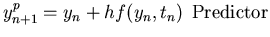$$y_{n+1} = y_n + \frac{h}{2}\left[ f(y^p_{n+1},t_{n+1})+f(y_n,t_n)\right]\:\:{\mbox{Corrector}}.$$ (24)

Note that in the second (corrector) step, the implicit term for the AM2, f(y_n+1,t_n+1) is replaced with f(y^p_n+1,t_n+1), i.e., the value of f evaluated at the predicted y^p_n+1 is used. Hence, the predictor-corrector method described above is an explicit method.

Exercise Problem

Consider the IVP

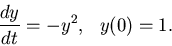$$\frac{dy}{dt} = -y^2, \:\:\: y(0) = 1.$$ (25)

Write C programs to compute y(t) in the interval [0,2] using (a). the forward Euler method (b) the AB2 method (c). the Euler-Trapezoidal (predictor-corrector) method and (d). the RK4 method. Plot your numerically computed solutions with h=0.1 along with the exact solution y=1/(1+t). Compare the convergence properties of each one of the above methods by plotting the absolute error for y(2) for h=0.001, 0.01 and 0.1. How do the stability characteristics of these methods compare with one another?