Adams Methods

From the IVP of Eq. 6, we can write

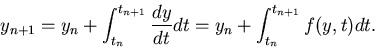$$y_{n+1} = y_n + \int_{t_n}^{t_{n+1}} \frac{dy}{dt} dt = y_n + \int_{t_n}^{t_{n+1}} f(y,t) dt.$$ (21)

Adams methods are based on the idea of approximating the integrand with a polynomial within the interval (t_n, t_n+1). Using a kth order polynomial results in a k+1th order method. There are two types of Adams methods, the explicit and the implicit types. The explicit type is called the Adams-Bashforth (AB) methods and the implicit type is called the Adams-Moulton (AM) methods.

The first order AB and AM methods are simply the forward and the backward Euler methods respectively. The second order versions (obtained by using a linear interpolant) of these methods are quite popular. The second order Adams-Bashforth (AB2) method is given by

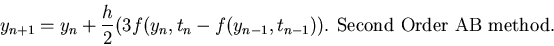$$y_{n+1} = y_n + \frac{h}{2}(3 f(y_n,t_n - f(y_{n-1}, t_{n-1})). \:\: {\mbox{Second Order AB method.}}$$ (22)

Note that the AB2 method is explicit and hence only conditionally stable. Moreover, the AB2 method requires the solution from the n-1th and the nth steps to find the solution at the n+1th step.

The second order Adams-Moulton (AM2) is an implicit technique, sometimes referred to as the trapezoidal rule. The time-stepping equation for AM2 is given by

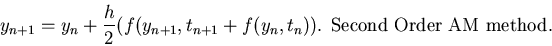$$y_{n+1} = y_n + \frac{h}{2}(f(y_{n+1}, t_{n+1}+f(y_n,t_n)). \:\: {\mbox{Second Order AM method.}}$$ (23)

The implicit nature of the method is evident from Eq. 24. For a non-linear IVP, we have to solve a non-linear algebraic equation at every time step. This is much more expensive as compared to the explicit AB2 method. However, being an implicit technique, AM2 does not suffer from the numerical instability of the AB2 for relatively large values of the time step. Once again, it is a trade-off between stability and computational cost, since both AM2 and AB2 are second order accurate.