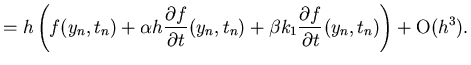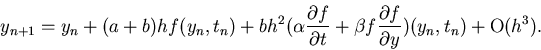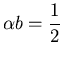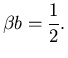Next: Adams Methods
Up: Higher Order Methods
Previous: Higher Order Methods
In the forward Euler method, we used the information on the slope or the derivative of y
at the given time step to extrapolate the solution to the next time-step. The LTE for the
method is O(h2), resulting in a first order numerical technique. Runge-Kutta methods
are a class of methods which judiciously uses the information on the 'slope' at more than one point
to extrapolate the solution to the future time step. Let's discuss first the derivation of
the second order RK method where the LTE is O(h3).
Given the IVP of Eq. 6, and a time step h, and the solution yn at the nth time step,
let's say that we wish to compute yn+1 in the following fashion:
| |
|
k1 = hf(yn,tn) |
|
| |
|
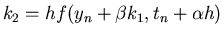 |
|
| |
|
yn+1 = yn + ak1 + bk2, |
(12) |
where the constants 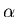 ,
,
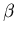 ,
a and b have to be evaluated so that the
resulting method has a LTE O(h3). Note that if k2=0 and a=1, then Eq. 13 reduces
to the forward Euler method.
,
a and b have to be evaluated so that the
resulting method has a LTE O(h3). Note that if k2=0 and a=1, then Eq. 13 reduces
to the forward Euler method.
Now, let's write down the Taylor series expansion of y in the neighborhood of tn correct to
the h2 term i.e.,
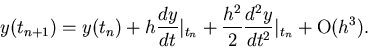 |
(13) |
However, we know from the IVP (Eq. 6) that
dy/dt = f(y,t) so that
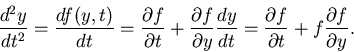 |
(14) |
So from the above analysis, i.e., Eqs. 14 and 15, we get

+ {\mbox{O}}(h^3).
\end{displaymath}](img38.gif) |
(15) |
However, the term k2 in the proposed RK method of Eq. 13 can be expanded correct to O(h3) as
| |
|
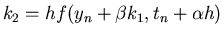 |
|
| |
|
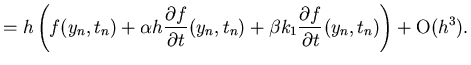 |
(16) |
Now, substituting for k2 from Eq. 17 in Eq. 13, we get
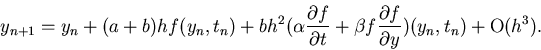 |
(17) |
Comparing the terms with identical coefficients in Eqs. 16 and 18 gives us the following system of equations to
determine the constants:
| |
|
a+b=1 |
|
| |
|
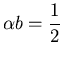 |
|
| |
|
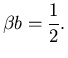 |
(18) |
There are infinitely many choices of a, b,  and
and  which satisfy Eq. 19, we can choose for instance
which satisfy Eq. 19, we can choose for instance
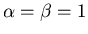 and a=b=1/2. With this choice, we have the classical second order accurate Runge-Kutta
method (RK2) which is summarized as follows.
and a=b=1/2. With this choice, we have the classical second order accurate Runge-Kutta
method (RK2) which is summarized as follows.
| |
|
k1 = hf(yn,tn) |
|
| |
|
k2 = hf(yn+k1, tn + h) |
|
| |
|
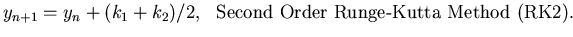 |
(19) |
In a similar fashion Runge-Kutta methods of higher order can be developed. One of the most widely used methods for the
solution of IVPs is the fourth order Runge-Kutta (RK4) technique. The LTE of this method is order h5.
The method is given below.
| |
|
k1 = hf(yn,tn) |
|
| |
|
k2 = hf(yn+k1/2, tn + h/2) |
|
| |
|
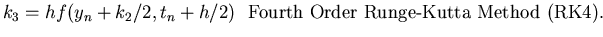 |
|
| |
|
k4 = h(yn+k3, tn + h) |
|
| |
|
yn+1 = yn + (k1 + 2k2 + 2k3 + k4)/6. |
(20) |
Note that the RK methods are explicit techniques, hence they are only conditionally stable.



Next: Adams Methods
Up: Higher Order Methods
Previous: Higher Order Methods
Michael Zeltkevic
1998-04-15
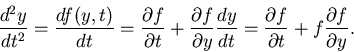

+ {\mbox{O}}(h^3).
\end{displaymath}](img38.gif)