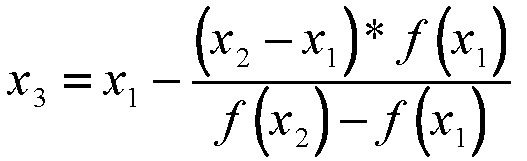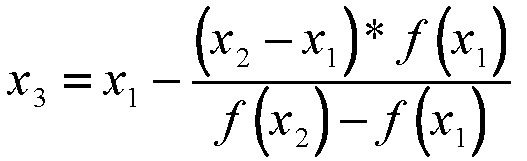

Next: Newton-Raphson
Technique Up: 10.001:
Solution of Non-Linear Previous: Convergence
The Method of False Position
The poor convergence of the bisection method as well as its poor adaptability
to higher dimensions (i.e., systems of two or more non-linear equations)
motivate the use of better techniques. One such method is the Method
of False Position. Here, we start with an initial interval [x1,x2],
and we assume that the function changes sign only once in this interval.
Now we find an x3 in this interval, which is given by
the intersection of the x axis and the straight line passing through (x1,f(x1))
and (x2,f(x2)).
It is easy to verify that x3 is given by
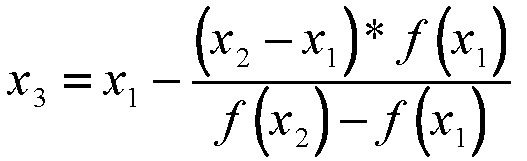 |
(4) |
Now, we choose the new interval from the two choices [x1,x3]
or [x3,x2] depending on in which interval
the function changes sign.
The false position method differs from the bisection method only in
the choice it makes for subdividing the interval at each iteration. It
converges faster to the root because it is an algorithm which uses appropriate
weighting of the intial end points x1 and x2
using the information about the function, or the data of the problem. In
other words, finding x3 is a static procedure
in the case of the bisection method since for a given x1
and x2, it gives identical x3,
no matter what the function we wish to solve. On the other hand, the false
position method uses the information about the function to arrive at x3.


Next: Newton-Raphson
Technique Up: 10.001:
Solution of Non-Linear Previous: Convergence
Mark D Smith
1998-10-01