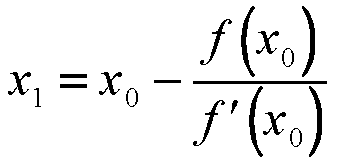 |
(6) |
Unlike the bisection and false position methods, the Newton-Raphson (N-R) technique requires only one inital value x0, which we will refer to as the initial guess for the root. To see how the N-R method works, we can rewrite the function f(x) using a Taylor series expansion in (x-x0):
| f(x) = f(x0) + f'(x0)(x-x0) + 1/2 f''(x0)(x-x0)2 + ... = 0 | (5) |
where f'(x) denotes the first derivative of f(x) with respect to x, f''(x) is the second derivative, and so forth. Now, suppose the initial guess is pretty close to the real root. Then (x-x0) is small, and only the first few terms in the series are important to get an accurate estimate of the true root, given x0. By truncating the series at the second term (linear in x), we obtain the N-R iteration formula for getting a better estimate of the true root:
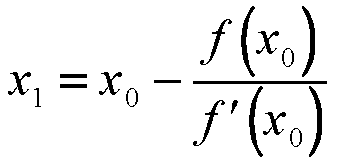 |
(6) |
Thus the N-R method finds the tangent to the function f(x) at x=x0 and extrapolates it to intersect the x axis to get x1. This point of intersection is taken as the new approximation to the root and the procedure is repeated until convergence is obtained whenever possible. Mathematically, given the value of x = xi at the end of the ith iteration, we obtain xi+1 as
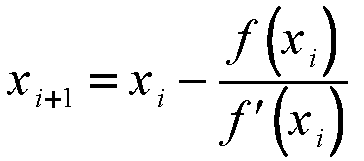 |
(7) |
We assume that the derivative does not vanish for any of the xk,
k=0,1,..., i+1. The result obtained from this method with x0
= 0.1 for the equation of Example 1, 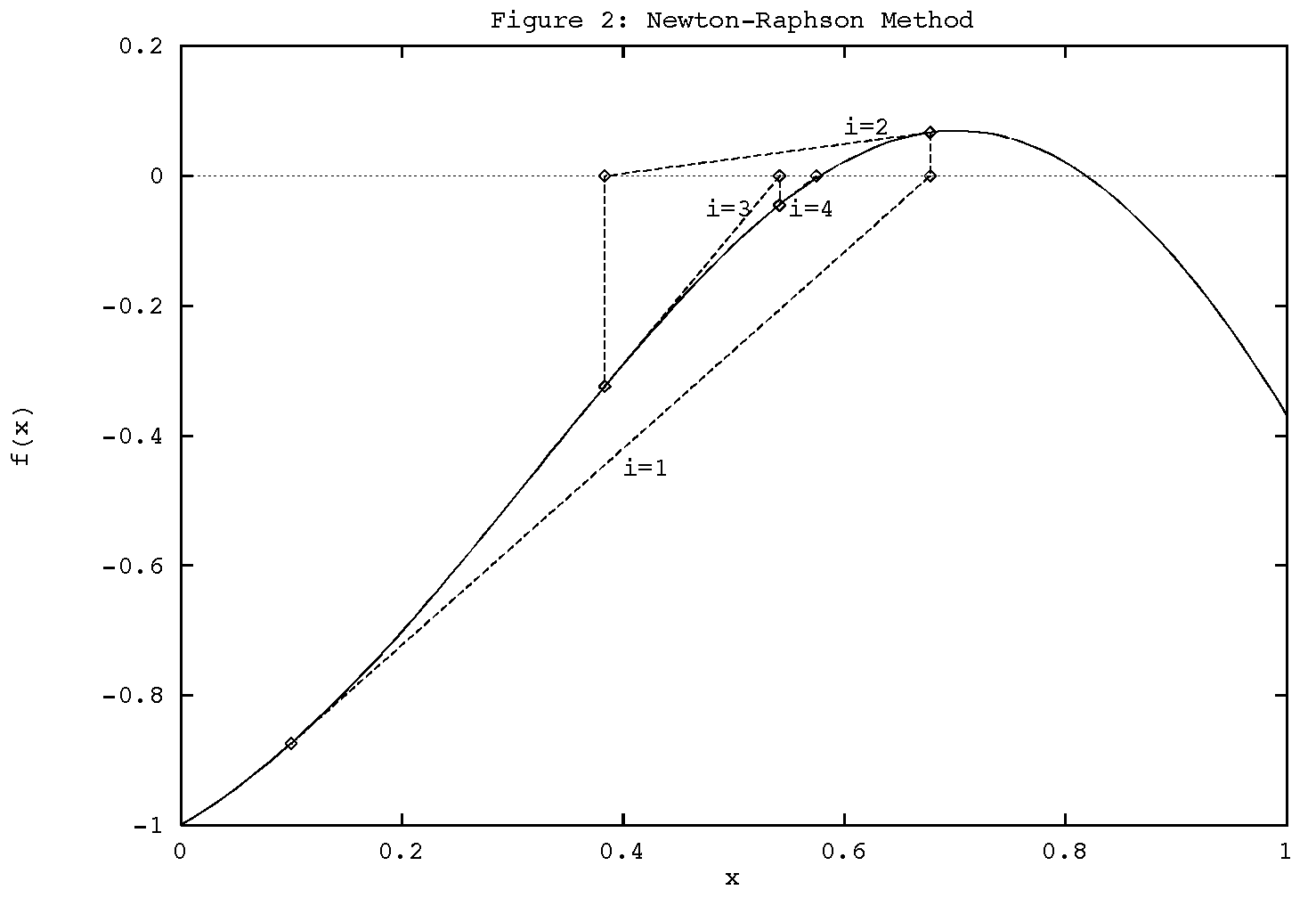
Here also, when multiple roots are present, the root evenutally identified
by the algorithm depends on the starting conditions supplied by the user.
For example, if we had started with x0 = 0.0, the N-R
method will converge to the larger root, as shown in Figure 3.
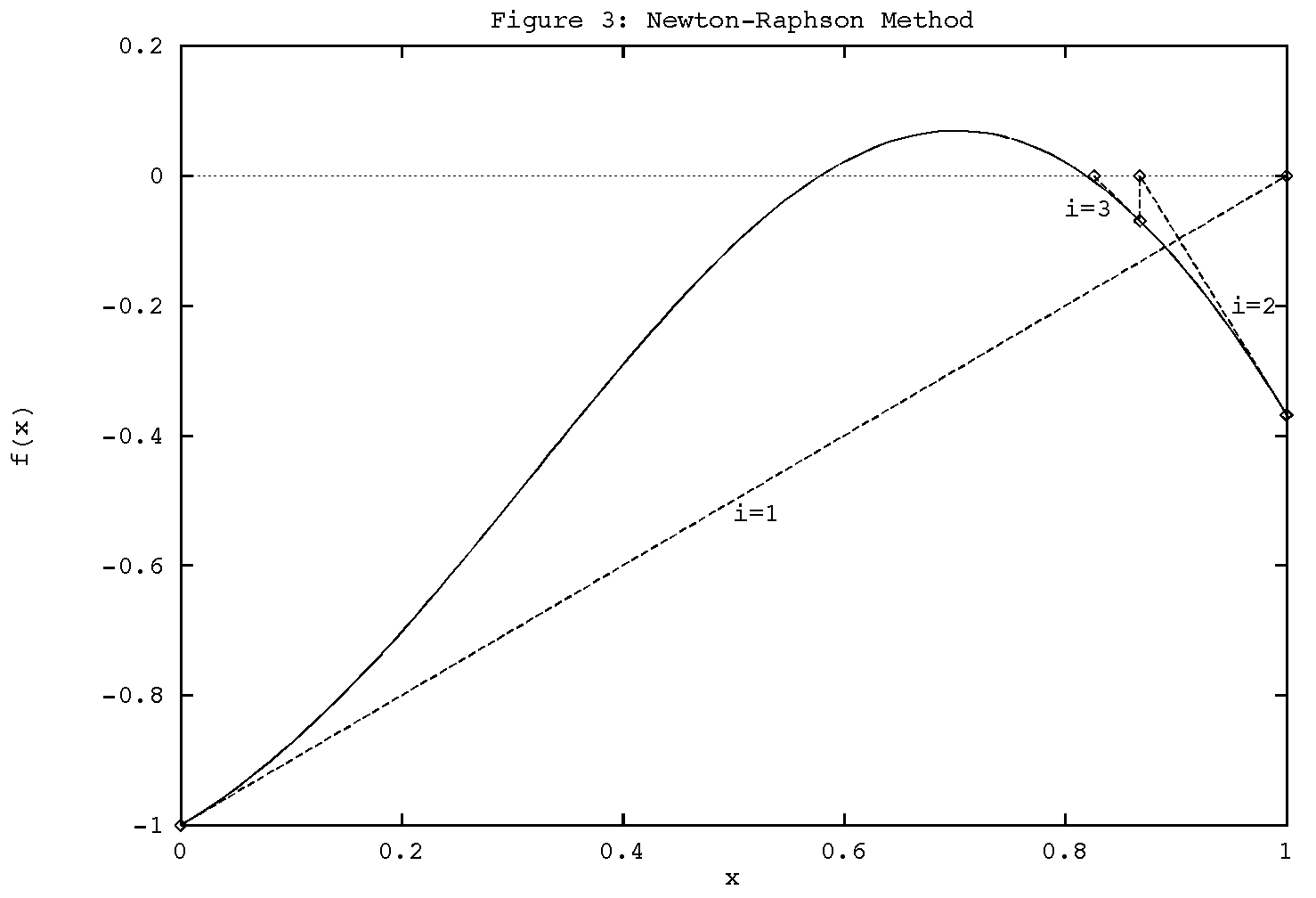
So, before using any of the methods, we should try to get as good a
feel as we can afford to get for the function. An approximate idea of the
roots can be developed from the physics the equation represents, preliminary
mathematical analysis and using plotting routines.