... example.¹

See /mit/10.001/Examples/MapleTutorial/figures.ms for figures which are referred to in this document. Note that figures.ms is a maple file. Copy this into your working directory, load it into a maple session and print it.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... as²

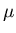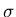Note that the sample variance is defined with n - 1 in the denominator, if we use n instead of n - 1 in Eq. 2, the quantity computed is referred to as the population variance. For large values of n, the sample variance is practically equal to the population variance. Here, the same symbols, $\mu$ and $\sigma$, are used to denote the mean and standard deviation respectively of the sample and the population. This is not to imply that they are the same, the sample mean and variance provide at the best an estimate of the population mean and variance. We will make the distinction between the sample and the population statistics from the context.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.