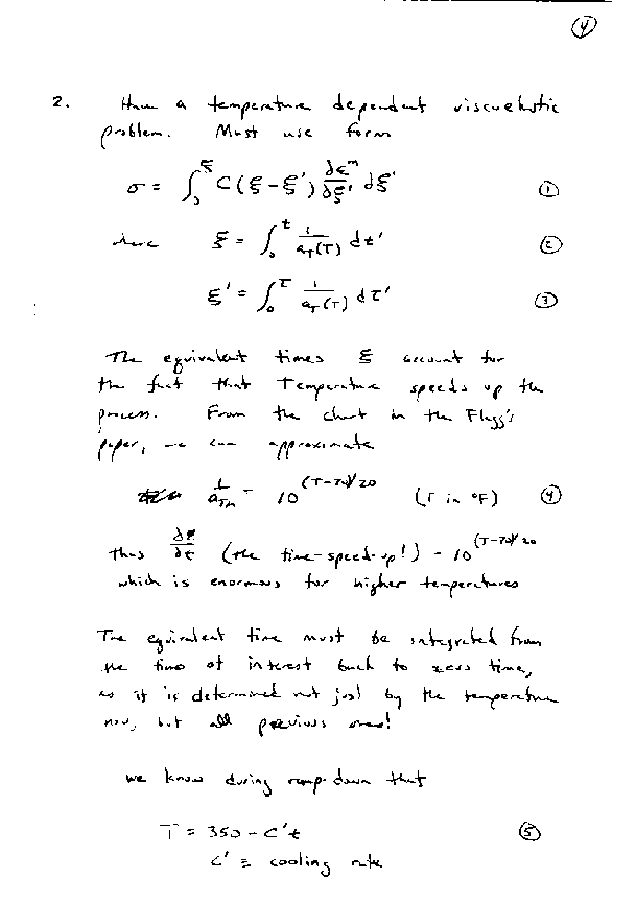
| Return to PS list |
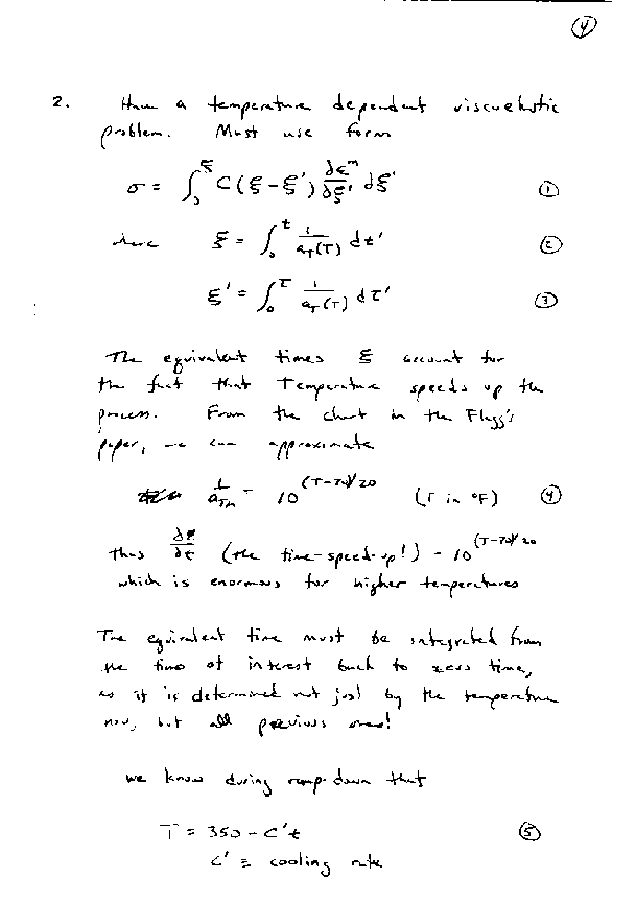


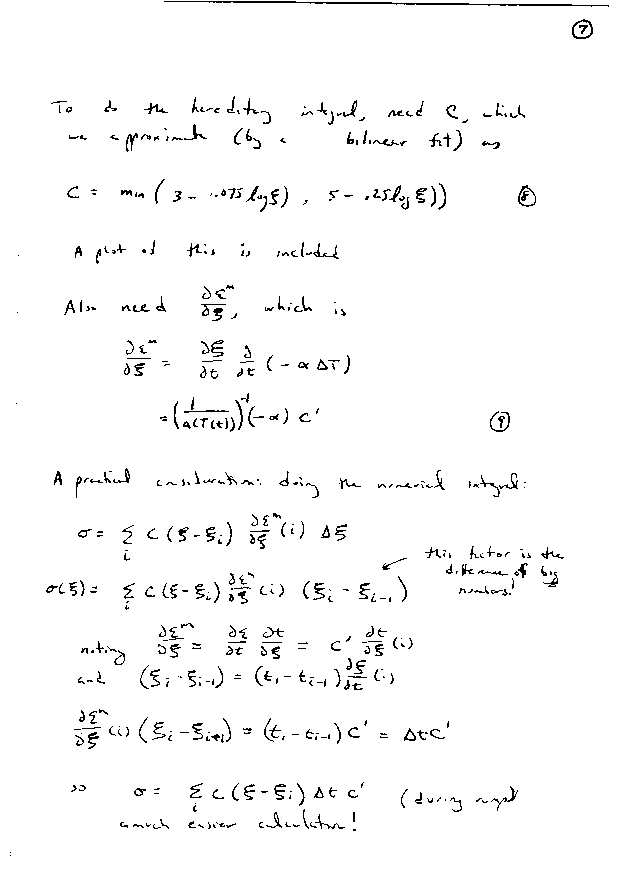
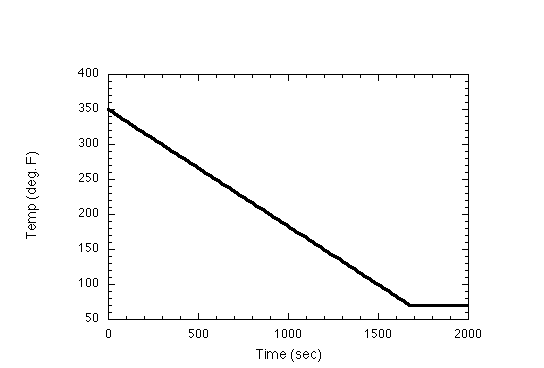
The following are example plots of the temperature as a function of time (at 10 deg.F/min), the factor aTM as a function of temperature (a linear fit to the plot in the paper), the relaxation modulus as a function of equivalent time elapsed (a bi-linear fit to the plot in the paper), and the equivalent time as a function of time (again, for a 10 deg F/min cooldown)
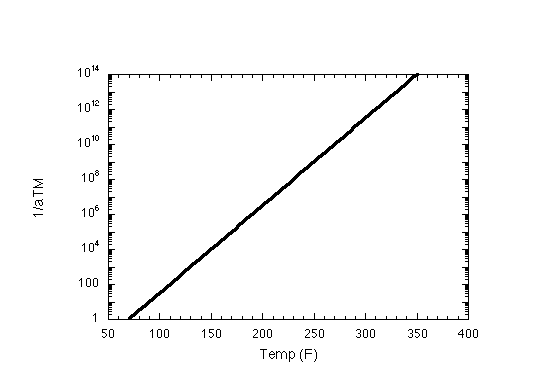
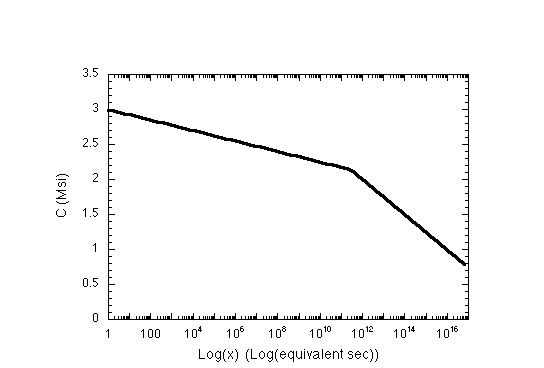
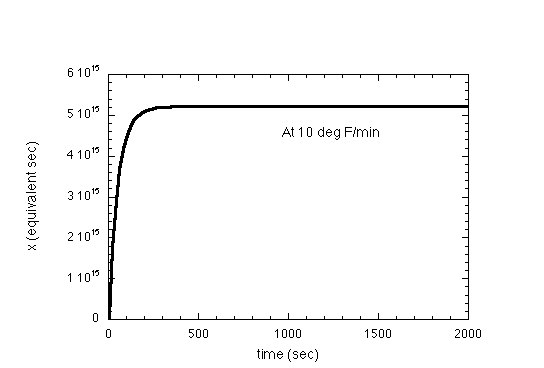
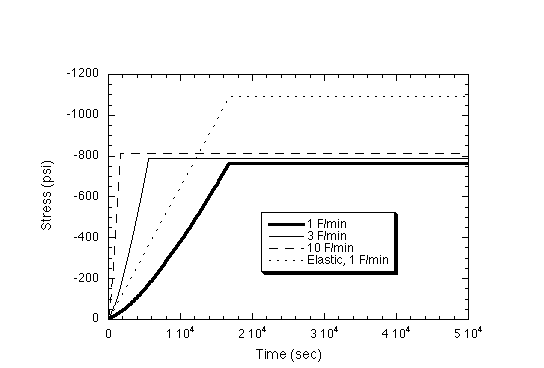
At last, results. Also included elastic responce at 1 F/min for comparison. See that viscoelastic effects are significant, but not very sensative to the ramp rate.
Finally, code.
character*1 tab
double precision time(1000), Temp(1000), x(1000), xx(1000),
+oneoverat(1000), dedx(1000), C(1000), stress(1000)
c set cprime (in F/sec), other fixed stuff
tab = char(09)
cprime = 10./60.
alpha = 1.3
dt = 280/cprime/800
deps = - dt * cprime*alpha
c set times to check. Lots of steps on the ramp
c plus a bunch after its over.
c Also, do T and x (squiggle), from the curve fits
c and integral calcs in the written solution,
c and compute time-speed-up and strain increments
time(1) = 0.
temp(1) = 350
x(1) = 0
C(1) = 3.
oneoverat(1) = 10.**14
dedx(1) = -cprime*alpha/oneoverat(1)
c during ramp (800 steps!) F_DoBackground call just makes this act
c like a proper Mac application
do 1 i = 1, 800
write (6,801) i
CALL F_DoBackground
time(i+1) = dt * i
Temp(i+1) = 350-cprime*time(i+1)
x(i+1) = 1.e+14/(log(10.)*cprime/20)*(1-10**(-cprime*time(i+1)/20.))
oneoverat(i+1) = 10**((Temp(i-1)-70)/20)
1 dedx(i) = -cprime*alpha/oneoverat(i+1)
c after ramp (200 steps, one/day)
do 2 i = 802,1000
write (6,801) i
CALL F_DoBackground
time(i) = time(801) + (i-801) * 3600*24
Temp(i) = 70
x(i) = x(801) + time(i) - time(801)
oneoverat(i) = 1
2 dedx(1) = 0
c now compute a table of C vs x values. This is just for plotting.
xx(1) = 0
C(1) = 3
do 3 i = 2, 1000
xx(i) = 10**((i-1)/1000.*17.)
3 C(i) = GETC(xx(i))
c do hereditary integral
stress(1) = 0
c calculate stress at each time i
do 200 i = 2,1000
write (6,802) i
CALL F_DoBackground
stress(i) = 0
c do so by summing over all the strain increments at times
c j that go from zero to now (time i); each multipled by
c the C value for the time from the strain (j) to now (i)
c also note here an avoid to numerical problems- the factor
c x(j+1)-x(j) is the difference between two huge numbers, and will
c go incorrectly to -> 0 for large times. We note for constant
c time steps that the the strain step is also constant, and just
c use it (see notes). After ramp (j>800) no deps, so no additional
c stess, but note that we still do these calcs even for i>800
c because the x(i)-x(j) terms continue to change
c the 'old' way is commented out below-
do 100 j = 1, min((i-1),800)
stress(i) = stress(i) + deps * GETC(x(i)-x(j))
100 continue
c do 100 j = 1, i-1
c 100 stress(i) = stress(i) + (x(j+1)-x(j)) * dedx(j) * GETC(x(i)-x(j))
200 continue
c big dump of everything in a tab-separated set of columns
c only do one out of every 10!
do 300 i = 1, 1000, 10
300 write (6,800) time(i), tab, x(i), tab, Temp(i), tab, oneoverat(i),
+ tab, dedx(i), tab, stress(i), tab, xx(i), tab, C(i)
800 format(1x, 1pd11.3, 7(a1, 1pd11.3))
801 format ('+ set up ',i3)
802 format ('+ stress calcs ',i3)
c that's all folks!
stop
end
C
DOUBLE PRECISION FUNCTION GETC(X)
DOUBLE PRECISION X
C
getc = min((3.-.075*log10(x)),(5.-.25*log10(x)))
RETURN
END
C