Thermodynamics and Propulsion

18.4 Some Considerations in Modeling Complex Physical Processes

In Sections 18.2 and 18.3, a number of assumptions were made about the processes that we were attempting to describe. These are all part of the general approach to modeling of physical systems. The main idea is that for engineering systems, one almost always cannot compute the process exactly, especially for fluid flow problems. At some level of detail, one generally needs to model, i.e. to define some plausible behavior for attributes of the system that will not be computed.

Modeling can span an enormous range from the level of our assumption of uniform temperature within the solid object to a complex model for the small scale turbulent eddies in the flow past a compressor blade. In carrying out such modeling, it is critical to have a clear idea of just what the assumptions really mean, as well as the fidelity that we ascribe to the descriptions of actual physical phenomena, and we thus look at the statements we have made in this context.

One assertion made was that because $hL/k \ll 1$ and on the basis of a heat balance,

$$\frac{k}{L}(T_c -T_w) \approx h(T_w-T_\infty),$$

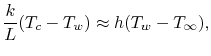
we could assume

$$\frac{(T_\textrm{body interior} - T_w)}{(T_w-T_\infty)} \ll 1.$$

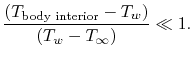
Based on this, we said that $T_\textrm{body}$ is approximately uniform and $T_w \approx T_\textrm{body interior}$ . Another aspect is that setting $hA/Pk \ll 1$ erases any geometrical detail of the fin cross section. The only place where $P$ and $A$ enter the problem is in a non-dimensional combination. A third assumption, made in the fin problem, was that the heat transfer at the far end can be neglected. The solution including this effect, where $h_L L/k$ is an axial Biot number is given as Equation (18.19). If the quantity $h_L L/k$ is small, you can see that Equation (18.19) reduces to the previous result (18.13).

$$\frac{T-T_\infty}{T_0-T_\infty} = \frac{\cosh(mL(1-\xi)) + (\text... ...axial}/m)\sinh(mL(1-\xi))} {\cosh(mL)+(\textrm{Bi}_\textrm{axial}/mL)\sinh(mL)}$$ (18..19)

and

$$\frac{\dot{Q}}{\sqrt{kAhP}(T_0-T_\infty)} = \cfrac{\textrm{Bi}_\textrm{axial}/mL+ \tanh(mL)} {1+\cfrac{\textrm{Bi}_\textrm{axial}}{mL}\tanh(mL)}.$$ (18..20)