19.2 Kirchhoff's Law and ``Real Bodies''
Real bodies radiate less effectively than black bodies. The
measurement of this is the emittance,
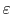 , defined by
, defined by
where 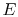 is radiation from the real body at
is radiation from the real body at  , and
, and 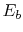 is
radiation from a black body at
is
radiation from a black body at  .
.
Values of emittance vary greatly for different materials. They are
near unity for rough surfaces such as ceramics or oxidized metals,
and roughly 0.02 for polished metals or silvered reflectors. A table
of emittances for different substances is given at the end of this
section as Table 19.1, taken from the book by
Lienhard.
The level of the emittance can be related to the absorptance using
the following arguments. Suppose we have a small non-black body in
the cavity. The power absorbed per unit area is equal to 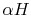 .
The power emitted is equal to
.
The power emitted is equal to 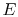 . An energy balance gives
. An energy balance gives
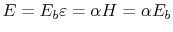 . Thus
. Thus
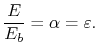 |
(19..1) |
Equation (19.1), the relation
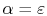 , is known as Kirchhoff's Law. It implies that good
radiators are good absorbers. It was derived for the case when
, is known as Kirchhoff's Law. It implies that good
radiators are good absorbers. It was derived for the case when
 and is not
strictly true for all circumstances when the temperature of the body
and the cavity are different, but it is true if
and is not
strictly true for all circumstances when the temperature of the body
and the cavity are different, but it is true if
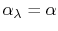 ,
,
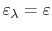 , so the absorptance and
emittance are not functions of
, so the absorptance and
emittance are not functions of 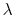 . This situation describes a
``gray body.'' Also, since
. This situation describes a
``gray body.'' Also, since
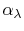 ,
,
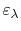 are properties of the surface,
are properties of the surface,
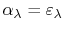 .
.
UnifiedTP
|

