

|
|
| Thermodynamics and Propulsion | |
Subsections
19.3 Radiation Heat Transfer Between Planar Surfaces
Consider the two infinite gray surfaces shown in
Figure 19.5. We suppose that the
surfaces are thick enough so that
The same can be said for a photon emitted from Surface 2:
We can add up all the energy
This is equal to
However
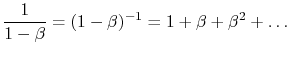
We thus observe that the radiation absorbed by surface 1 can be written as
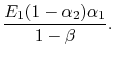
Likewise
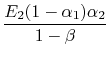
is the radiation generated at 2 and absorbed there as well. Putting this all together we find that
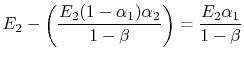
is absorbed by 1. The net heat flux from 1 to 2 is
If

If body 2 is black,
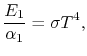
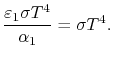
Therefore, again, Using Kirchhoff's Law we find,
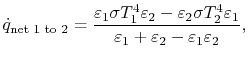
or, as the final expression for heat transfer between gray, planar, surfaces,
19.3.1 Example 1: Use of a thermos bottle to reduce heat transfer
For the same
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
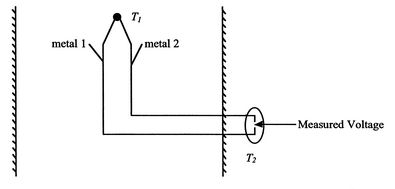
Thermocouples (see Figure 19.7) are commonly used to measure temperature. There can be errors due to heat transfer by radiation. Consider a black thermocouple in a chamber with black walls.
Suppose the air is at
![]() , the walls are at
, the walls are at
![]() , and the convective heat transfer coefficient
is
, and the convective heat transfer coefficient
is
![]() .
.
What temperature does the thermocouple read?
We use a heat (energy) balance on the control surface shown in Figure 19.8. The heat balance states that heat convected away is equal to heat radiated into the thermocouple in steady state. (Conduction heat transfer along the thermocouple wires is neglected here, although it would be included for accurate measurements.)
The heat balance is
where
from which we find
Muddy Points
Which bodies does the radiation heat transfer occur between in the thermocouple?(MP 19.1)
Still muddy about thermocouples. (MP 19.2)
Why does increasing the local flow velocity decrease the temperature error for the thermocouple? (MP 19.3)
UnifiedTP