6.1 Limitations on the Work that Can be Supplied by a Heat Engine
The second law enables us to make
powerful and general statements concerning the maximum work that can
be derived from any heat engine which operates in a cycle. To
illustrate these ideas, we use a Carnot cycle which is shown
schematically in Figure 6.1.
Figure 6.1:
A Carnot cycle heat engine
|
|
The engine operates between two heat reservoirs, exchanging heat
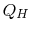 with the high temperature reservoir at
with the high temperature reservoir at 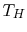 and
and 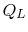 with
the reservoir at
with
the reservoir at 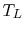 . The entropy changes of the two reservoirs
are
. The entropy changes of the two reservoirs
are
The same heat exchanges apply to the system, but with opposite
signs: the heat received from the high temperature source is
positive, and conversely. Denoting the heat transferred to the
engines by subscript ``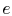 '',
'',
The total entropy change during any operation of the engine is
For a cyclic process, the third of these (
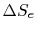 )is zero, and thus (remembering that
)is zero, and thus (remembering that 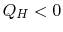 ),
),
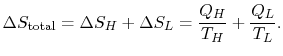 |
(6..1) |
For the engine we can write the first law as
Or,
Hence, using (6.1)
The work of the engine can be expressed in terms of the heat received by the engine as
The upper limit of work that can be done occurs during a reversible
cycle, for which the total entropy change (
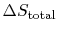 ) is zero. In this situation:
) is zero. In this situation:
Also, for a
reversible cycle of the engine,
These constraints apply to all reversible heat engines
operating between fixed temperatures. The thermal efficiency of the
engine is
The Carnot efficiency is thus the maximum efficiency that can occur
in an engine working between two given temperatures.
We can approach this last point in another way. The engine work is
given by
or,
The total entropy change can be written in terms of the Carnot cycle
efficiency and the ratio of the work done to the heat absorbed by
the engine. The latter is the efficiency of any cycle we can devise:
The second law says that the total entropy
change is equal to or greater than zero. This means that the Carnot
cycle efficiency is equal to or greater than the efficiency for any
other cycle, with the total equality only occurring if
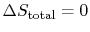 .
.
Muddy Points
So, do we lose the capability to do work when we have an
irreversible process and entropy increases?
(MP 6.1)
Why do we study cycles starting with the Carnot cycle? Is it because
it is easier to work with?
(MP 6.2)
UnifiedTP
|


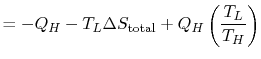
![$\displaystyle =-Q_H\left[1-\left(\frac{T_L}{T_H}\right)\right]-T_L\Delta S_\textrm{total}.$](img642.png)
![$\displaystyle W_e=Q_{He}\left[1-\left(\frac{T_L}{T_H}\right)\right]-T_L\Delta S_\textrm{total}.$](img643.png)
![$\displaystyle \textrm{Maximum work for an engine working between $T_H$ and
$T_L$:}\quad W_e
=Q_{He}\left[1-\left(\frac{T_L}{T_H}\right)\right].$](img645.png)
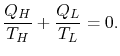
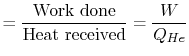
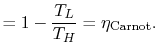
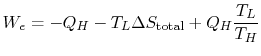
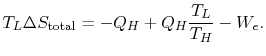
![$\displaystyle \Delta S_\textrm{total} = \frac{Q_{He}}{T_L}\left[1-\frac{T_L}{T_...
...c{Q_{He}}{T_L}\biggl[\eta_\textrm{Carnot}-\eta_\textrm{Any
other cycle}\biggr].$](img652.png)