6.2 The Thermodynamic Temperature Scale
The considerations of Carnot cycles in this section have not
mentioned the working medium. They are thus not limited to an ideal
gas and hold for Carnot cycles with any medium. Earlier we derived
the Carnot efficiency with an ideal gas as a medium and the
temperature definition used in the ideal gas equation was not
essential to the thermodynamic arguments. More specifically, we can
define a thermodynamic temperature scale that is independent of the
working medium. To see this, consider the situation shown below in
Figure 6.2, which has three reversible
cycles. There is a high temperature heat reservoir at 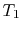 and a
low temperature heat reservoir at
and a
low temperature heat reservoir at 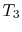 . For any two temperatures
. For any two temperatures
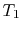 ,
, 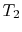 , the ratio of the magnitudes of the heat absorbed and
rejected in a Carnot cycle has the same value for all systems.
, the ratio of the magnitudes of the heat absorbed and
rejected in a Carnot cycle has the same value for all systems.
Figure 6.2:
Arrangement of heat engines
to demonstrate the thermodynamic temperature scale
|
|
We choose the cycles so 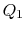 is the same for A and C. Also
is the same for A and C. Also 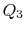 is
the same for B and C. For a Carnot cycle
is
the same for B and C. For a Carnot cycle
Also
But
Hence
We thus conclude that
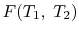 has the form
has the form
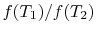 ,
and similarly
,
and similarly
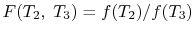 . The ratio of the heat
exchanged is therefore
. The ratio of the heat
exchanged is therefore
In general,
so that the ratio of the heat exchanged is a function of the
temperature. We could choose any function that is monotonic, and one
choice is the simplest: 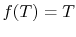 . This is the thermodynamic scale of
temperature,
. This is the thermodynamic scale of
temperature,
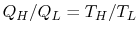 . The temperature defined in this
manner is the same as that for the ideal gas; the thermodynamic
temperature scale and the ideal gas scale are equivalent.
. The temperature defined in this
manner is the same as that for the ideal gas; the thermodynamic
temperature scale and the ideal gas scale are equivalent.
UnifiedTP
|

