8.2 Work and Heat Transfer with Two-Phase Media
We examine the work and heat transfer in quasi-static processes with
two-phase systems. For definiteness, consider the system to be a
liquid-vapor mixture in a container whose volume can be varied
through movement of a piston, as shown in
Figure 8.6. The system is kept at constant
temperature through contact with a heat reservoir at temperature
 . The pressure is thus also constant, but the volume,
. The pressure is thus also constant, but the volume, 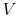 , can
change. For a fixed mass, the volume is proportional to the specific
volume
, can
change. For a fixed mass, the volume is proportional to the specific
volume
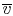 so that point
so that point 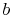 in
Figure 8.6 must move to the left or the right as
in
Figure 8.6 must move to the left or the right as
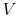 changes. This implies that the amount of mass in each of the two
phases, and hence the quality, also changes because mass is
transferred from one phase to the other. We wish to find the heat
and work transfer associated with the change in mass in each phase.
The change in volume can be related to the changes in mass in the
two phases as,
changes. This implies that the amount of mass in each of the two
phases, and hence the quality, also changes because mass is
transferred from one phase to the other. We wish to find the heat
and work transfer associated with the change in mass in each phase.
The change in volume can be related to the changes in mass in the
two phases as,
The system mass is constant
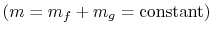 so
that for any changes
so
that for any changes
We can define the quantity
In terms of 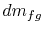 the
volume change of the system is
the
volume change of the system is
The work done is given by
The change in internal energy, 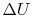 ,
can be found as follows. The internal energy of the system can be
expressed in terms of the mass in each phase and the specific
internal energy (internal energy per unit mass,
,
can be found as follows. The internal energy of the system can be
expressed in terms of the mass in each phase and the specific
internal energy (internal energy per unit mass, 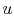 ) of the phase
as,
) of the phase
as,
Note that the
specific internal energy of the two-phase system can be expressed in
a similar way as the specific volume in terms of the quality and the
specific internal energy of each phase:
Writing the first law for this process:
The heat needed for the transfer of mass is proportional to the
difference in specific enthalpy between vapor and liquid. The
pressure and temperature are constant, so that the specific internal
energy and the specific enthalpy for the liquid phase and the gas
phase are also constant. For a finite change in mass from liquid to
vapor, 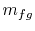 , therefore, the quantity of heat needed is
, therefore, the quantity of heat needed is
The heat needed per unit mass, 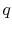 , for transformation between the
two phases is
, for transformation between the
two phases is
The notation 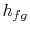 refers to the specific enthalpy change between
the liquid state and the vapor state. The expression for the amount
of heat needed,
refers to the specific enthalpy change between
the liquid state and the vapor state. The expression for the amount
of heat needed, 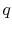 , is a particular case of the general result that
in any reversible process at constant pressure, the heat flowing
into, or out of, the system is equal to the enthalpy change. Heat is
absorbed if the change is from solid to liquid (heat of fusion),
liquid to vapor (heat of vaporization), or solid to vapor (heat of
sublimation).
, is a particular case of the general result that
in any reversible process at constant pressure, the heat flowing
into, or out of, the system is equal to the enthalpy change. Heat is
absorbed if the change is from solid to liquid (heat of fusion),
liquid to vapor (heat of vaporization), or solid to vapor (heat of
sublimation).
A numerical example is furnished by the vaporization of water at
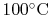 :
:
- How much heat is needed per unit mass of fluid vaporized?
- How much work is done per unit mass of fluid vaporized?
- What is the change in internal energy per unit mass of fluid vaporized?
In addressing these questions, we make use of the fact that problems
involving heat and work exchanges in two-phase media are important
enough that the values of the specific thermodynamic properties that
characterize these transformations have been computed for many
different working fluids. The values are given in SB&VW in Tables
B.1.1 and B.1.2 for water at saturated conditions and in Tables
B.1.3, B.1.4, and B.1.5 for other conditions, as well as for other
working fluids, as well as in the Appendix. From these, for water:
- At
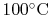 , the vapor pressure is
, the vapor pressure is
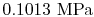 .
.
- The specific enthalpy of the vapor,
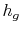 , is
, is
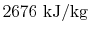 and the specific enthalpy of the liquid,
and the specific enthalpy of the liquid, 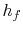 , is
, is
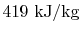 .
.
- The difference in enthalpy between liquid and
vapor,
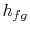 , occurs often enough so that it is tabulated also.
This is
, occurs often enough so that it is tabulated also.
This is
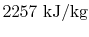 .
.
- The specific volume of the vapor is
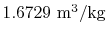 and the specific volume of the
liquid is
and the specific volume of the
liquid is
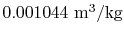 .
.
The heat input to the system is the change in enthalpy between
liquid and vapor, 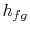 , and is equal to
, and is equal to
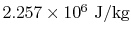 .
.
The work done is
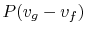 which has a value of
which has a value of
The change in internal energy per unit mass 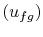 can be found
from
can be found
from
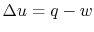 or from the tabulated values as
or from the tabulated values as
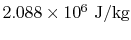 . This is much larger than the work done. Most of
the heat input is used to change the internal energy rather than
appearing as work.
. This is much larger than the work done. Most of
the heat input is used to change the internal energy rather than
appearing as work.
Muddy Points
For the vapor dome, is there vapor and liquid inside the dome and
outside is it just liquid or just gas? Is it interchangeable? Is it
true for the plasma phase?
(MP 8.1)
What is 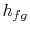 ? How do we find it? (MP 8.2)
? How do we find it? (MP 8.2)
Reasoning behind the slopes for
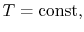 lines in the
lines in the
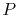 -
-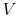 diagram. (MP 8.3)
diagram. (MP 8.3)
For a constant pressure heat addition, why is
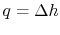 ?
(MP 8.4)
?
(MP 8.4)
What is latent heat? (MP 8.5)
Why is 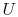 a function of
a function of 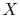 ? (MP 8.6)
? (MP 8.6)
UnifiedTP
|


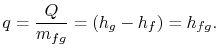
![]() :
:
![]() , and is equal to
, and is equal to
![]() .
.
![]() which has a value of
which has a value of
![]() can be found
from
can be found
from
![]() or from the tabulated values as
or from the tabulated values as
![]() . This is much larger than the work done. Most of
the heat input is used to change the internal energy rather than
appearing as work.
. This is much larger than the work done. Most of
the heat input is used to change the internal energy rather than
appearing as work.
![]() ? How do we find it? (MP 8.2)
? How do we find it? (MP 8.2)
![]() lines in the
lines in the
![]() -
-![]() diagram. (MP 8.3)
diagram. (MP 8.3)
![]() ?
(MP 8.4)
?
(MP 8.4)
![]() a function of
a function of ![]() ? (MP 8.6)
? (MP 8.6)