Thermodynamics and Propulsion

8.9 Muddiest Points on Chapter 8

MP 8..1   For the vapor dome, is there vapor and liquid inside the dome and outside is it just liquid or just gas? Is it interchangeable? Is it true for the plasma phase?

The vapor dome separates the two-phase region from the single-phase region. Inside, we have a mixture of liquid and vapor. The peak of the vapor dome is called the critical point. The left-hand side leg of the vapor dome (from the critical point) is called the saturated liquid line along which the quality $X$ is zero (purely liquid). The right-hand side leg is denoted the saturated vapor line and the quality $X$ is one (purely vapor). For further details see the notes.

Heating of a solid or liquid substance leads to phase transition to a liquid or gaseous state, respectively. This takes place at a constant temperature for a given pressure, and requires an amount of energy known as latent heat. On the other hand, the transition from a gas to an ionized gas, i.e., plasma, is not a phase transition, since it occurs gradually with increasing temperature. During the process, a molecular gas dissociates first into an atomic gas which, with increasing temperature, is ionized. The resulting plasma consists of a mixture of neutral particles, positive ions (atoms or molecules that have lost one or more electrons), and negative electrons.

MP 8..2   What is $h_{fg}$ ? How do we find it?

The quantity $h_{fg}$ represents the specific enthalpy change between the liquid and vapor phases of a substance at constant temperature, and thus constant pressure. It is therefore the heat input, per unit mass, to vaporize a kilogram of liquid. See notes, Section 8.2.

MP 8..3   Reasoning behind the slopes for $T=\textrm{const.}$ lines in the $P$ -$V$ diagram.

The slope of an isotherm in the gaseous phase (to the right of the vapor dome) is similar to the slope we found for the isotherm of an ideal gas $(PV=\textrm{const})$ . Inside the vapor dome pressure and temperature are directly related to one another ($P=P(T)$ , vapor pressure curve) such that an isotherm is a horizontal line (isobar inside the vapor dome). In the liquid phase the isotherms are very steep lines, because for liquids the volume is about constant (very low compressibility).

MP 8..4   For a constant pressure heat addition, why is $q=\Delta h$ ?

The combined first and second law is $dh = Tds + vdP$ . For a reversible constant pressure process, $dP=0$ , and the heat input, $dq$ , is $TdS$ . Thus for a reversible constant pressure process, $dq = dh$ .

For an irreversible process we can say from the steady flow energy equation: $dq = dh_t = dh + cdc$ . For a steady flow, the one-dimensional momentum equation is

$$cdc = -\frac{dP}{\rho} +\frac{F_\textrm{viscous}}{\rho},$$

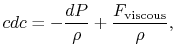
where $F_\textrm{viscous}$ represents the viscous forces in an irreversible flow. Combining these two expressions, and using $dP=0$ (the condition of constant pressure) gives

$$dq =dh +cdc =dh + \frac{F_\textrm{viscous}}{\rho}.$$

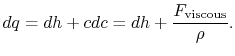
Without going into any detail concerning the form of the viscous forces, this equation shows that the equality between heat input and enthalpy change does not hold for general irreversible flow processes at constant pressure.

MP 8..5   What is latent heat?

Latent heat is a term for the enthalpy change needed for vaporization.

MP 8..6   Why is $U$ a function of $X$ ?

Inside the vapor dome we have a mixture of liquid and vapor. The internal energy $U$ of the system (liquid and vapor) can be expressed in terms of the mass in each phase and the specific internal energy $u$ of each phase as,

$$U = u_f m_f + u_g m_g.$$

Introducing the quality $X$ as the fraction of the total mass in the vapor phase, $X = m_g/(m_g+m_f)$ , we can write

$$U = m [(1 - X) u_f + X u_g].$$

Since the specific energy of the saturated liquid and the saturated vapor are functions of temperature the internal energy $U$ of the two-phase system is a function of $X$ and $T$ (see also notes Section 8.2).

MP 8..7   What is the reason for studying two-phase cycles?

We study them because of their immense practical utility in a number of industrial devices and their intrinsic interest as applications of the basic principles.

MP 8..8   How did you get thermal efficiency? How does a boiler work?

The thermal efficiency is, as previously, the net work done divided by the heat input. Using the first law for a control volume we can write both of these quantities in terms of the enthalpy at different states of the cycle.

For the steam cycles discussed in class, a boiler is a large (as in the viewgraph of the Mitsubishi power plant) structure with a lot of tubes running through it. The water (or whatever medium is used in the cycle) runs through the tubes. Hot gases wash over the outside of the tubes. The hot gases could be from a combustor or from the exit of a gas turbine.

MP 8..9   Where does degrees Rankine come from? Related to Rankine cycles?

I think the answer is yes, although I do not know for sure. If so, this is the same Rankine who has his name on the Rankine-Hugoniot conditions across a shock wave.

MP 8..10   Why do we look at the ratio of pump (compression) work to turbine work? We did not do that for the Brayton cycle.

If the ratio of compression work to turbine work were close to unity for an ideal cycle, small changes in component efficiencies would have large effects on cycle efficiency and work. For the Rankine cycle this is not true. (The effect of pump efficiency on Rankine cycle efficiency is clearly small in the class example.) For the Brayton cycle, where the net work is the difference of two numbers which are of (relatively) similar sizes, the effect of compressor and turbine efficiency on cycle efficiency can be much larger.

I used the word ``sensitive'' and the meaning was that the cycle performance responded strongly to changes in the compressor and turbine behavior.

MP 8..11   Shouldn't the efficiency of the super/re-heated Rankine cycle be larger because its area is greater?

The area enclosed by an ideal cycle in a $T$ -$s$ diagram is the net work done, but it does not tell you about efficiency. We saw that for example when we looked at the Brayton cycle for the condition of maximum work, rather than maximum efficiency (see Section 3.7.2).

MP 8..12   Why can't we harness the energy in the warm water after condensing the steam in a power plant?

Let's assume the temperature of the warm water after condensing the steam is at a temperature of about 30 to 40 degrees C. If we consider running a heat engine between this heat reservoir (say 35 degrees C) and the surroundings at 20 degrees C, we would get an ideal thermal efficiency of about 5%. In other words, the available useful work is relatively small if we considered the lower heat reservoir to be the surroundings. In general, there is a property that only depends on state variables called availability. The change in availability gives the maximum work between two states, where one state is referred to the surroundings (dead state).

Figure 8.21: An industrial $T$ -$s$ diagram

Figure 8.22: Clausius-Clapeyron Experimental Proof (3) [Burton Corblin North America]