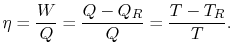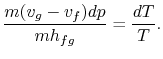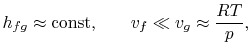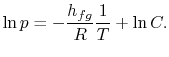8.4 The Clausius-Clapeyron Equation (application of
1st and 2nd laws of
thermodynamics)
Until now we have only considered ideal gases and we would like to
show that the properties 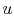 ,
, 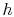 ,
, 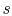 , etc. are true state
variables and that the 1st and
2nd laws of thermodynamics hold when the working
medium is not an ideal gas (i.e. a two-phase medium). An elegant
way to do this is to consider a Carnot cycle for a two-phase medium.
To state the fact that all Carnot engines operated between two given
temperatures have the same efficiency is one way of stating the
2nd law of thermodynamics. The working fluid need
not be an ideal gas and may be a two-phase medium changing phases.
, etc. are true state
variables and that the 1st and
2nd laws of thermodynamics hold when the working
medium is not an ideal gas (i.e. a two-phase medium). An elegant
way to do this is to consider a Carnot cycle for a two-phase medium.
To state the fact that all Carnot engines operated between two given
temperatures have the same efficiency is one way of stating the
2nd law of thermodynamics. The working fluid need
not be an ideal gas and may be a two-phase medium changing phases.
The idea is to run a Carnot engine between temperatures  and
and
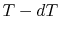 for a two-phase medium and to let it undergo a change in
phase. We can then derive an important relation known as the
Clausius-Clapeyron equation, which gives the slope of the
vapor pressure curve. We could then measure the vapor pressure
curve for various substances and compare the measured slope to the
Clausius-Clapeyron equation. This can then be viewed as an
experimental proof of the general validity of the
1st and 2nd laws of
thermodynamics!
for a two-phase medium and to let it undergo a change in
phase. We can then derive an important relation known as the
Clausius-Clapeyron equation, which gives the slope of the
vapor pressure curve. We could then measure the vapor pressure
curve for various substances and compare the measured slope to the
Clausius-Clapeyron equation. This can then be viewed as an
experimental proof of the general validity of the
1st and 2nd laws of
thermodynamics!
Figure 8.8:
Carnot cycle devised to test the validity of
the laws of thermodynamics
|
|
Consider the infinitesimal Carnot cycle 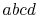 shown in
Figure 8.8. Heat is absorbed between states
shown in
Figure 8.8. Heat is absorbed between states
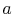 and
and 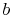 . To vaporize an arbitrary amount of mass,
. To vaporize an arbitrary amount of mass, 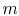 , the
amount of heat
, the
amount of heat
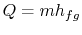 |
(8..1) |
must be supplied to the system. From the 1st and
2nd laws of thermodynamics the thermal efficiency
for a Carnot cycle can be written as
Hence, for the infinitesimal cycle considered above,
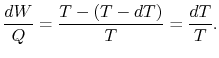 |
(8..2) |
The work along 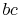 and
and 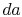 nearly cancel such that the net work is
the difference between the work along
nearly cancel such that the net work is
the difference between the work along 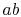 and
and 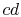 , and
, and 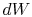 can be
viewed as the area enclosed by the rectangle
can be
viewed as the area enclosed by the rectangle  :
:
Substituting Equations (8.1) and
(8.3) into (8.2) one
obtains
Rearranging terms yields the Clausius-Clapeyron equation,
which defines the slope of the vapor pressure curve:
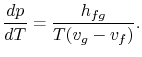 |
(8..4) |
The beauty is that we have found a general relation between
experimentally measurable quantities from first principles
(1st and 2nd laws of
thermodynamics).
In order to plot the Clausius-Clapeyron relation and to compare it
against experimentally measured vapor pressure curves, we need to
integrate Equation (8.4). To do so, the
heat of vaporization and the specific volumes must be known
functions of temperature. This is an important problem in physical
chemistry but we shall not pursue it further here except to mention
that if
- variations in heat of vaporization can be neglected,
- the vapor phase is assumed to be an ideal gas, and
- the specific volume of the liquid is small compared to that of
the vapor phase,
the integration can be readily carried out8.1. Making these approximations, the Clausius-Clapeyron
equation becomes
Carrying out the integration, the resulting expression is
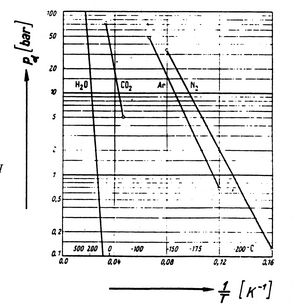
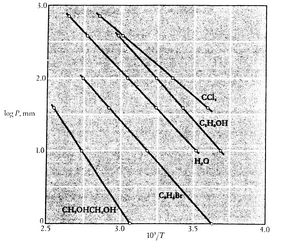
Note that the vapor pressure curves are straight lines if 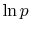 is
plotted versus
is
plotted versus 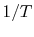 and that the slope of the curves is
and that the slope of the curves is
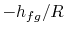 , directly related to the heat of vaporization.
Figures 8.9, 8.9, and
8.22 depict the vapor pressure curves for
various substances. The fact that all known substances in
the two-phase region fulfill the Clausius-Clapeyron equation
provides the general validity of the 1st and
2nd laws of thermodynamics!
, directly related to the heat of vaporization.
Figures 8.9, 8.9, and
8.22 depict the vapor pressure curves for
various substances. The fact that all known substances in
the two-phase region fulfill the Clausius-Clapeyron equation
provides the general validity of the 1st and
2nd laws of thermodynamics!
Figure 8.9:
Clausius-Clapeyron Experimental Proof
(1) [Gyarmathy, Thermodynamics I,
Eidgen
 ssische Technische Hochschule
Z
ssische Technische Hochschule
Z
 rich, 1992]
rich, 1992]
|
|
Figure 8.10:
Clausius-Clapeyron Experimental Proof
(2) [Mahan, Elementary Chemical Thermodynamics, 1963]
|
|
UnifiedTP
|