14.2 The Rocket Equation
We can now look at the role of specific impulse in setting the
performance of a rocket. A large fraction (typically 90%) of the
mass of a rocket is propellant, thus it is important to consider the
change in mass of the vehicle as it accelerates.
Figure 14.2:
Schematic for application of the momentum theorem.
|
|
There are several ways to do this through applying conservation of
momentum. Here we will apply the momentum theorem differentially by
considering a small mass, 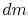 , expelled from the rocket during time
, expelled from the rocket during time
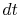 , Figure 14.2.
, Figure 14.2.
The initial momentum of the mass in the control volume (the vehicle)
is 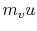 . The final momentum of mass in the control volume (the
vehicle and the mass expelled,
. The final momentum of mass in the control volume (the
vehicle and the mass expelled, 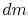 ) is
) is
The change in momentum during the interval 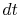 is
is
since 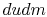 is a
higher order term. Now consider the forces acting on the system
which is composed of the masses
is a
higher order term. Now consider the forces acting on the system
which is composed of the masses 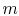 (the rocket), and
(the rocket), and 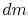 (the
small amount of propellant expelled from the rocket during time
(the
small amount of propellant expelled from the rocket during time
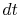 ):
):
Applying conservation of momentum, the resulting impulse, 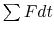 , must balance the change in momentum of the system:
, must balance the change in momentum of the system:
Then since
where 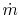 is the propellant mass flow rate, we have
is the propellant mass flow rate, we have
or, for 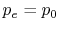 ,
,
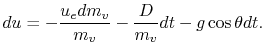 |
(14..1) |
Equation 14.1 is known as The Rocket Equation. It can be
integrated as a function of time to determine the velocity of the
rocket.
If we set
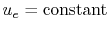 , assume that at
, assume that at 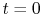 ,
, 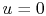 ,
neglect drag, and set
,
neglect drag, and set
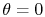 , then we can simplify the rocket
equation to
, then we can simplify the rocket
equation to
which can be integrated to give
where 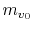 is the initial mass of the rocket. We can also write
this result as
is the initial mass of the rocket. We can also write
this result as
We can view this equation as being similar to the Breguet Range
Equation for aircraft. It presents the overall dependence of the
principal performance parameter for a rocket (velocity, 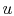 ), on the
efficiency of the propulsion system (Isp), and the structural design
(ratio of total mass to structural mass, since the initial mass is
the fuel mass plus the structural mass and the final mass is only
the structural mass).
), on the
efficiency of the propulsion system (Isp), and the structural design
(ratio of total mass to structural mass, since the initial mass is
the fuel mass plus the structural mass and the final mass is only
the structural mass).
Assuming the rate of fuel consumption is constant, the mass of the
rocket varies over time as
where 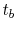 is the time at which all of the propellant is used. This
expression can be substituted into the equation for velocity and
then integrated to find the height at the end of burnout:
is the time at which all of the propellant is used. This
expression can be substituted into the equation for velocity and
then integrated to find the height at the end of burnout:
which for a single stage sounding rocket
with no drag and constant gravity yields
The final height of the rocket can then be determined by equating
the kinetic energy of the vehicle at burnout with its change in
potential energy between that point and the maximum height. This is
left as an exercise for the reader.
To conclude this section, Figure 14.3 shows the
most powerful rocket built, the NASA Saturn V rocket, which was used
during the Apollo program to reach the Moon.
Figure 14.3:
The Saturn V rocket stood 365 feet tall and had 5 stages.
It produced over 7.5 million pounds of thrust at liftoff (NASA,
1969).
|
|
UnifiedTP
|


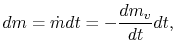
![]() , assume that at
, assume that at ![]() ,
, ![]() ,
neglect drag, and set
,
neglect drag, and set
![]() , then we can simplify the rocket
equation to
, then we can simplify the rocket
equation to
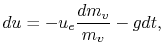
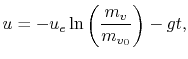
![$\displaystyle u = g \left[\textrm{Isp} \ln\left(\frac{m_{v_0}}{m_v}\right)-t\right].$](img1690.png)
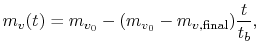
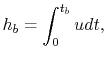
![$\displaystyle h_b = g \left[-t_b \textrm{Isp}\cfrac{\ln\left(\cfrac{m_{v_0}}{m_...
...}{m_{v,\textrm{final}}}-1\right)} + t_b \textrm{Isp} - \frac{1}{2}t_b^2\right].$](img1694.png)
