15.1 Fuels
There are a wide variety of fuels used for aerospace power and
propulsion. A primary one is jet fuel, essentially kerosene. Kerosene is a mixture of various hydrocarbons. The fuels we consider here are hydrogen (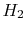 ), methane (
), methane (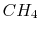 ), and octane (
), and octane (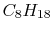 ). ).
The chemical process in which a fuel, for example methane, is burned
consists of (on a very basic level -— there are many intermediate
reactions that need to be accounted for when computations of the
combustion process are carried out):
The reactions we describe are carried out in air, which can be
approximated as 21% 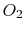 and 79%
and 79% 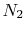 . This composition is
referred to as ``theoretical air.'' There are other components of
air (for example Argon, which is roughly 1%), but the results given
using the theoretical air approximation are more than adequate for
our purposes. With this definition, for each mole of
. This composition is
referred to as ``theoretical air.'' There are other components of
air (for example Argon, which is roughly 1%), but the results given
using the theoretical air approximation are more than adequate for
our purposes. With this definition, for each mole of 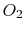 , 3.76 (or
, 3.76 (or
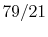 ) moles of
) moles of 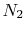 are involved:
are involved:
Even if the nitrogen is not part of the
combustion process, it leaves the combustion chamber at the same
temperature as the other products, and this change in state (change
in enthalpy) needs to be accounted for in the steady flow energy
equation. At the high temperatures achieved in internal combustion
engines (aircraft and automobile) reaction does occur between the
nitrogen and oxygen, which gives rise to oxides of nitrogen,
although we will not consider these reactions.
The condition at which the mixture of fuel and air is such that both
completely participate in the reaction is called stoichiometric. In
gas turbines, excess air is often used so that the temperatures of
the gas exiting the combustor is kept to within desired limits (see
Figures 3.20, 3.21, and
3.24(b) for data on these
limits.)
Muddy Points
Why is there 3.76 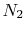 ? (MP 15.1)
? (MP 15.1)
What is the most effective way to solve for the number of moles in
the reactions? (MP 15.2)
UnifiedTP
|

